Rectas paralelas, como encontrarlas con Ejemplos
En este articulo se explicará como saber si 2 rectas son paralelas y como encontrar la recta paralela a una recta que pasa por un punto especifico
Como saber si dos rectas son paralelas
Cuando 2 rectas son paralelas estas tienen la característica que tienen la misma pendiente “m”, en cuanto a valor y dirección. Un aspecto importante entre 2 rectas paralelas es que estas no cortan en ningún momento entre sí, esto sucede porque las rectas siempre crecen al mismo ritmo por lo que no acortan distancias nunca.
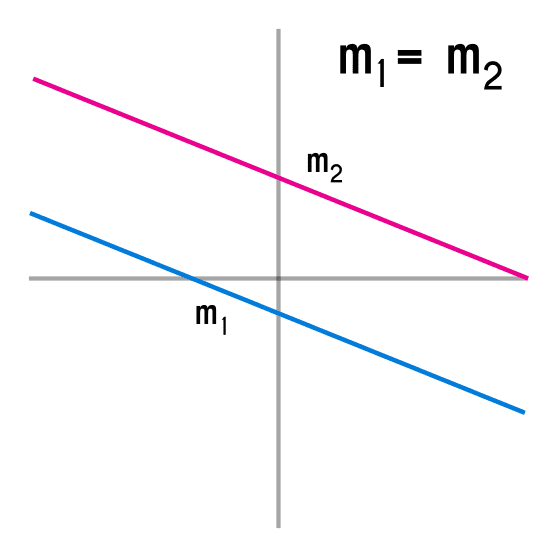
Entonces, sabiendo que estas tienen el mismo valor de la pendiente lo que se hace es comparar los valores de “m”, si las rectas se dan con la ecuación ordinaria “y = mx+b” es fácil, pues, lo único que se tiene que ver es que el numero que acompañan a las “x” sean los mismo en ambos casos y con el mismo signo, por ejemplo las rectas y=2x+4 y y= -2x-6 no son paralelas, porque una de estas pendientes es positiva y la otra es negativa, por lo que una es creciente y la otra es decreciente y estas si que cortan en algún momento dado, en cambio y=4x-5 y y=4x +12 sí que son paralelas porque las pendientes tienen el mismo signo y valor.
La cosa cambia un poco cuando las rectas se dan por la ecuación general, en este caso como no se puede apreciar el valor de “m” en la ecuación hay 2 formas de averiguarlo, la primer forma es pasando la ecuación a su forma ordinaria que se hace despejando “y”, y la otra manera es utilizando la siguiente formula para encontrar el valor de la pendiente (Recordatorio: la ecuación general de la recta es “ax + by + c = 0”).
- Encontrar pendiente
- m = -ab
Una vez calculadas las 2 pendientes de las rectas, simplemente se tiene que comparar si tienen el mismo valor y signo, Para comprender mejor se desarrollará el siguiente ejemplos: Comprobar si las rectas “10x – 2y + 4 = 0 “ y “5x – y + 2 = 0” son paralelas
- Se encuentra la pendiente de la primera recta
- m1 = -10-2
- m1 = 5
- Se encuentra la pendiente de la segunda recta
- m2 = -5-1
- m2 = 5
- por lo tanto
- m1 = m2
- Entonces son rectas paralelas
Encontrar una recta paralela teniendo un punto
Otro escenario que se puede dar es cuando se da la ecuación de una recta y se pide encontrar una recta paralela a esta que pasa por un punto (x,y) definido, para resolver esto lo primero que se tiene que hacer es encontrar la pendiente de la recta dada y luego plantear la ecuación punto-pendiente de la recta con la pendiente que de la primer recta (que va a ser la misma que la segunda) y el punto dado, luego simplemente se ordena la ecuación de la manera que se pide ya sea ordinaria o general.
- Ecuación punto pendiente
- y - y1 = m (x - x1)
Por ejemplo: Encontrar la recta paralela a y=3x+5 que pasa por el punto (0,2), en este caso ya se conoce la pendiente que es “3” por lo tanto se procede a plantear la ecuación punto pendiente.
- y - y1 = m (x - x1)
- y - 2 = 3 (x -0)
- Se resuelve y se despeja la "y"
- y - 2 = 3x
- y = 3x + 2
Ejemplos de rectas paralelas
Ejemplo 1: Encontrar la recta paralela a "-8x + 2y -4 = 0" que pasa por el punto (3,1)
- Se encuentra la pendiente de la recta
- m = -ab
- m = -(-8)2
- m = 82
- m = 4
- Ahora se encuentra la ecuacion de la otra recta
- y - y1 = m (x - x1)
- y - 1 = 4 (x - 3)
- Se resuelve y se pasa todo a un mismo lado (para que quede en la forma general que es como se dio la primera recta)
- y - 1 = 4x - 12
- 4x - y + 13 = 0
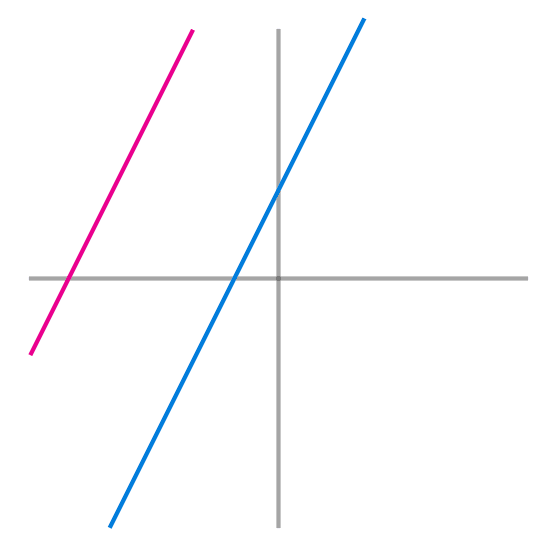
Ejemplo 2: Que recta paralela a "y=5x - 6" pasa por el punto (-2,5)
Como ya se tiene el valor de la pendiente m=5 simplemente se hacen los procedimientos en la ecuación punto pendiente
- Ahora se encuentra la ecuacion de la otra recta
- y - y1 = m (x - x1)
- y - 5 = 5 (x - (-2) )
- y - 5 = 5 (x +2 )
- Se resuelve y se despeja "y"
- y - 5 = 5x + 10
- y = 5x + 10 + 5
- y = 5x + 15
Artículos relacionados