Pendiente de una recta

En este artículo se mostrará que es la pendiente en una funcion lineal y como poder encontrarla a partir de dos puntos.

Qué es la pendiente de una recta

Cuándo se grafica una función lineal o función de primer grado, se obtiene una linea a la cual se le llama “recta”, este se caracteriza porque no esta no puede ser horizontal o vertical, sino que tiene esta está con cierta inclinación con respecto al eje “x”, y a esta inclinación que tiene la recta se le conoce como Pendiente de la recta. El valor de la pendiente de una recta se puede observar explícitamente en la forma de una función lineal: f(x)=mx+b, donde la variable que acompaña “x”, es decir “m”, es el valor de la pendiente de esa recta.

El valor de la letra “m” (la pendiente) indica que tanto avanza una recta y hacia donde avanza, por ejemplo si el signo de la pendiente “m” es positivo, la recta ira creciendo de izquierda a derecha, pero si la pendiente tiene signo negativo entonces esta ira decreciendo de izquierda a derecha en el plano cartesiano. Otra cosa que indica la pendiente es que tan inclinada es la recta, mientras mayor sea el valor de la pendiente, mayor será la inclinación de la recta con respecto al eje “x”, y mientras menor sea número de la pendiente, más aplanada será la recta.

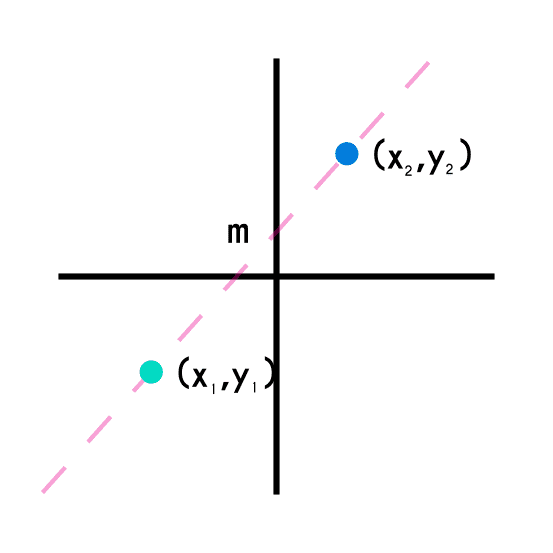
Como infuye el valor de la pendiente en una recta

El valor de “m” se interpreta de la siguiente manera: por cada “x” valores que la recta avance, esta avanzará “m” valores en “y”. Lo que indica esto es que por ejemplo, si se tiene una pendiente “m=4”, esto significa que la recta avanzará 4 valores en el eje “y” por cada 1 que avance en “x”.

En caso que el valor de la pendiente no sea un número entero sino que sea una fracción, entonces el crecimiento de la recta sera de la siguiente forma: teniendo una pendiente “m = a/b”, siendo “a” el numerador de la fracción (el número de arriba) y siendo “b” el denominador de la fracción (el número de abajo), entonces la recta cuya pendiente es igual a a/b avanzará “a” números en el eje “y” por cada “b” números en el eje “x”.

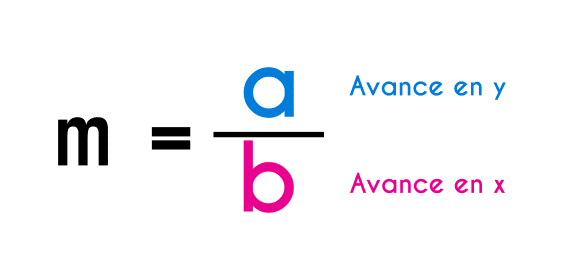
Esto quiere decir que si se tiene una pendiente igual a 3/5, entonces la recta avanzará 3 números en “y” por cada 5 en “x”.

Ahora conociendo que es una pendiente y como interpretarla, hay que saber como encontrarla. Cuando se plantea un problema donde halla que encontrar la pendiente de una recta por lo general se dan dos puntos (coordenadas (x,y) ) por donde pasa la función, entonces a partir de esto se puede utilizar la siguiente formula para definir el valor de la pendiente.

• Fórmula de la pendiente (m)
• m =
  Δy/Δx
• donde
• Δy = y₂ - y₁
• Δx = x₂ - x₁

Aclaración: cuando se van a introducir las coordenadas (x,y) en las fórmulas no importa el orden en el que se metan, por ejemplo, si se dan las coordenadas (2,4) y (4, 8) , no afecta en nada si se toma como y₁ =4 y y₂=8 ó viceversa, el resultado siempre será el mismo, eso sí, que hay que tener cuidado con las leyes de los signos, porque si se falla al operar con signos, la dirección o el signo de la pendiente puede estar erróneo.

Artículos relacionados