Ecuación punto-pendiente con ejemplos
En este articulo se desarrolarán ejemplos de las ecuaciones punto-pendiente y la manera correcta de usarlas.
La ecuación punto pendiente es una manera de representar una recta o función lineal, se llama de esta manera porque en la ecuación está explícitamente el punto donde corta la recta con el eje “y” y porque en ella también se puede ver el valor de la pendiente.
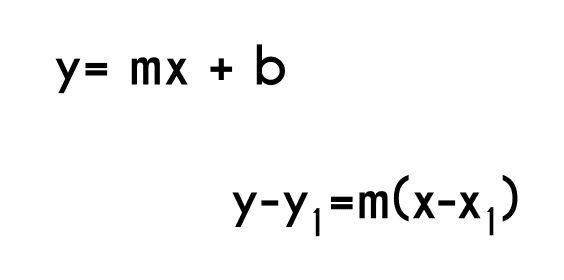
Antes de iniciar con más detalles hay que aclarar los conceptos de punto y pendiente: el punto de corte con el eje “y” es el punto exacto donde la recta pasa sobre el eje y, mientras que la pendiente define que tan inclinada será la grafica de la función, mientras mayor sea el valor de la pendiente, más inclinada estará la recta, también es importante el signo de la pendiente, si el signo de la pendiente es positivo, entonces la gráfica crecerá de izquierda a derecha y si la pendiente tiene un signo negativo, entonces la gráfica crecerá de derecha a izquierda.
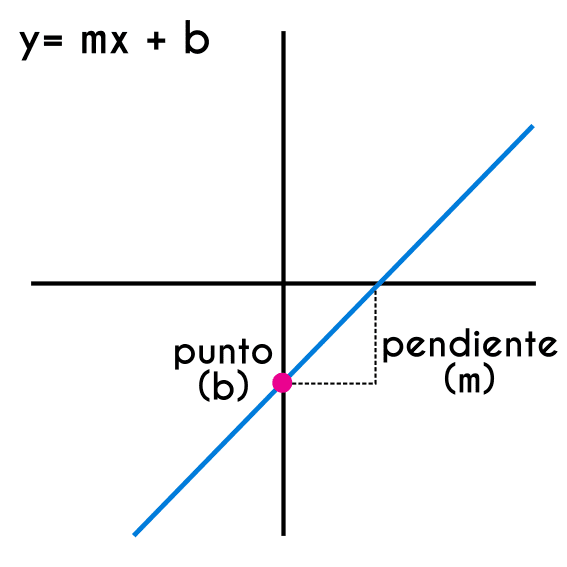
Hay 2 ecuaciones que se pueden conocer como punto-pendiente, una es la que tiene la forma y=mx+b, donde “m” es el valor de la pendiente y “b” es el punto de corte con el eje “y”, esta es la mas usada en otros temas como las funciones lineales, pero también hay otra ecuación y es la que tiene la forma y-y1 = m (x – x1), esta por lo general se utiliza para encontrar la primera ecuación, y es útil cuando se da la pendiente de la recta y un punto cualquiera por donde pasa la recta (por eso hay un "x1" y "y1" porque estas son las coordenadas del punto donde pasa la recta), para pasar de esta ecuación a la primera simplemente se resuelve el paréntesis y luego se despeja la “y”, ejemplos de esto más abajo.
Ejemplos de la ecuación punto pendiente
Los siguientes ejemplos serán acerca de como encontrar la ecuación punto pendiente conociendo la pendiente de una recta y un punto por donde pasa, utilizando la ecuación y-y1 = m (x – x1
Ejemplo 1: Encontrar la ecuación punto pendiente de una recta que tiene una pendiente igual a 3 y pasa por el punto (1,1)
- Primero se plantea la ecuación
- y-y1 = m (x – x1),
- Luego se sustituirá las variables m (pendiente) y "x1,y1" que es el punto por donde pasa la recta
- y-1 = 3 (x – 1)
- Lo primero que se hará es resolver el paréntesis
- y-1 = 3x - 3
- Ahora se deja la "y" sola en el lado izquierdo
- y = 3x - 3 + 1
- Y por último se resuevle el resto
- y = 3x - 3 + 1
- y = 3x - 2
Ejemplo 2: Cuál es la ecuacion punto pendiente de una recta cuyo m=-2 y pasa por (3,1)
- se plantea la ecuación
- y-y1 = m (x – x1),
- se sustituyen los valores
- y-1 = -2 (x – 3)
- Lo primero que se hará es resolver el paréntesis
- y-1 = -2x + 6
- Se despeja "y"
- y = -2x + 6 + 1
- Y por último se resuevle el resto
- y = -2x + 7
Ejemplo 3: Definir la ecuacion de la recta que pasa por el punto (-5,4) y tiene una pendiente igual a 2
- se plantea la ecuación
- y-y1 = m (x – x1),
- se sustituyen los valores
- y-4 = 2 (x – (-5) )
- se resuelve todo
- y-4 = 2 (x + 5 )
- y-4 = 2x + 10
- Se despeja "y"
- y = 2x + 10 + 4
- y = 2x + 14
Artículos relacionados