Encontrar los puntos de intersección entre dos Rectas, con Ejemplos
En este articulo Se mostrará como encontrar el punto donde cortan 2 rectas, con ejemplos paso a paso.
Corte entre 2 rectas
Siempre que haya dos rectas que no sean paralelas estas tendrán un punto de intersección en algún punto en el plano cartesiano, para saber si estas rectas son paralelas o no basta con mirar el valor de la pendiente, para ello primero hay que ordenar la ecuación de la recta de la forma y=mx+b, donde el valor de “m” es la pendiente, entonces, si el valor de la pendiente de ambas rectas es el mismo, entonces estas dos rectas no tienen un punto de intersección, si el valor de las pendientes tienen el mismo valor pero con signo diferente entonces estas si se interceptan
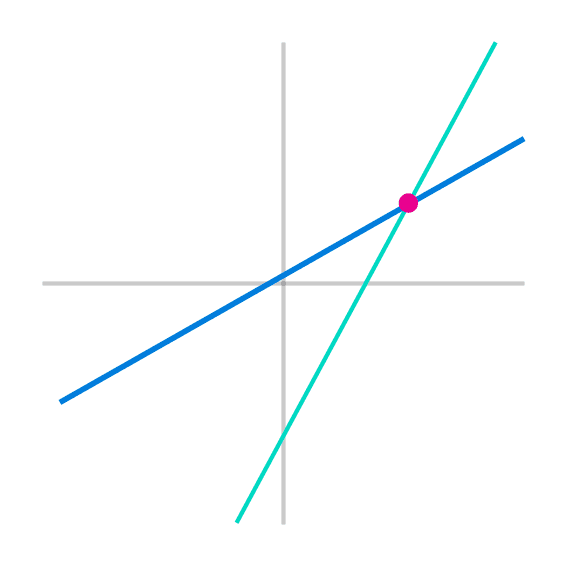
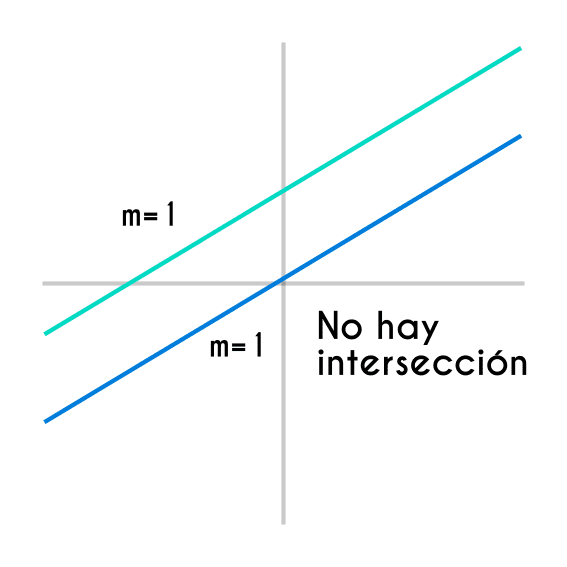
Una ves comprobado que dos rectas se interceptan entre sí, lo siguiente que hay que hacer es encontrar las coordenadas (x,y) donde esto sucede, para ello se forma un sistema de 2 ecuaciones con dos incógnitas que estará formada por las ecuaciones de las rectas, y hay que resolver este sistema de ecuaciones encontrando tanto el valor de “x” como el valor de “y”, y el resultado de estas 2 incógnitas será la coordenada en las que ambas rectas se intercepten.
Para resolver un sistema de ecuaciones con dos incógnitas existen tres métodos diferentes, pero el mas usado, por su facilidad es el método de sustitución, por lo tanto este será el método con los que se resolverán los ejemplos y ejercicios que se plantean más adelante.
Breve repaso del método de sustitución: este consiste en despejar cualquiera de las 2 variables de cualquiera de las dos ecuaciones y luego sustituir en la otra ecuación la variable por la ecuación que dio el despejar en la primera ecuación, con esto quedará una ecuación con una sola incógnita que se puede resolver, posteriormente se resuelve la ecuación y quedaría el primer dato de una de las variables, y este se sustituye en la primera ecuación que se despejó y de igual manera sé resuelve, y con esto ya se tienen los valores de ambas variables, Si esto no quedo claro, por favor ir a los ejemplos que están más abajo en este artículo para que se comprenda mejor lo que se acaba de explicar.
Ejemplos de punto de intersección entre 2 rectas
Ejemplo 1: Encontrar el punto de interseccion entre las rectas: 2x + 5y = 3 y 4x - 2y =18.
- 4x - 2y = 18
- Primero se despeja la variable "y" de la segunda ecuación
- -2y = 18 - 4x
- y =
-4x-218-2
- y = 2x - 9
- Ahora se reemplaza la ecuación de "y" en la otra ecuación
- 2x + 5y = 3
- 2x + 5(2x - 9) = 3
- Se resuelve el paréntesis y el resto de procesos
- 2x +10x - 45 = 3
- 12x - 45 = 3
- 12x = 3 + 45
- 12x = 48
- x = 4812
- x = 4
- Por útlimo se sustituye el valor de "x" en la primera ecuación que se despejo
- y = 2x - 9
- y = 2(4) - 9
- y = 8 - 9
- y = -1
- El punto de intesección entre estas dos rectas está en (4,-1)
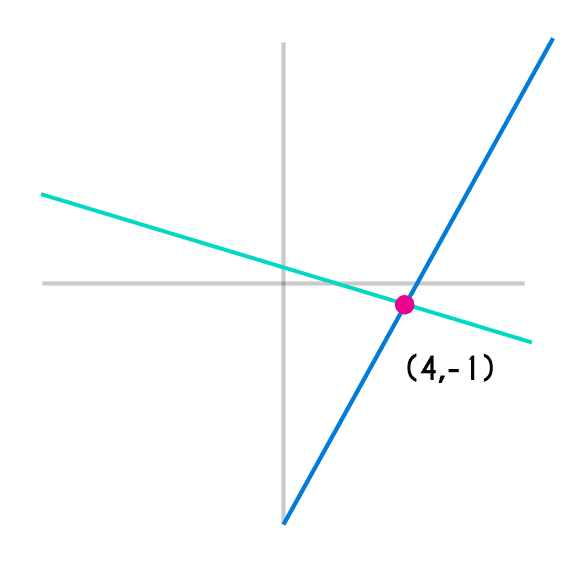
Ejemplo 2: hallar las coordenadas donde -4x + y = 8 y 8x + 2y = -16 cortan entre sí.
- Se despeja "y" de la primer ecuación
- -4x + y = 8
- y = 8 + 4x
- Se reemplaza "y" en la segunda ecuación
- 8x + 2(8 + 4x) = -16
- 8x + 16 + 8x = -16
- Se despeja "x"
- 8x + 16 + 8x = -16
- 16x = -16 -16
- 16x = -32
- x = -3216
- x = -2
- Y por último se sustituye "x" en la primer ecuación despejada
- y = 8 + 4x
- y = 8 + 4(-2)
- y = 8 - 8
- y = 0
- El punto de intesección entre estas dos rectas está en (-2,0)
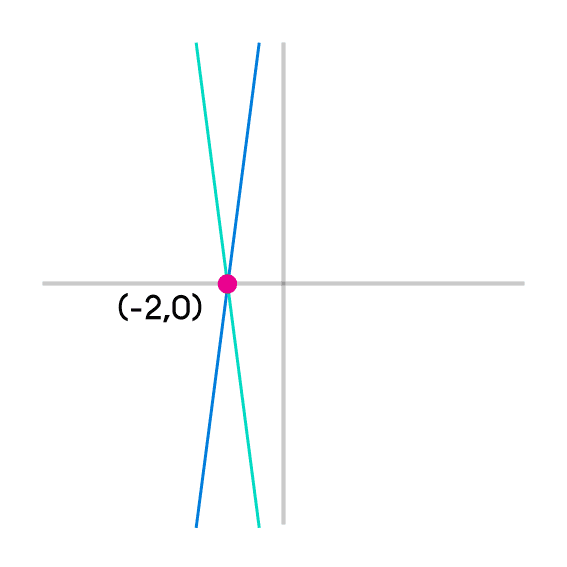
Ejemplo 3: encontrar las coordenadas (x,y) donde 2x + 6y = 6 y -5x + 9y = 9 se interceptan
- Se despeja "x" de la primer ecuación
- 2x + 6y = 6
- 2x = 6 - 6y
- 2x =
62-6y2
- x = 3 - 3y
- Se reemplaza "x" en la segunda ecuacion
- -5x + 9y = 9
- -5(3 - 3y) + 9y = 9
- -15 + 15y + 9y = 9
- 24y = 9 + 15
- 24y = 24
- y =
2424
- y = 1
- Ahora se cambia "y" en la ecuación que se despejo
- x = 3 - 3y
- x = 3 - 3(1)
- x = 3 - 3
- x = 0
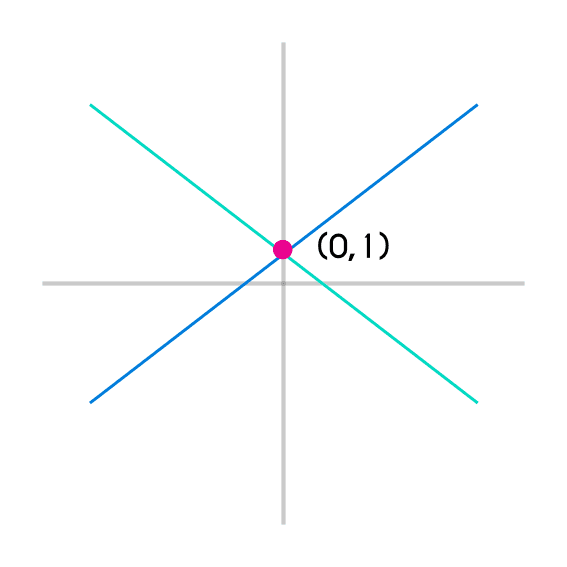
- El punto de intesección entre estas dos rectas está en (0,1)
Ejemplo 4: Calcular las coordenadas del punto de intersección entre 2x + 2y = 6 y 3x + y = 3
- Se despeja "y" de la segunda ecuación
- 3x + y = 3
- y = 3 - 3x
- Se reemplaza "y" en la primer ecuación
- 2x + 2y = 6
- 2x + 2(3 - 3x) = 6
- 2x + 6 - 6x = 6
- -4x = 6 - 6
- -4x = 0
- x =
0-4
- x = 0
- Ahora se cambia "x" en la ecuación que se despejó primero
- y = 3 - 3(0)
- y = 3 - 0
- y = 3
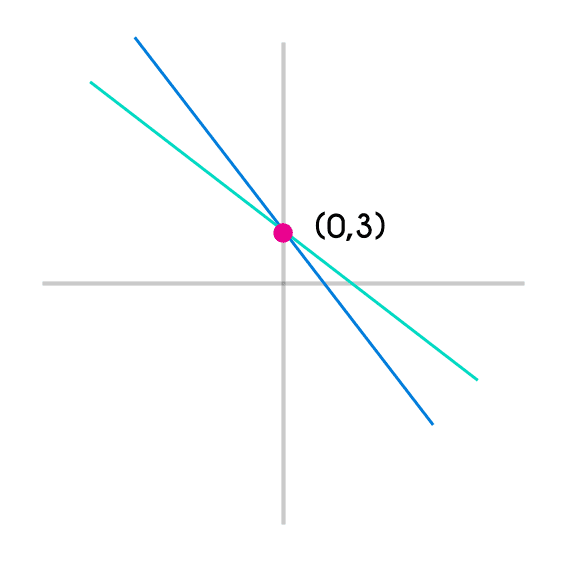
- El punto de intesección entre estas dos rectas está en (0,3)
Artículos relacionados