Cómo encontrar la ecuación general de una recta dados 2 puntos
En este articulo se hará una guia de como encontrar la ecuación de la recta conociendo 2 puntos por donde pasa
ax + bx + c = 0 es la forma o ecuación general, en otras ocasiones también llamada ecuación implícita de la recta, con ella se puede graficar la recta simplemente siguiendo ciertos procedimientos, pero también hay ocasiones en los que en lugar de dar una ecuación, se dan solamente 2 puntos y piden encontrar esta ecuación general de la recta a la que pertenezcan estos 2 puntos y esto es lo que se enseñará en este artículo.
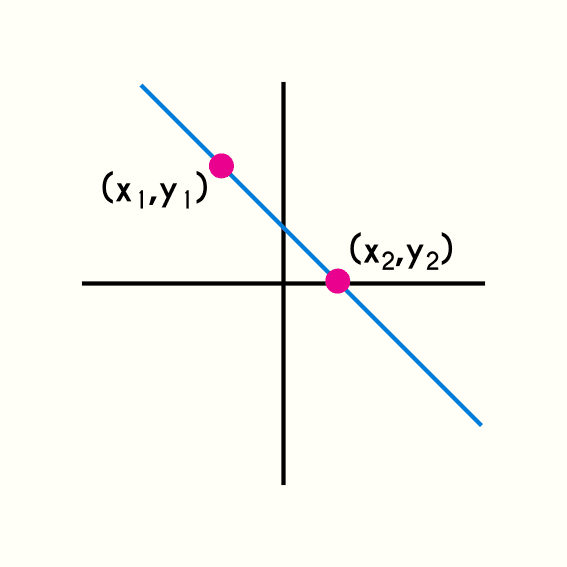
Pequeña aclaración: En realidad para poder graficar una recta basta con conocer dos puntos por donde pasa la recta, pero en ocasiones los puntos dados son muy distantes entre ellos y haría falta una gran precisión para graficarla de manera correcta en una plano cartesiano que sea de dimensiones pequeñas, por ejemplo si los puntos de la recta que se dan son (-500, 200) y (320, 400) esto se complicaría bastante de graficarlo en un plano de 10x10 o incluso menor, por este motivo es más conveniente saber la forma general de la función para luego graficar la recta a partir de ella.
Todo lo que se explica en los siguientes párrafos se desarrolla en los ejemplos que están más abajo.
Entonces, para encontrar la función general o implícita de una recta conociendo dos puntos lo que se hace es primero encontrar la pendiente de la recta, que como ya se conoce se obtiene con la siguiente fórmula
- Fórmula de la pendiente
- m = ΔyΔx
- ó
- m = y2 - y1x2 - x1
Cuando se ocupa esta fórmula en realidad no importa el orden en el que se pongan los puntos en la fórmula, es decir, que no importa cual punto se toma como punto 1 (x1, y1) o punto 2 (x2, y2), siempre que se apliquen bien las leyes de los signos no habrá problema.
Una vez conocida la pendiente de la recta, lo siguiente será utilizar la ecuación punto pendiente de la recta, que es de la siguiente manera:
- Ecuación punto-pendiente
- y - y1 = m (x - x1)
Como se puede ver aquí también hay un x1 y un y1, pues estas son las coordenadas (x,y) de un punto cualquiera de la recta, como ya se saben dos puntos por donde pasa la recta, se puede poner cualquiera de los 2 puntos en la ecuación esto no va a cambiar el resultado.
Una vez puesto las coordenadas en la ecuación punto pendiente, lo siguiente será resolver todo lo que se pueda (paréntesis o términos semejantes) y se pasa todo a un lado de la ecuación y con esto ya quedaría la ecuación general.
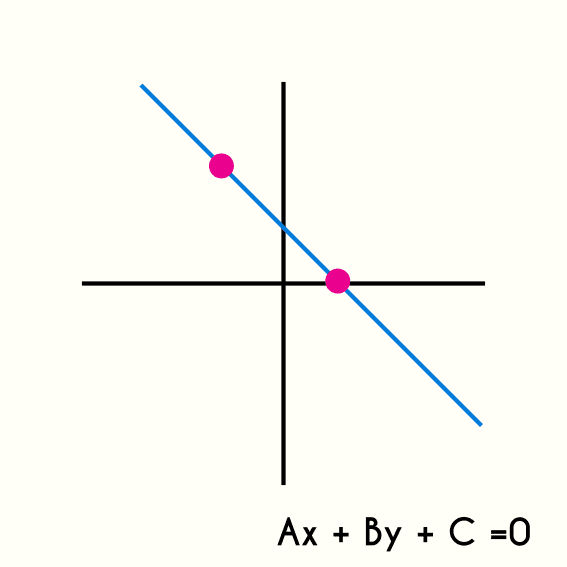
Ejemplos de encontrar ecuación general dados dos puntos
Ejemplo 1: Encontrar la ecuacion general de una recta que pasa por los puntos (2,1) y (3,3)
- Lo primero será encontrar la pendiente
- m = y2 - y1x2 - x1
- m = 3-13-2
- m = 21
- m = 2
- Ahora se plantea la ecuacion punto-pendiente
- y - y1 = m (x - x1)
- se cambia "m" por la pendiente y x1 y y1 por alguno de los 2 puntos
- en este caso se usará el primer punto (2,1)
- y - 1 = 2 (x - 2)
- se resuelve el parentésis
- y - 1 = 2x - 4
- se despeja todo a un solo lado y se iguala a 0
- y - 1 - 2x + 4 = 0
- se reducen terminos y se ordena la ecuacion
- -2x + y + 3 = 0
Ejemplo 2: Definir la ecuacion general de la recta que pasa por los puntos (5,0) y (10,10)
- Lo primero será encontrar la pendiente
- m = y2 - y1x2 - x1
- m = 10 - 010-5
- m = 105
- m = 2
- Ahora se plantea la ecuacion punto-pendiente
- y - y1 = m (x - x1)
- Se sustituye "m" y las coordenadas del primer punto
- y - 0 = 2 (x - 5)
- se resuelve el parentésis
- y - 0 = 2x - 10
- se despeja todo a un solo lado y se iguala a 0
- En este caso se pasa del lado izquierdo al derecho para que la "x" no quede negativa
- 2x - 10 - y = 0
Ejemplo 3:Cuál es la ecuacion de una recta que pasa por (3,-11) y (9,7)
- Lo primero será encontrar la pendiente
- m = y2 - y1x2 - x1
- m = 7-(-11)9-3
- m = 7+119-3
- m = 186
- m = 3
- Ahora se plantea la ecuacion punto-pendiente
- y - y1 = m (x - x1)
- Se sustituye "m" y las coordenadas del primer punto
- y - 7 = 3 (x - 9)
- se resuelve el parentésis
- y - 7 = 3x - 27 = 0
- se despeja todo a un solo lado y se iguala a 0
- 3x - y -27 + 7 = 0
- 3x - y -20 = 0
Artículos relacionados