Función logarítmica
En este articulo se mostrará el concepto en el que se basa un logaritmo y que es una función logarítmica
Para comprender todo lo que compone a una función logarítmica primero hay que aclarar el concepto de logaritmo. El resultado de un logaritmo es el exponente al cual se debe elevar un número denominado “base” para que este de como resultado un número en concreto.
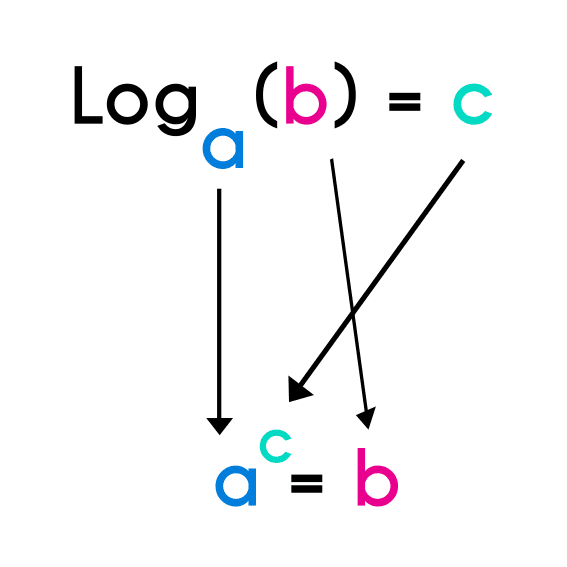
Definición de logarítmo
El logaritmo se escribe de la siguiente manera loga(b) = c, donde "a" es la base, “b” es el número que debe ser el resultado del exponente y “c” es el exponente al que se debe elevar la base "a" para que el resultado sea “c”, por ejemplo si se tiene el siguiente logaritmo: log2(3) entonces el dos es el número que se elevará y el 3 será el resultado que debe dar la operación, si este logaritmo se mete en una calculadora el resultado será log2(3) = 1.584962501, para comprobar si esto es cierto se hace la siguiente operación: 21.584962501, y el resultado es 3, por lo que el resultado arrojado por el logaritmo es correcto.
Ahora habiendo comprendido como funciona el logaritmo se puede proceder a la función logarítmica.
Se denomina una función logarítmica a una función donde la variable independiente “x” está en el lugar de “b” por ejemplo: f(x) = log2(x), pero esta función debe cumplir otras características o parámetros para que sea una función logarítmica valida.
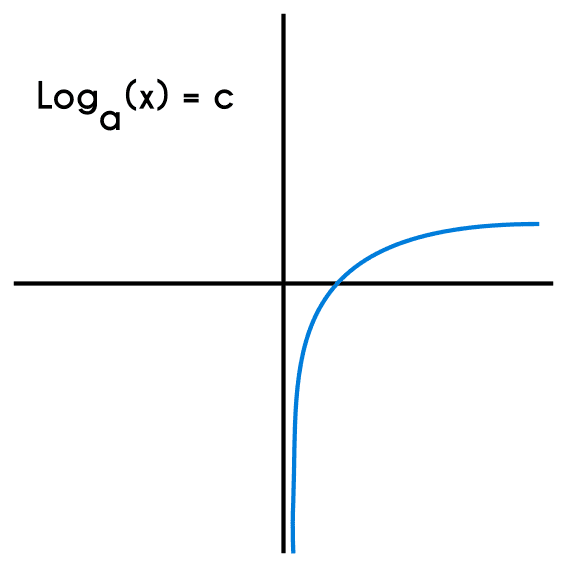
Propiedades de la función logarítmica
La base “a” no puede ser 0: cuando se eleva un 0 a cualquier número el resultado de este siempre va a ser 0, y hay que recordar que la variable “x” en un logaritmo es el resultado que da el elevar una base por un número, y como el único resultado que da un cero elevado a "c" (0c) es 0, el rango de la función se limitará a y=0, y esto se convertiría en una función constante y no en una función logrítmica.
La base “a” no puede ser 1: Algo parecido a lo anterior sucede cuando “a” es 1, y es que cuando la base de un exponente es 1, no importa a que número se esté elevando, la respuesta siempre será 1, por ejemplo 13 es igual a 1x1x1=1, o 15 es 1x1x1x1x1 = 1.
No hay “x” negativas: la “x” en un logaritmo es el resultado de elevar “a” al exponente “b” y no importa cuales valores tomen "a" o "b" el resultado será siempre un número positivo, por lo tanto el dominio de la función logarítmica general ( f(x) = loga(x)) son solo los reales positivo, pero esto puede cambiar cuando son funciones logarítmicas más complejas.
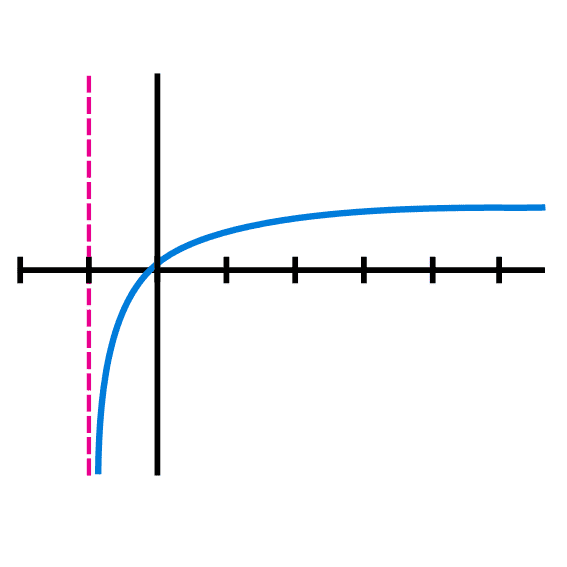
Asíntota de una función logarítmica
Como se puede observar en la gráfica de una función logarítmica, esta tiene una asíntota en el eje “x” que es la que marca el inicio del dominio de la función, esta, en la función logarítmica más simple, está en x=0, pero para encontrar esta asíntota en cualquier tipo de función logarítmica lo que se hace es igualar la ecuación que está en el lugar de “x” a 0 y despejar “x” y el resultado de esto será la posición de la asíntota.
Por ejemplo: encontrar la asíntota vertícal de la función f(x) = loga(2x+8)
- Primero se iguala la ecuación a 0
- 2x + 8 = 0
- Ahora se despeja "x"
- 2x = -8
- x =
-82
- x = -4
como el resultado fue x=-4, la asíntota de la función estará en -4, y en esta función el dominio no solo son los reales positivos, sino que el dominio de la función ira desde -4 hasta más infinito.
Ejemplos de función logarítmica
Ejemplo 1: Encontrar la posición de la asíntota de la función logarítmica f(x) = log10 (2x + 2).
- Se iguala la ecuación dentro del logarítmo a 0
- 2x + 2 = 0
- Ahora se despeja "x"
- 2x = -2
- x =
-22
- x = -1
Por lo tanto la asíntota de la función estará en x=-1.
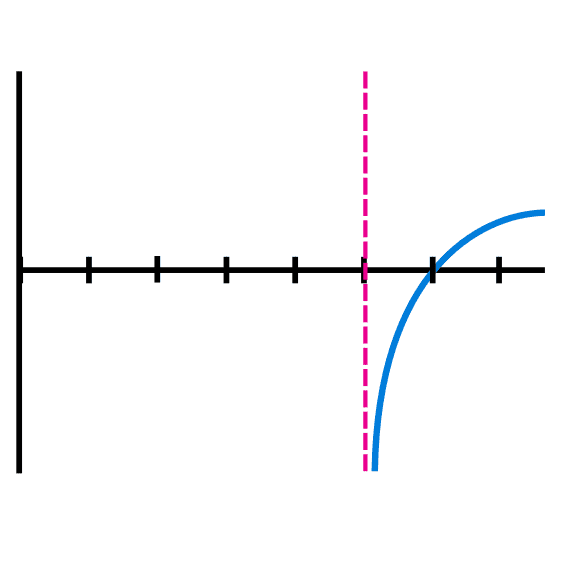
Ejemplo 2: Ubicar la posición de la asíntota de la función logarítmica f(x) = log2 (x-5).
- Se iguala la ecuación del logarítmo a 0
- x - 5 = 0
- Y se despeja "x"
- x = 5