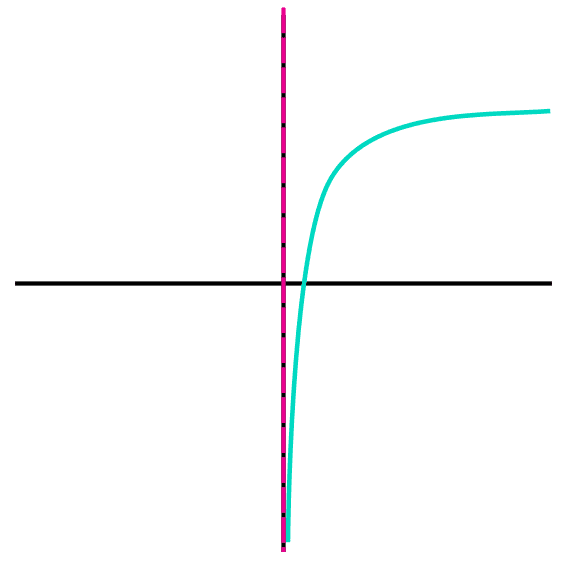
Cómo encontrar el dominio y rango de una Función Logarítmica
En este articulo se enseñarán los pasos principales para encontrar el dominio y rango de una función logarítmica
Dominio y rango de la función logarítmica
Una función logarítmica es aquella que tiene la forma f(x) = logax . Para conocer el dominio y el rango de una función logarítmica se debe comprender ciertas características que un logaritmo debe cumplir.
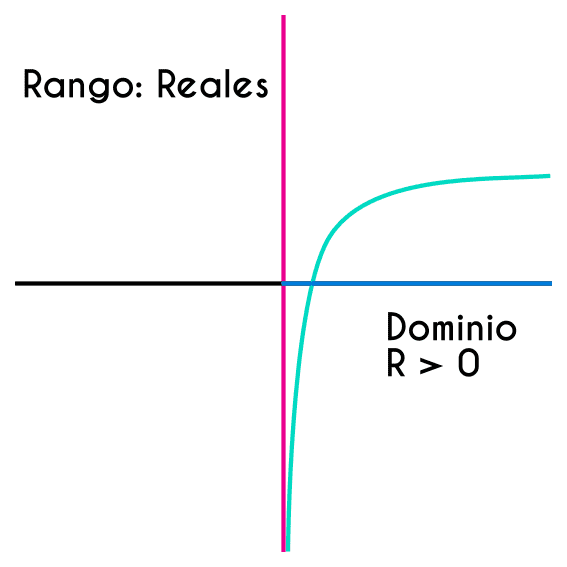
Primero, para conocer cuál es el dominio y rango de una función logarítmica, se debe comprender como es la gráfica de la función logarítmica, y es que la gráfica de este tipo de funciones viene pegada a una asíntota desde menos infinito y esta, en cierto punto comienza a avanzar de forma más lenta hacia el lado derecho.
Dominio de la función logarítmica
Lo primero que se puede ver en la gráfica de la función logarítmica es que el dominio de la función no son todos los reales, sino que el dominio comienza a partir de un punto en “x” donde está ubicada la asíntota, como recordatorio, una asíntota es una linea a la que una función se aproxima lo máximo posible a ella pero jamas la llega a tocar, entonces el dominio de la función logarítmica va desde la asíntota hasta más infinito o hasta menos infinito.
El otro factor a tomar en cuenta es hacia donde se dirige el dominio, si hacia más infinito o hacia menos infinito, y esto va a depender del signo de la variable independiente “x”, si “x” es positiva entonces el dominio de la función irá desde la asíntota hasta más infinito, y si “x” es negativa, entonces el dominio irá desde menos infinito hasta la asíntota.
Ahora bien, para encontrar la ubicación de la asíntota vertical lo que se hace es igualar la ecuación que está dentro del logaritmo a 0, por ejemplo, en la función f(x) = 2log3(3x + 3), lo que se haría es igualar a 0 la ecuación 3x+3 y el resultado dará la coordenada en “x” donde está ubicada la asíntota.
- 3x+3=0
- 3x=-3
- x=
-33
- x = -1
En este caso la asíntota está en “x = -1” y como el signo de la “x” es positivo, el dominio de la función irá desde -1 hasta más infinito sin incluir el -1 porque la asíntota no es parte de la función.
Rango de la función logarítmica
Ahora bien, el rango una función logarítmica son todos los reales, es decir, desde menos infinito hasta más infinito ]-∞, +∞[, esto es así porque el resultado de un logaritmo logab=c es el exponente al que se debe elevar la base “a” para que el resultado sea “b”, es decir: ac=b, y como no hay un limite al que se pueda elevar un número, las posibilidades son infinitas tanto en lo positivo como en lo negativo, porque son todos los reales.
Aunque como se pude ver en la gráfica de la función logarítmica, el crecimiento del rango comienza a ser cada vez más lento a medida que avanzan los valores de “x”, pero a pesar de esto el rango siempre se dirigirá hasta infinito en ambos sentidos.
Ejemplos de dominio y rango de la funcion logarítmica
Ejemplo 1: Encontrar el dominio y rango de f(x) = log4(x - 2)
- Se iguala x-2 a 0
- x-2 = 0
- x = 2
- Entonces la asíntota vertical está en x=2
El dominio de esta funcion va desde 2 hasta más infinito y el rango son los Reales
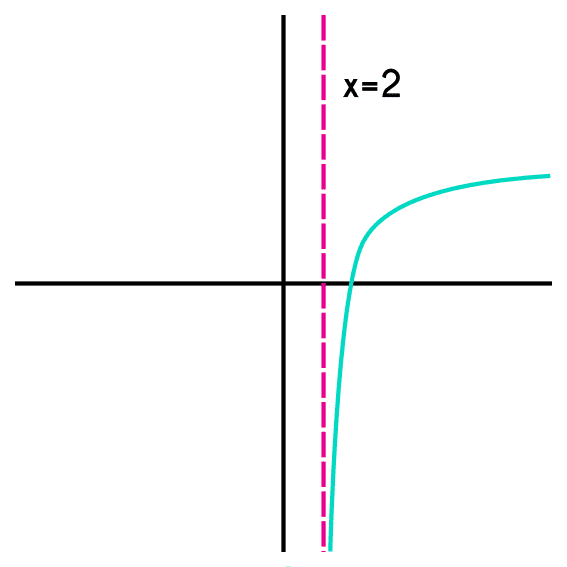
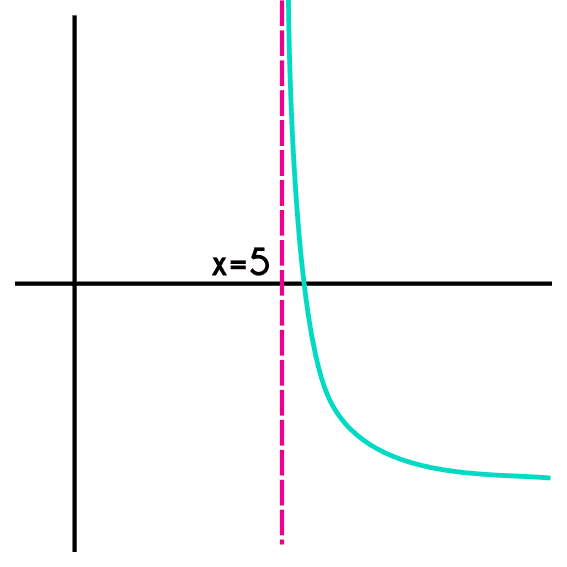
Ejemplo 2: Encontrar el dominio y rango de f(x) = -log2 (2x - 10)
- Se iguala 2x - 10 a 0
- 2x - 10 = 0
- 2x = 10
- x = 10/2
- x = 5
- Entonces la asíntota vertical está en x=5
Aunque el logarítmo en esta función es negativo, esto no cambia la dirección del dominio, por lo tanto el dominio de esta función será desde 5 hasta más infinito, y el rango como siempre son los reales.
Ejemplo 3: determinar el dominio y rango de f(x) = log2(x) + 3
- Se iguala x a 0
- x = 0
- Entonces la asíntota vertical está en x=0
Dominio: ]0 ,+∞[, Rango: ]-∞ ,+∞[