Funciones trigonométricas
En este articulo se desarrollará el tema de las funciones trigonométricas, los tipos de funciones: seno, coseno, tangente, cosecante, secante y cotangente, con sus caracteristicas principales y la forma que tiene cada grafica, a demas de como es el dominio y el rango de cada una de ellas.
Que son las funciones trigonométricas
Las funciones trigonométricas como seno, coseno y tangente y sus inversas cosecante, secante y tangente son parte de las razones trigonométricas las cuales sirven para encontrar las relaciones entre los lados de un triángulo rectángulo y sus ángulos.
Las funciones seno, coseno y tangente son ecuaciones o fórmulas que se ven por primera vez en la resolución de triángulos rectángulos y estas son conocidas como razones trigonométricas, cada una de ellas es una herramienta que se utiliza para encontrar la relación entre los ángulos y lados de un triángulo que tiene un ángulo de 90°.
Cuando se toman estas razones trigonométricas y se forman funciones con ellas hay que tener en cuenta las siguientes condiciones:
No porque una función tenga en la ecuación seno, coseno o tangente significa que es una función trigonométrica, una función es trigonométrica cuando la variable independiente (es decir el dominio que por lo general es el valor de “x”) esta operada por alguna de estas razones, por ejemplo la función f(x) = x sen(90) no es una función trigonométrica porque la “x” no está siendo operada por el seno, sino que está multiplicando un numero constante, porque aunque este esté dado por el seno de 90 este número nunca va cambiar, esta función es lo mismo que estar diciendo f(x) = x * 1, porque “sen(90)” es un numero constante.
En cambio, la función f(x) = 3 tan(x) si es una función trigonométrica porque la variable “x” si está siendo operada por la tangente, por lo cual la función si va a tener la forma de una función trigonométrica.
Diferenciar entre grados y radianes: Una de las cosas en las que hay que tener cuidado es que cuando se evalúa una función trigonométrica, hay que saber en qué unidades de medidas se están tomando los valores de “x”, porque no es lo mismo que “x” tome el valor de 90 radianes, a que "x" tome el valor de 90 grados.
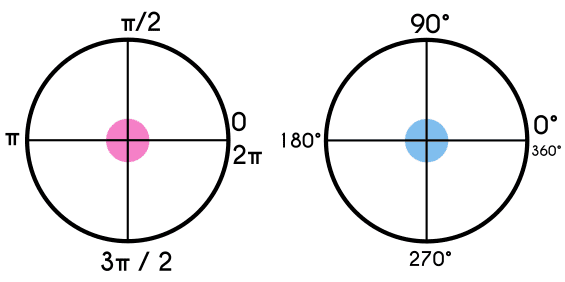
Tanto grados como radianes son medidas de inclinación donde una vuelta completa en grados son 360° mientras que una vuelta completa en radianes son 2Pi radianes (lo equivalente a 6.28318…). El evaluar una función trigonométrica se hace cuando se grafica una de estas, entonces dependiendo de la medida de inclinación que se ocupe también las medidas del grafico tienen que cambiar. Hay que saber configurar la calculadora que se va a usar con la unidad de medida correcta, porque al meter los datos en la calculadora, esta puede que esté configurada en una unidad de medida diferente a la que se esté usando, en temas de funciones trigonométricas la medida que se suele usar con un poco mas de frecuencias son los radianes, pero ambas son igual de válidas.
Ejemplos de funciones trigonométricas
Función seno
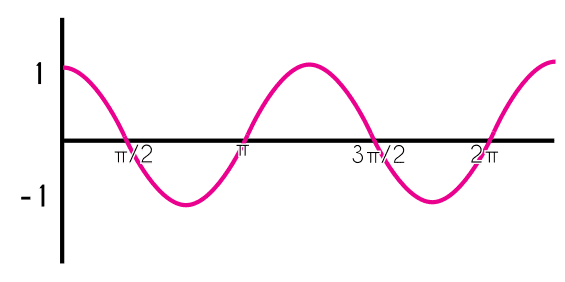
El seno de un triángulo se obtiene dividiendo el cateto opuesto de un triángulo con el valor de la hipotenusa: sen(°)=o/h, la función “general“ del seno ( f(x) = sen(x) ) siempre va a arrojar una valor entre 1 y -1, esto va a cambiar conforme esta valor se vaya multiplicando o sumando con otras constantes como: f(x) = 3sen(x) ó f(x) = sen(x) + 3, por lo que el dominio de esta función nunca van a ser todos los reales, sino que solo una pequeña parte, mientras que el rango de la función sí que son todos los reales.
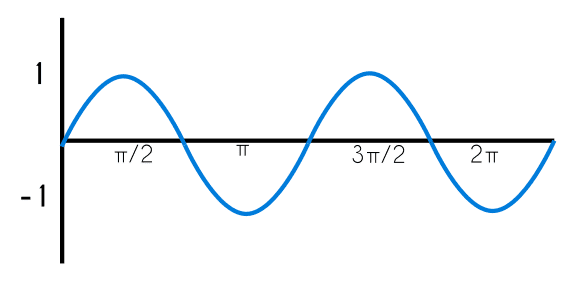
La grafica de la función seno tiene forma de ondas que se repiten indefinidamente, y esta grafica luce de la siguiente manera.
Función coseno
El coseno se puede definir como la división del cateto opuesto entre la hipotenusa: cos=a/h y al igual que la función seno esta siempre arrojará un numero entre 1 y -1, y el rango de esta función serán los reales. La grafica de la función coseno luce exactamente igual que la función seno con la diferencia que estas cortan con el eje “y” en momentos diferentes.
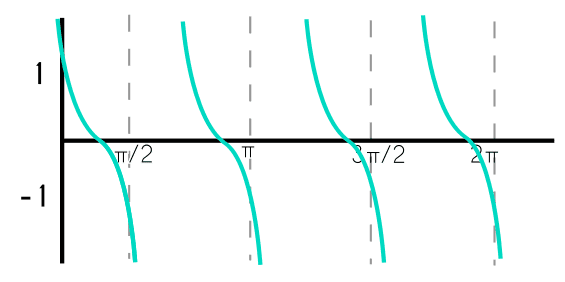
Función tangente
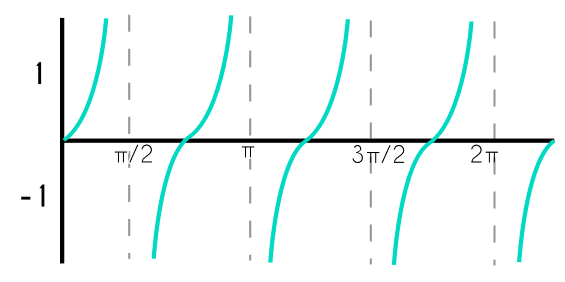
La función tangente es un poco más complicada y confusa que las de seno y coseno, la tangente de un triángulo es la división del cateto opuesto entre el cateto adyacente, a diferencia de las funciones seno y coseno, el dominio de la función tangente no son todos los reales, porque hay algunos valores de “x” que vuelve a la función indeterminada, lo que significa que el dominio se va a acercar a estos puntos de “x” pero jamás los tocará, mientras que el rango de esta función trigonométrica son los números reales, es decir desde menos infinito hasta más infinito.
Función cosecante
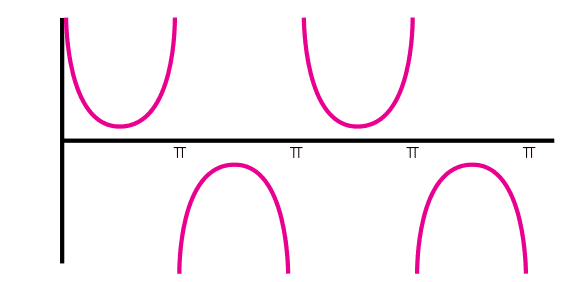
La cosecante se calcula dividiendo la hipotenusa entre el cateto opuesto, en el caso de esta función trigonométrica, ni el dominio ni el rango son los reales, porque hay ciertos números que vuelven a la función indeterminada y el rango no abarca todos los reales. La grafica de esta función son una serie infinita de "parábolas" (entre comillas porque no son exactamente parabolas pero tienen una forma similar) que intercalan entre positivas y negativas.
Función secante
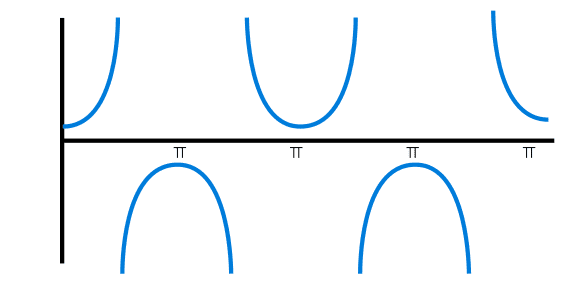
La secante es la división entre la hipotenusa y el cateto adyacente y todo es muy parecido a la función cosecante, las gráficas de estas funciones son las mismas que las de la función cosecante con la diferencia de donde comienzan con respecto a los ejes “x” y “y”
Función cotangente
La cotangente es lo contrario de la tangente, es decir que se obtiene dividiendo el cateto adyacente entre el cateto opuesto, la única diferencia con la función tangente es la dirección de las gráficas