Desviación Típica
En este artículo se expondrá que es la desviación típica, con ejemplos resueltos paso a paso con la fórmula.
Definición de desviación típica
La desviación típica, tambien conocida como desviación estándar es una medida de dispersión, que lo que hace es expresar que tanto varían en promedio los elementos dentro de un conjunto de datos con respecto a su media aritmética, la desviación media no hace diferencia entre números que se desvían hacia arriba de la media o números que se desvían hacia abajo de la media, lo único que importa es el valor promedio que se desvían los datos, sin importar si son números mucho mayores o mucho menores al promedio, por este motivo en la fórmula de la desviación media hace uso de valores absolutos..
La desviación típica es representada con la letra “S” ó también con el símbolo de sigma (σ), la desviación típica también es la raíz cuadrada de la varianza.
La desviación típica es un complemento a las medidas de tendencia central, las cuales buscan un número que esté en el centro de los datos que pueda representar la composición de todo un conjunto de elementos, entonces mientras las medidas de tendencia central representan todo un conjunto en un solo número, la desviación típica por su parte define que tan bien representa la media a todo el conjunto.
El problema con la media aritmética es que esta no siempre da un dato fiable, porque como se explica en el artículo de media, mediana y moda, la media aritmética se ve muy afectada cuando en un conjunto de datos hay números extremadamente altos, o extremadamente bajos, por ejemplo si se tiene el siguiente conjunto de números : {10, 7, 76, 63}, la media aritmética de ese conjunto de números es 39, pero si comparamos este promedio con cada uno de los números, se puede observar que ningún número está cerca del promedio, por lo que la media no es muy fiable a la hora de definir la composición de un grupo de datos.
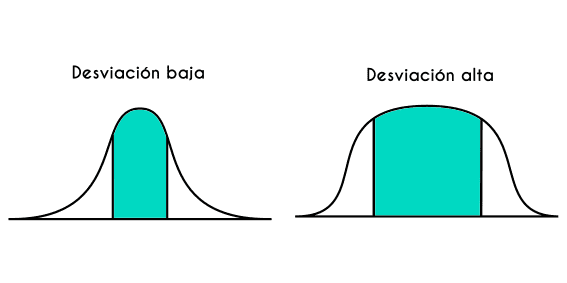
La desviación típica es una solución al problema anterior, pues esta define que tan confiable es la media aritmética, mientras más baja sea la desviación típica de un conjunto de datos, más fiable es el resultado, y viceversa, mientras más alta sea la desviación típica, menos fiable es la media aritmética.
La desviación típica se representa con el siguiente símbolo S y como la desviación típica es el resultado de encontrar la raíz cuadrada de la varianza, la varianza es la desviación típica al cuadrado S2
Fórmula desviación típica
La desviación típica se calcula sacando la raíz cuadrada de la varianza y para la varianza existen 2 formulas diferentes, una para cuando se hace un estudio a una población y otra cuando se hace a una muestra, hay que recordar que una muestra es una parte de la población, por ejemplo, una población puede ser un salón de clase de 45 alumnos, pero una muestra sería un grupo de 10 alumnos de esa clase, por lo que hay que analizar el problema planteado para saber si los datos se recopilan de una población o de una muestra.
- Fórmula de desviación típica con una población
- S2 = √ (
Σ (x - x)2 n)
- Fórmula de desviación típica con una muestra
- S2 = √ (
Σ (x - x)2 n - 1)
Ejemplos desviación típica
Ejemplo 1: Se tomo la edad de los integrantes de un curso de francés, encontrar la desviación típica de las edades.
{18 , 25 , 21 , 22 , 20 , 20 , 19 , 24}
En esta ocasión se estudia la población, por eso se ocupará la fórmula de la varianza en una población, si fuera una muestra, el denominador en lugar de ser "n" seria "n-1"
- Primero se debe encontrar la media (x)
- x =
Σ x n
- x =
18 + 25 + 21 + 22 + 20 + 20 + 19 + 24 8
- x =
169 8
- x = 21.13
- Ahora se encuentra la varianza
- S2 =
Σ (x - x)2 n
- S2 =
(18-21.13)2 + (25-21.13)2 + (21-21.13)2 + (22-21.13)2 + (20-21.13)2 + (20-21.13)2 + (19-21.13)2 + (24-21.13)2 8
- S2 =
(-3.13)2 + (3.87)2 + (-0.13)2 + (0.87)2 + (-1.13)2 + (-1.13)2 + (-2.13)2 + (2.87)2 8
- S2 =
9.80 + 14.97 + 0.017 + 0.76 + 1.28 + 1.28 + 4.53 + 8.24 8
- S2 =
40.87 8
- S2 = 5.11
- Ahora que encontró la varianza se puede encontrar la desviación típica
- S = √ S2
- S = √ 5.11
- S = 2.26
Ejemplo 2: Se quiere hacer un estudio en un hospital de cuantas veces los pacientes que llegan el día de la encuesta se han enfermado de gripe en el transcurso del año, el estudio se realizará solo en base a una muestra de 4 pacientes, calcular la desviación típica de los datos recopilados.
{ 0 , 2 , 1 , 0}
En esta ocasión se estudia una muestra, por lo que se utilizará la fórmula correspondiente a la distribución típica de una muestra
- Como primer paso se encontrará la media (x)
- x =
Σ x n -1
- x =
0 + 2 + 1 + 0 4
- x =
3 4
- x = 0.75
- Luego se encuentra la varianza
- S2 =
Σ (x - x)2 n-1
- S2 =
(0 - 0.75)2 + (1 - 0.75)2 + (2 - 0.75)2 + (0 - 0.75)2 4 -1
- S2 =
(-0.75)2 + (0.25)2 + (1.25)2 + (-0.75)2 3
- S2 =
0.56 + 0.063 + 1.56 + 0.56 3
- S2 =
2.74 3
- S2 = 0.91
- Y conociendo la varianza se puede proceder a calcular la desviación típica
- S = √ S2
- S = √ 0.91
- S = 0.956
Ejemplo 3: Se hace una encuesta a un grupo de trabajo en el que se les pide a algunos de los integrantes evaluar al jefe de su equipo en una escala de 1 a 10 y los resultados fueron los siguientes:
{ 7 , 8 , 7 , 5 , 8}
Conociendo las evaluaciones, calcular la desviacion típica de los resultados
- Como primer paso se debe encontrar la media (x)
- x =
7+8+7+5+8 5
- x =
35 5
- x = 7
- Como segundo paso se encuentra la varianza
- S2 =
Σ (x - x)2 n-1
- S2 =
(7 - 7)2 + (8 - 7)2 + (7 - 7)2 + (5 - 7)2 + (8 - 7)2 5 -1
- S2 =
02 + 12 + 02 + (-2)2 + 12 4
- S2 =
1 + 4 + 1 4
- S2 =
6 4
- S2 = 1.5
- Con la varianza encontrada, se puede encontrar la desviación típica
- S = √ S2
- S = √ 1.5
- S = 1.22