Tablas de frecuencia con ejemplos
En este artículo Se mostrará que son las tablas de frecuencia, para que sirven y como armar una tabla de frecuencia con ejemplos paso a paso
La tablas de frecuencia en estadística son usadas principalmente para poder colocar los datos que se recopilan en un estudio. Las tablas de frecuencia ayudan exponer y analizar los datos de una forma estructurada y de manera que resulte fácil de poder ver los datos, estas tablas presentan todas las variables posibles y la frecuencia que tienen cada una de estas variables, y no solo la frecuencia de cada dato sino que también otros datos que derivan de la frecuencia.
Estas tablas lo que hacen es que clasifican los datos que se recopilan en un estudio determinado de manera que se pueden observar los datos desde varias perspectivas diferentes, como la cantidad de ocasiones que se obtuvo una variable, el porcentaje que representa cada uno de los datos o que porcentajes hay antes y después de un valor.
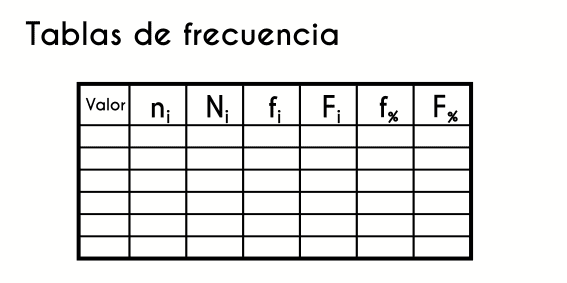
Una tabla de frecuencia está compuesta por lo general por las columnas de la frecuencia absoluta (ni), la frecuencia absoluta acumulada (Ni), frecuencia relativa (fi), frecuencia relativa acumulada (Fi), frecuencia porcentual (n%) y frecuencia porcentual acumulada (F%), aunque estas son las columnas bases de las tablas de frecuencia, hay ocasiones en los que solo se forman en base a los datos que se necesitan en el momento.
| Valor | ni | Ni | fi | Fi | f% | F% |
|---|---|---|---|---|---|---|
| 1 | 4 | 4 | 0.5 | 0.5 | 50% | 50% |
| 2 | 4 | 8 | 0.5 | 1 | 50% | 100% |
| Total | 8 | 1 | 100% |
Estructura de las tablas de frecuencia
Para tener claro como hacer una tabla de frecuencia se utilizará el siguiente ejemplo: Se le pregunto a un grupo de 20 personas la cantidad de vasos de agua que consumen en un día y los resultados fueron los siguientes:
{2,3,5,2,7,8,5,4,6,3,6,3,4,6,2,5,8,9,5,2}
Frecuencia absoluta (ni).
La frecuencia absoluta es la suma de todas las veces que salió una valor, para encontrar la frecuencia absoluta en el ejemplo de los vasos de agua, primero se deben establecer todos los valores que fueron respuesta, sin importar cuantas veces se repite el valor, que en este caso fueron: 2,3,4,5,6,7,8 y 9 y estos valores irán en la primer columna de esta tabla, luego de esto se cuenta la cantidad de veces que cada valor sale, por ejemplo si se observa en el conjunto de datos, el numero dos salió una cantidad de 4 veces, por lo que la frecuencia de 2 será igual a 4, y posteriormente se hace esto con todos los diferentes valores y estos serán la columna dos de la tabla de frecuencia. Al final de la columna se tiene que hacer un total que se obtiene sumando todas las frecuencias.
| Vasos/día | ni |
|---|---|
| 2 | 4 |
| 3 | 3 |
| 4 | 2 |
| 5 | 4 |
| 6 | 3 |
| 7 | 1 |
| 8 | 2 |
| 9 | 1 |
| Total | 20 |
Frecuencia absoluta acumulada (Ni).
Esta frecuencia se obtiene de sumar la frecuencia absoluta de un valor con todas las frecuencias que están antes de ella, por ejemplo, para encontrar la frecuencia acumulada del número 3, se tiene que sumar la frecuencia del valor 3 mas la frecuencia del valor 2, Al realizar estas sumas, la frecuencia acumulada del ultimo numero tiene que coincidir con la suma total de frecuencias.
| Vasos/día | ni | Ni |
|---|---|---|
| 2 | 4 | 4 |
| 3 | 3 | 7 |
| 4 | 2 | 9 |
| 5 | 4 | 13 |
| 6 | 3 | 16 |
| 7 | 1 | 17 |
| 8 | 2 | 19 |
| 9 | 1 | *20 |
| Total | *20 |
Frecuencia relativa (fi).
La frecuencia relativa se obtiene de dividir la frecuencia de una clase por el número total de frecuencias, esto dará un numero entre 0 y 1, y esto representa la proporción de un valor en el número total de resultados.
Una ves calculado la frecuencia relativa de cada clase, se deben sumar para sacar un total, y este debe ser igual a uno, si la suma de todas las frecuencias relativas no es igual a 1 (o por lo menos 0. 99..), es probable que algún calculo este erróneo.
| Vasos/día | ni | Ni | fi |
|---|---|---|---|
| 2 | 4 | 4 | 0.2 |
| 3 | 3 | 7 | 0.15 |
| 4 | 2 | 9 | 0.1 |
| 5 | 4 | 13 | 0.2 |
| 6 | 3 | 16 | 0.15 |
| 7 | 1 | 17 | 0.05 |
| 8 | 2 | 19 | 0.1 |
| 9 | 1 | 20 | 0.05 |
| Total | 20 | 1 |
Frecuencia relativa acumulada (Fi).
Esta se obtiene de sumar todas las frecuencias relativas anteriores, donde el valor de la última frecuencia tiene que ser igual a 1.
| Vasos/día | ni | Ni | fi | Fi |
|---|---|---|---|---|
| 2 | 4 | 4 | 0.2 | 0.2 |
| 3 | 3 | 7 | 0.15 | 0.35 |
| 4 | 2 | 9 | 0.1 | 0.45 |
| 5 | 4 | 13 | 0.2 | 0.65 |
| 6 | 3 | 16 | 0.15 | 0.8 |
| 7 | 1 | 17 | 0.05 | 0.85 |
| 8 | 2 | 19 | 0.1 | 0.95 |
| 9 | 1 | 20 | 0.05 | 1 |
| Total | 20 | 1 |
Frecuencia porcentual (f%).
Esta define la proporción porcentual de una clase con respecto a las demás, es decir, que tanto por ciento de los resultados se encuentran en un valor, el valor de la frecuencia va desde 0% hasta 100% y se obtiene multiplicando la frecuencia relativa por 100, y al sumar todas las frecuencias porcentuales el resultado deberá ser igual a 100.
| Vasos/día | ni | Ni | fi | Fi | f% |
|---|---|---|---|---|---|
| 2 | 4 | 4 | 0.2 | 0.2 | 20% |
| 3 | 3 | 7 | 0.15 | 0.35 | 15% |
| 4 | 2 | 9 | 0.1 | 0.45 | 10% |
| 5 | 4 | 13 | 0.2 | 0.65 | 20% |
| 6 | 3 | 16 | 0.15 | 0.8 | 15% |
| 7 | 1 | 17 | 0.05 | 0.85 | 5% |
| 8 | 2 | 19 | 0.1 | 0.95 | 10% |
| 9 | 1 | 20 | 0.05 | 1 | 5% |
| Total | 20 | 1 | 100% |
Frecuencia porcentual acumulada
Se encuentra sumando la frecuencia porcentual de un valor por todas las anteriores, y la ultima frecuencia tiene que ser igual a 100%.
| Vasos /día | ni | Ni | fi | Fi | f% | F% |
|---|---|---|---|---|---|---|
| 2 | 4 | 4 | 0.2 | 0.2 | 20% | 20% |
| 3 | 3 | 7 | 0.15 | 0.35 | 15% | 35% |
| 4 | 2 | 9 | 0.1 | 0.45 | 10% | 45% |
| 5 | 4 | 13 | 0.2 | 0.65 | 20% | 65% |
| 6 | 3 | 16 | 0.15 | 0.8 | 15% | 80% |
| 7 | 1 | 17 | 0.05 | 0.85 | 5% | 85% |
| 8 | 2 | 19 | 0.1 | 0.95 | 10% | 95% |
| 9 | 1 | 20 | 0.05 | 1 | 5% | 100% |
| Total | 20 | 1 | 100% |
Ejemplos tablas de frecuencia
En estos ejemplos cuando se suman la frecuencia relativa y porcentual, es probable que el resultado no sea exactamente 1 o 100, puede que varíe un número, pero esto es normal debido a que no se ocupan todos los decimales, sino que solo se aproxima a 2 decimales, si se ocuparan todos los decimales entonces el resultado si tuviese que ser 1 para la frecuencia relativa y 100 para la frecuencia porcentual.
Ejemplo 1: Se realizó una encuesta en el que se le preguntaba que animal fue su primera mascota, realizar una tabla de frecuencia con los resultados.
| Mascota | ni |
|---|---|
| Perro | 41 |
| Gato | 23 |
| Tortuga | 13 |
| Total | 77 |
Tabla de frecuencia desarrollada
| Mascota | ni | Ni | fi | Fi | f% | F% |
|---|---|---|---|---|---|---|
| Perro | 41 | 41 | 0.53 | 0.53 | 53% | 53% |
| Gato | 23 | 64 | 0.3 | 0.83 | 30% | 83% |
| Tortuga | 13 | 77 | 0.17 | 1 | 17% | 100% |
| Total | 77 | 1 | 100% |
Con los datos estructurados en esta tabla se puede llegar varias conclusiones, como que el 73% de las personas tuvieron como primer mascota un perro o un gato, asi como este dato, con tablas de frecuencia se pueden sacar conclusiones importantes que ayuden a reforzar una investigación estadística.
Ejemplos 2: Se preguntó a un grupo de deportistas cuál es el deporte que más les gusta practicar, teniendo como respuesta los siguientes deportes: Fútbol, Basquetbol, Voleibol y natación, y los resultados fueron los siguientes
| Deporte | ni |
|---|---|
| futbol | 86 |
| Basquetbol | 57 |
| Voleibol | 30 |
| Natacion | 12 |
| Total | 185 |
Tabla de frecuencia resuelta
| Mascota | ni | Ni | fi | Fi | f% | F% |
|---|---|---|---|---|---|---|
| futbol | 86 | 86 | 0.46 | 0.46 | 46% | 46% |
| basquetbol | 57 | 143 | 0.31 | 0.77 | 31% | 77% |
| voleibol | 30 | 173 | 0.16 | 0.93 | 16% | 93% |
| natacion | 12 | 185 | 0.06 | 1 | 6% | 100% |
| Total | 185 | 1 | 100% |