Media Mediana y Moda

En este artículo Se desglosará cada una de las medidas de tendencia centrales, que son la media, la mediana y la moda cada una con su definición y con ejemplos resueltos

La media, la mediana y la moda son medidas de tendencia central, que tratan de encontrar en una serie de números, un número central desde el cual se extienda la distribución de los demás números, es decir que buscan un número que este en el centro de los demás números, estas tres medidas utilizan diferentes parámetros para poder encontrar ese número. Estas medidas son muy útiles cuando se trata representar una serie de números en un solo valor, aunque la media, mediana y la moda no siempre dan una perspectiva clara de todos los datos.

Cada una de las medidas de tendencia define un número que está en el centro de todos usando criterios diferentes y hay ocasiones en las que se puede tener un resumen más claro de los datos utilizando la moda en lugar de la media o viceversa, por eso se va a definir cada termino con ejemplos para comprender mejor cuando utilizar cada operación.

La media o también llamada media aritmética, se utiliza para encontrar un promedio entre una serie de datos, la media se utiliza únicamente cuando se trata de variables cuantitativas (variables expresadas en números), debido a que no se puede sacar un promedio de variables cualitativas (variables representadas en cualidades). La media aritmetica se representa por una equis con una linea arriba: X

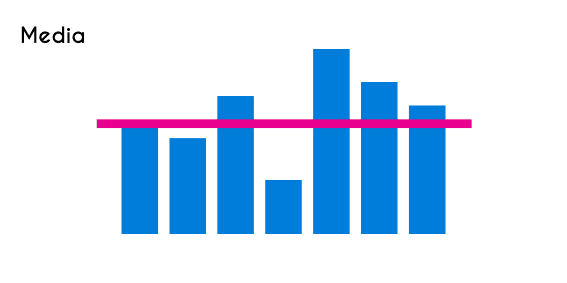
La media resulta útil cuando se quieren comparar dos grupos de datos, por ejemplo si dos personas se interesan por saber quién gasta más dinero a diario y se toman todos los gastos que cada persona hace a lo largo de un mes, al obtener la media de los gastos de cada persona daría la respuesta a esta incógnita.

Algo en lo que media no es muy certera es cuando se quiere saber la composición de un grupo de datos, por ejemplo, si se quiere sacar la media de las notas obtenidas por dos grupos de alumnos, y se tiene que el primer grupo tiene las siguientes notas {7,7,7,7} mientras que en el segundo grupo las notas fueron {10,10,4,4}. Al sacar la media de ambas notas resulta que ambos promedios fueron de 7, este promedio describe a la perfección el primer grupo porque todos son estudiantes “promedios”, pero en el segundo grupo no hay ningún alumno con “notas promedio” sino que hay 2 alumnos excelentes, pero hay dos alumnos regulares.

Lo del ejemplo anterior sucede porque la media aritmética se ve muy influida por los datos extremos, es decir datos que son o muy altos o bajos, y esta es una de las principales dificultades al utilizar la media. La media se calcula sumando todos los elementos que hay en una serie de números y esto se divida entre la cantidad total de elementos.

Ejemplo de como encontrar la media

Encontrar la media: Se realizó un estudio para determinar a que edad las personas preferían comenzar a ir al gimnasio, si se pregunto a 10 personas a que edad comenzaron ellos a asistir al gimnasio ¿Cuál es la media de edad a la que las personas eligieron?

Los resultados fueron: {18, 22, 31, 20, 25, 41, 19, 44, 17, 39}

La mediana se encuentra cuando se ordena una serie de números de mayor a menor o viceversa, y se encuentra cual es el número que esta en medio de la serie. La mediana se encarga de encontrar el valor que esta en el centro de todos los valores, sin importar que tanta diferencia halla entre los valores menores o mayores. Por ejemplo si se tiene los números {1,2,100} la mediana sería el numero 2, sin importar que entre el primer número y la mediana haya 1 de diferencia y entre la mediana y el tercer número haya una diferencia de 98.

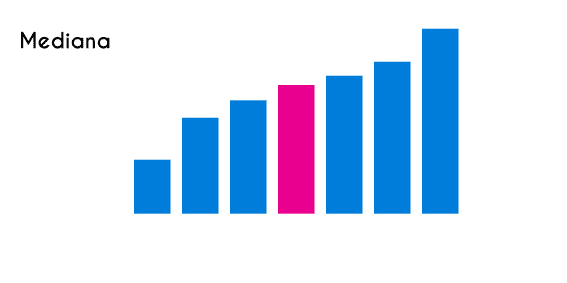
La mediana de una serie que tiene una cantidad de números impar, simplemente se encuentra el numero que esta en el centro, pero cuando la cantidad de números que tiene un grupo de números es par, entonces, este tendrá dos numero que estén en el centro, en estos casos se sacaría un promedio entre ambos números y esta sería la mediana. Al igual que con la media, la mediana solo se puede encontrar en variables cuantitativas.

• Mediana =
  4 + 5 / 2
• Mediana =
  9 / 2
• Mediana = 4.5

La moda es el valor que mas se repite en un grupo de números, el termino moda es quiza el que tiene el nombre más intuitivo, porque tiene mucho que ver con la palabra moda que se ocupa normalmente, cuando algo esta “a la moda”, ya sea que se hable de un estilo de ropa, un telefono celular, una aplicación, es porque la mayor parte de la gente los esta usando, algo parecido sucede con la moda en matemáticas, pues es el valor que más es utilizado en una serie.

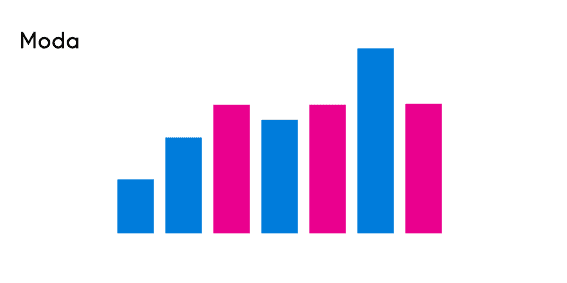
A diferencia de la media y la mediana, la moda si puede ser utilizada con variables cualitativas, esto porque para encontrar la moda no es necesario hacer ningún proceso con números, simplemente se cuenta la frecuencia con la que aparece un elemento. Cuando en una serie son dos los valores que se repiten más entonces se considera que es una serie bimodal, y en caso de que hayan 3 o mas modas, entonces se denominaría multimodal.

Ejemplo de como encontrar la moda

Por ejemplo: En un grupo de trabajo de 11 personas se pregunta cuál es el animal domestico que mas les gusta y los resultados fueron los siguientes

{perro, gato, perro, loro, perro, gato, conejo, gato, gato, perro, conejo}

Como se explica anteriormente, la moda es la única medida de tendencia que puede ser utilizada con variables cuantitativas, y en esta ocasión fueron dos los animales más elegidos, que fueron el perro y el gato, entonces aquí se puede apreciar una distribución bimodal.

Artículos relacionados