Cuartiles

En este artículo Se dará la definición de cuartiles, fórmula para encontrarlos y Ejemplos resueltos paso a paso

Definición de cuartiles

Los cuartiles son una herramienta en estadística la cual permite dividir una serie o un conjunto de números en 4 partes iguales, de esta manera se pueden clasificar los números en 25%, en 50%, y en 75%. Al igual que sucede con la desviación típica y las medidas de tendencia central, los cuartiles ayudan a tener una mejor perspectiva de la dispersión de los datos, pero en este caso no en torno a un promedio sino que basado en porcentajes.

Cuartil 1

Cuartil 2

Cuartil 3

Cuartil 4

Los cuartiles no son números que se calculan con alguna formula sino que son elementos propios de un conjunto de datos los cuales indican que hasta es numero (cualquier cuartil) hay un porcentaje especifico de datos. Aunque los cuartiles no son valores que se definen a través de una fórmula, si que existe una fórmula que define la posición exacta donde está ubicado un determinado cuartil porque cuando la serie de números es muy grande es complicado ubicarlos sin tener la posición exacta.

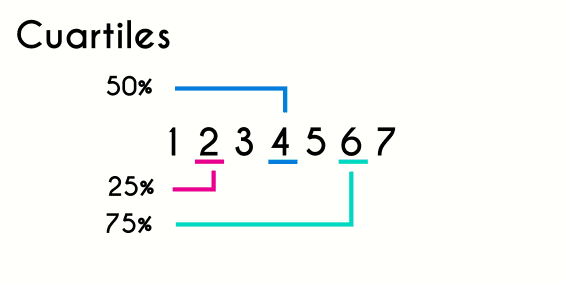
Los cuartiles se encuentran cuando se tiene una serie ordenada, es decir, que para encontrar los cuartiles en la siguiente serie: {9,3,7,5,1,2,4,8} esta tendría que ser ordenada primero, ya sea de menor a menor: {1,2,3,4,5,7,8,9} o de mayor a menor: {9,8,7,5,4,3,2,1}. El tipo de orden que se le dé a un conjunto de datos va a depender del propósito del estudio y del análisis que se le quiera dar a los datos recopilados, pero cualquiera de los ordenes que se le aplique a una serie de números es valido para encontrar los cuartiles.

Incluso hay ocasiones donde para analizar un problema desde diferentes perspectivas se deben encontrar los cuartiles en una misma serie 2 veces, una ordenada de mayor a menor y otra de menor a mayor, pero en estos casos una vez encontrados los cuartiles en cualquiera de los ordenes, lo único que se debe hacer es invertir el orden del primer y tercer cuartil porque la posición donde se ubican será la misma, pero el primer cuartil (25%) pasa a ser el tercer cuartil (75%) y el segundo cuartil se queda en a misma posición porque esta en el centro siempre.

Los cuartiles son 3 números que dividen los datos de un conjunto de datos en 4 partes, donde hasta el primer cuartil hay un 25% de los datos, hasta el segundo cuartil hay un 50% de los datos y hasta el tercer cuartil hay un 75% de los datos.

El segundo cuartil siempre va a coincidir con la mediana, esto sucede porque el segundo cuartil, al igual que la mediana, es el número que está en medio de una serie de números ordenada, esto pasa siempre y cuándo la cantidad total de números sea impar, porque en caso que la cantidad de números sea par entonces habrán 2 números centrales, en este caso lo que se hace comúnmente, al igual que con la mediana, es encontrar un promedio entre los 2 números.

Otra propiedad de los cuartiles es que el primer cuartil estará entre el primer número y el segundo cuartil y el tercer cuartil estará entre el segundo cuartil y el ultimo número de la serie.

Problema de cuartiles

Para tener una mejor perspectiva del uso correcto de los cuartiles en la practica se realizará el siguiente ejemplo: Se tomo la altura (en centimetros) de 7 miembros de una empresa, encontrar los cuartiles de las estaturas tomadas.

Para encontrar los cuartiles, primero se ordenan los datos de menor a mayor

Luego se encuentra el número que está en el centro y este será el cuartil número dos, que a la vez es la mediana.

Luego de esto se encuentra el número que está entre el segundo cuartil y el primer número y ese será el primer cuartil

Y por último se encuentra el número que este entre el último dato y el segundo cuartil y este será el tercer cuartil

Los cuartiles ayudan a poder dar conclusiones de los datos en porcentajes, en este caso el primer cuartil es 168, por lo que se pude decir que el 25% de los datos son igual o menor a 168, el segundo cuartil es 173, entonces el 50% de los datos es igual o menor a 173, y por último, el tercer cuartil es 177, y como el tercer cuartil siempre es el 75% de los datos, se puede concluir que el 75% de los datos son iguales o menores que 177.

Hay ocasiones donde es muy fácil encontrar los cuartiles de una serie de números, tanto que se pueden encontrar unicamente observando los números, pero este proceso se complica bastante cuando la cantidad de números que hay en un conjunto crece y encontrar los cuartiles se vuelve mas difícil, para estos casos lo más practico es utilizar la siguiente fórmula la cual da como resultado la posición en la que está cada uno de los cuartiles, ojo, recalcar que está fórmula no da el valor de los cuartiles sino que da la posición, por ejemplo en el siguiente conjunto de números {4,5,7,12,44,45,90,100,130} el segundo cuartil está en la posición 5, que sería el número 45.

En esta fórmula la variable Q se refiere a los cuartiles, la letra k es el número de cuartil que se quiere encontrar (1, 2 o 3) y “n” es la cantidad total de datos que hay en una serie de números y en este caso como se habla de cuartiles se divide entre cuatro.

Cuando la posición de un cuartil da un número decimal, existen diferentes maneras de tomar este resultado, pero en estos ejemplos se hará de la siguiente manera: si la posicion de un cuartil da un número que esta exactamente en medio de dos números (por ejemplo 3.5 está en medio de 3 y 4), entonces se hará una promedio entre los dos números, pero cuando la posición del cuartil es un número decimal que no está en medio de dos números (por ejemplo 5.25 o 6.75) entonces se aproximara el valor de la posicion de los cuartiles.

Artículos relacionados