Cómo graficar una Función Radical con Ejemplos
En este articulo se mostrará como encontrar la grafica de una función con una raíz cuadrada
Lo primero que hay que entender para graficar cualquier función radical es que el dominio de la función radical no son los reales, esto quiere decir que la función inicia en cierto punto de “x” y avanza ya sea hacia el lado izquierdo o hacia el lado derecho en el plano cartesiano, por lo que no siempre es efectivo evaluar la función en valores de “x” cercanos al origen, porque es probable que los valores que se seleccionen no sean siquiera parte del dominio de la función radical.
Pero entonces, ¿Que datos hay que tomar para graficar una función radical?, lo primero que hay que entender es que el valor de “x” determinará hacia donde avanzará la función, si “x” es positiva avanzará hacia la derecha y si de lo contrario es negativa entonces la función avanzará hacia la izquierda, esto es importante de saberlo porque así se pueden escoger los valores de “x” dependiendo de hacia donde se dirija la gráfica de la función.
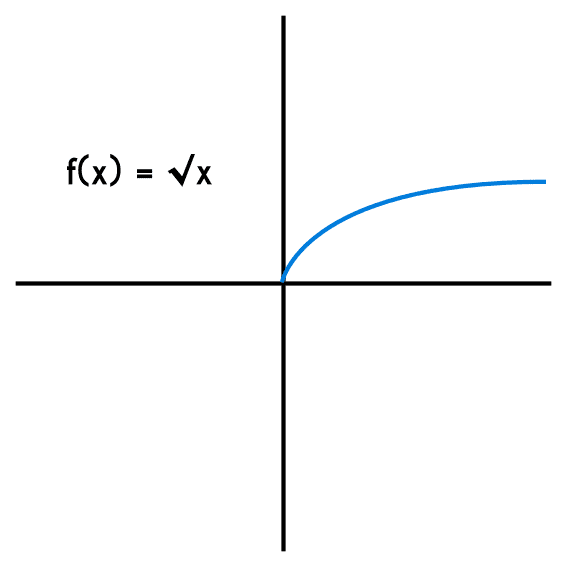
Una vez conociendo la dirección hacia donde crece el radical lo siguiente que hay que hacer es encontrar el punto en “x” donde comienza la función radical, para ello se debe de igualar a 0 la ecuación que esté dentro de la raíz cuadrada y posteriormente se despeja la variable “x” y el resultado será el punto donde la función inicia.
Habiendo realizado los 2 pasos anteriores lo que se hace es tomar los valores de “x” cercanos al punto que se encontró dependiendo de la dirección de la función radical. Para comprender mejor los pasos explicados, se desarrollará el siguiente ejemplo: Graficar la siguiente función radical f(x) = √(x – 5).
Esta función se dirige hacia la derecha (hasta más infinito) porque la raíz es positiva, entonces lo que se hará será encontrar el punto donde inicia la función.
- Se iguala a 0 la ecuación dentro del radical
- x - 5 = 0
- x = 5
Ahora sabiendo que la función comienza en x=5 y se dirige hacia infinito se tomarán datos próximos mayores que x=5, por ejemplo = 5, 6, 7, 8 y 9, y se evaluará la función en estos números en una tabla de valores.
| x | f(x) = √(x – 5). | y |
|---|---|---|
| 5 | f(5) = √(5 – 5). | 0 |
| 6 | f(6) = √(6 – 5). | 1 |
| 7 | f(7) = √(7 - 5). | 1.41 |
| 8 | f(8) = √(8 - 5). | 1.73 |
| 9 | f(9) = √(9 - 5). | 2 |
Cuándo ya se tienen las coordenadas que pertenecen a la función f(x) = √(x – 5), simplemente se dibuja el plano cartesiano, se ubican los puntos y por ultimo se traza una linea que pase por cada coordenada.
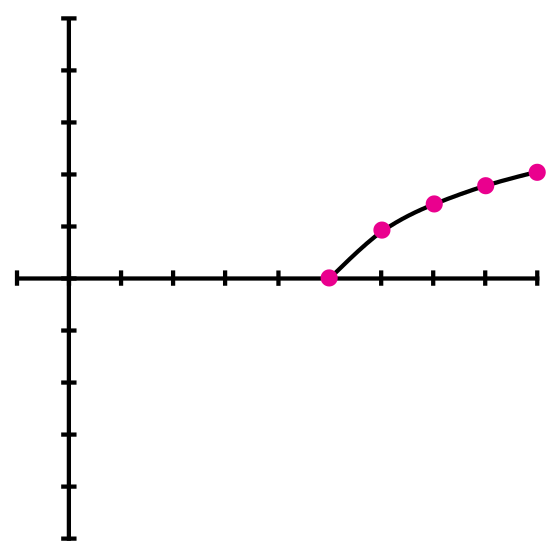
Ejemplos de grafica de un radical
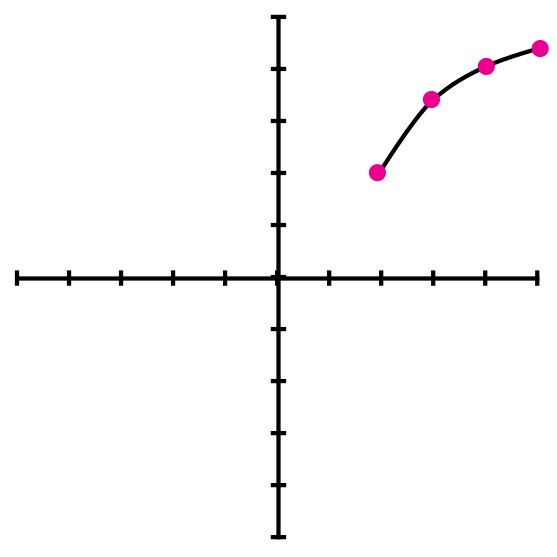
Ejemplo 1: Graficar la función f(x) = √(2x – 4) +2
- Se iguala a 0 la ecuación dentro del radical
- 2x - 4 = 0
- 2x = 4
- x = 4/2
- x = 2
Esta función va a crecer hacia mas infinito, por lo tanto se tomarán valores mayores a 2
| x | f(x) = √(2x – 4) + 2 | y |
|---|---|---|
| 2 | f(2) = √(2(2) – 4) + 2 | 2 |
| 3 | f(3) = √(2(3) – 4) + 2 | 3.41 |
| 4 | f(4) = √(2(4) – 4) + 2 | 4 |
| 5 | f(5) = √(2(5) – 4) + 2 | 4.45 |
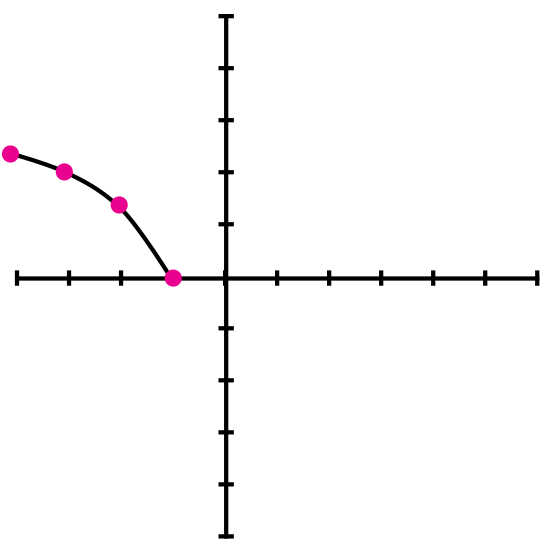
Ejemplo 2: Graficar la función f(x) = √(-2x - 2)
- Se iguala a 0 la ecuación dentro del radical
- -2x -2 = 0
- -2x = 2
- x = 2/-2
- x = -1
Cómo la "x" es negativa esta crece hasta menos infinito, y se tomarán valores menores a -1, porque el dominio de la función comienza en x=-1.
| x | f(x) = √(-2x – 2) | y |
|---|---|---|
| -1 | f(-1) = √(-2(-1) – 2) | 0 |
| -2 | f(-2) = √(-2(-2) – 2) | 1.41 |
| -3 | f(-2) = √(-2(-3) – 2) | 2 |
| -4 | f(-4) = √(-2(-4) – 2) | 2.45 |