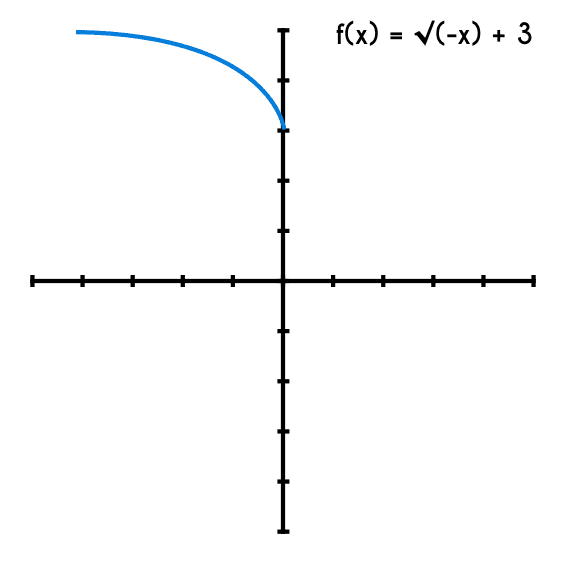Dominio y Rango de una función radical
En este articulo se mostrará como definir el dominio y rango de una función radical
Para encontrar el dominio y rango de una función radical (una función con la variable independiente dentro de una raíz) primero se debe comprender como funciona una función radical y que condiciona el dominio y rango de la función raíz cuadrada.
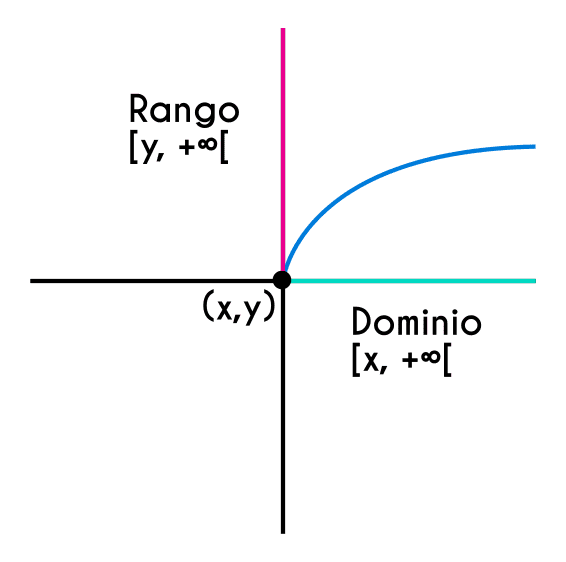
Primero que nada hay que conocer la gráfica de la función, y es que si se observa la gráfica esta comienza desde cierto punto de (x,y) y esta va a ir creciendo cada vez más hacia alguno de los lados, esto quiere decir que tanto el domino como el rango iniciarán en cierto punto y comenzarán a dirigirse hacia más infinito o hacia menos infinito tanto en “x” como en “y”, por lo tanto ni el dominio ni el rango de una función radical son los reales.
Entonces lo que se tiene que hacer es encontrar este punto (x,y) donde comienza, y para ello hay que comprender un factor importante en una raíz cuadrada, y es que, no existe una raíz cuadrada de un número negativo o inferior a 0, por lo tanto este punto va a estar cuando la variable o la ecuación que esta dentro de la raíz cuadrada sea cero.
Teniendo en cuenta lo anterior, cuando se tiene una función donde “x” esté sola ( √x) entonces se sabe que va a ser desde x=0 hacia infinito, pero cuando la “x” está siendo multiplicada o sumada por otros números entonces lo que se hace es tomar la ecuación que está dentro de la raíz e igualarla a 0, y luego se despeja la variable “x” y el resultado será el punto en “x” en el que el dominio de la función inicia.
Y para encontrar la coordenada “y” del inicio de la función radical simplemente se evalúa la función la coordenada “x” que se encontró anteriormente.
Ahora que ya se sabe como encontrar el punto donde la función radical comienza lo siguiente será conocer hacia adonde se dirige su dominio y rango. El dominio de una función radical crecerá hacia mas infinito si el signo de la raíz cuadrada es positiva, de lo contrario, si la variable es negativa entonces el dominio llegará hasta menos infinito, importante que esto es el signo de “la raíz” y no de la variable, es decir √x irá hasta infinito y -√x; irá hacia menos infinito.
En cuanto al rango este dependerá del signo de la variable independiente “x”, si “x” es positiva entonces el rango irá hacia infinito, en cambio si “x” es negativo el rango se dirigirá hasta menos infinito.
Ejemplos de dominio y rango funcion radical
Ejemplo 1: Encontrar el dominio y rango de una función f(x) = √(x + 2) + 3
- Primero se despeja la ecuacion que está en el radical para encontrar donde inicia la función
- x + 2 = 0
- x = -2
- Se evalua la funcion en "x = -2"
- f(x) = √(x + 2) + 3
- f(-2) = √(-2 + 2) + 3
- f(-2) = √(0) + 3
- f(-2) = 0 + 3
- f(-2) = 3
- por lo tanto la función inicia en (-2,3)
Ahora que se conoce el punto de inicio de la función se debe analizar hacia adonde se dirige la función: El dominio va desde -2 hasta más infinito (porque el signo de la raíz es positivo) y el rango va desde 3 hasta más infinito (porque la variable "x" es positiva)
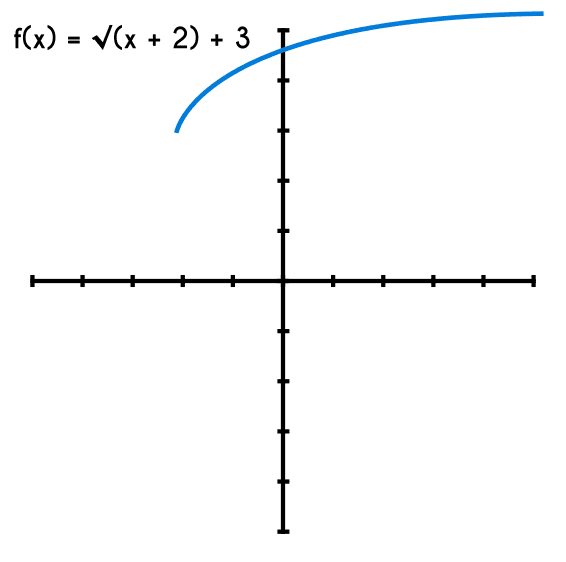
Ejemplo 2: Encontrar el dominio y rango de una función f(x) = -√(3x + 12)
- Se iguala la ecuación a 0
- 3x + 12 = 0
- 3x = -12
- x = -12/3
- x = -4
- Se evalua la funcion en "x = -4"
- f(x) = -√(3x + 12)
- f(-4) = -√(3(-4) + 12)
- f(-4) = -√(-12 + 12)
- f(-4) = -√(0)
- f(-4) = 0
- por lo tanto la función inicia en (-4,0)
El dominio de esta función va desde -4 hasta más infinito, y el rango desde 0 hasta menos infinito (porque el signo del radical es negativo)
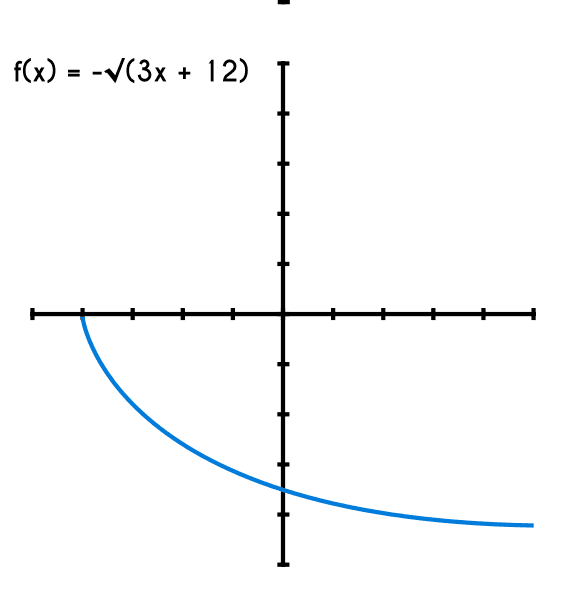
Ejemplo 3: Encontrar el dominio y rango de la siguiente función f(x) = √(-x) + 3
- Cómo la "x" está sola entonces el inicio es en x=0
- x = 0
- Se evalua la función en "x = 0"
- f(x) = √(x) + 3
- f(0) = √(0) + 3
- f(0) =0 + 3
- f(0) =3
- por lo tanto la función inicia en (0,3)
el dominio va desde 0 hasta mas menos infinito (porque "x" es negativa), y el rango desde 3 hasta más infinito