Regla del complemento
En este artículo se explicará que es la regla del complemento, con las fórmulas y ejemplos.
¿Qué es la regla del complemento?
La regla del complemento es uno de los numerosos métodos que hay en estadística que sirve para determinar la probabilidad de un suceso en particular. Primeramente a este método se le llama regla del “complemento” haciendo referencia a cuando un espacio muestral se representa en un diagrama de Venn, solo para recordar, estos diagramas se basan en círculos donde cada círculo representa un suceso aleatorio y el conjunto de todos los círculos es el espacio muestral.
Otro aspecto que hay que recordar es que a un círculo (que en caso de probabilidades representa un suceso en concreto), se le pone un nombre cualquiera, por ejemplo un suceso llamado “A”, y a todo lo que no pertenesca a el suceso A se le llama Complemento de A. (usualmente el complemento de un suceso se representa con la misma letra del suceso pero con una raya arriba de la letra A).
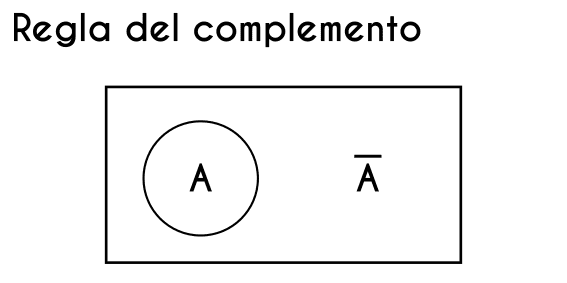
Ahora teniendo claro a que se refiere con complemento en este método, se entiende que cuando se usa la regla del complemento en probabilidad se usa para encontrar todo lo que no tenga que ver con un suceso en concreto, en otros métodos de probabilidad como la regla de la suma, probabilidad empírica, probabilidad clásica, etc, (enlaces a los artículos al final de la página) siempre se busca la probabilidad de un suceso pero en la regla del complemento se busca lo contrario, es decir, la probabilidad de que el suceso no ocurra.
La regla del complemento se aplica en problemas donde encontrar la probabilidad de un suceso o conjunto de sucesos es complicado, porque la cantidad de sucesos a encontrar es mayor a la cantidad de sucesos que no se encuentran, y es mas fácil encontrar la probabilidad los sucesos que no nos interesan y basados en la probabilidad de estos, se encuentra la probabilidad de los sucesos que nos interesa, basándose en que la probabilidad de todos los sucesos de un espacio muestral deben sumar exactamente 1.
Ejemplo para entender la aplicación de la regla del complemento
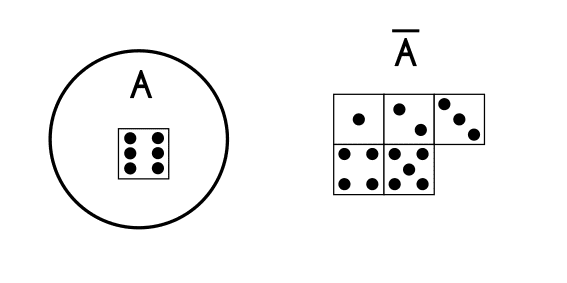
Para comprender mejor en que situaciones es útil la regla del complemento se pondrá un ejemplo sencillo: como ya se sabe cuando se tira un dado hay 6 posibles sucesos, uno por cada lado del dado y estos componen al conjunto del espacio muestral y todos los lados tienen la misma probabilidad de salir, entonces si se quiere saber cual es la probabilidad de que al lanzar un dado este caiga en un número inferior a 6, ¿Cómo se haría con la regla del complemento?.
Con otros métodos de probabilidad lo que se haría es encontrar la probabilidad de las caras 1, 2, 3 ,4 y 5, porque es lo que se busca, pero en la regla del complemento se hace lo contrario y es que es mas fácil encontrar la probabilidad de 1 suceso y luego restarle eso a 1 (que es la suma de todas las probabilidades), que encontrar la probabilidad de 5 sucesos.
En el ejemplo anterior quizás no se note mucho el beneficio de usar la regla del complemento, pero este era solo como ejemplo para ver como funcionaba la ley del complemento, pero cuando se tienen sucesos donde no todos estos tienen las mismas probabilidades, es entonces que se nota la diferencia entre usar un método tradicional de probabilidad y usar la regla del complemento.
Fórmula de la regla del complemento
- Fórmula
- p( a ) = 1 - p(a)
Ejemplos de la regla del complemento
Ejemplo 1: Cuál es la probabilidad de que al lanzar un dado, este salga cualquier numero diferente a 1 y 6
- Primero se encuentra p(a)
- Siendo p(a), la probabilidad de que salga el lado 1 o 6
- p(a) = 2 / 6
- p(a) = 0.3333
- Ahora se encuentra p( a )
- p( a ) = 1 - 0.3333
- p( a ) = 0.6666
- p( a ) = 0.6667
- p( a ) = 0.6667 * 100%
- p( a ) = 66.67%
Ejemplo 2: Un joven va a comprar un modelo de telefono el cual viene en 10 colores diferentes, pero a él no le gustan dos colores en los que este teléfono viene, si al comprar el telefono, le tocara un color al azar, ¿Cuál es la probabilidad de que no le salga uno de los colores que a el joven no le gusta?
- Primero se encuentra p(c)
- Siendo p(c) la probabilidad que toque un color no deseado
- p(c) = 2 / 10
- p(c) = 0.2
- Ahora se encuentra p( c )
- p( c ) = 1 - 0.2
- p( c ) = 0.8
- p( c ) = 0.8 * 100%
- p( c ) = 80%
Ejemplo 3: En una empresa están haciendo que sus empleados hagan horas extras un día de la siguiente semana entre lunes y sábado, pero una de las empleadas de esta empresa tiene el cumpleaños de su hijo el viernes después del trabajo, si las horas extras se reparten al azar, cual es la probabilidad que a esta empleada le toque un día que no sea el viernes
- Primero se encuentra p(h)
- p(h) = horas extras el dia viernes
- p(h) = 1 / 6
- p(h) = 0.1667
- Ahora se encuentra p( h )
- p( h ) = 1 - 0.1667
- p( h ) = 0.8333
- p( h ) = 0.8333 * 100%
- p( h ) = 83.33%
Ejemplo 4: En una tienda de helados hay 4 sabores diferentes a escoger, según estadísticas de la heladería el sabor preferido de los clientes es el chocolate, por lo que se esta agotando y no quieren que las personas pidan helados de chocolate porque de esa manera se agotaría más rápido, entonces, ¿Qué tan probable es que el siguiente cliente pida un helado de un sabor diferente al chocolate?
- Primero se encuentra p(s)
- p(s) = sabor de chocolate
- p(s) = 1 / 4
- p(s) = 0.25
- Ahora se encuentra p( s )
- p( s ) = 1 - 0.25
- p( s ) = 0.75
- p( s ) = 0.75 * 100%
- p( s ) = 75%
Ejemplo 5: Un maestro está poniendo a algunos de sus estudiantes a leer una lección para toda la clase, si el profesor va a poner a leer a 7 de sus 40 alumnos, pero ninguno de estos quiere leer en voz alta, ¿Qué probabilidad tienen los estudiantes que no les toque leer?
- Primero se encuentra p(L)
- p(L) = sabor de chocolate
- p(L) = 7 / 40
- p(L) = 0.175
- Ahora se encuentra p( L )
- p( L ) = 1 - 0.175
- p( L ) = 0.825
- p( L ) = 0.825 * 100%
- p( L ) = 82.5%