Probabilidad total
En este artículo Se definirá que es la probabilidad total, como se usa con su fórmula y una serie de varios ejercicios con su respectiva resolución
¿Qué es la probabilidad total?
La probabilidad total es un método que se usa en estadística que sirve para encontrar la probabilidad de un suceso del cual no se conoce los casos favorables ni nada en general a este suceso, sino que se da como un complemento de otros sucesos, por lo tanto, lo que se tiene acerca del suceso que se quiere encontrar es que la probabilidad está repartida en 2 o más partes. Por esto a este método se le llama “probabilidad total”, porque con el se puede encontrar la probabilidad general de un suceso del cual solo se tienen partes divididas.
Para entender mejor las situaciones en las que se emplea la probabilidad total, se propondrá el siguiente enunciado, (La resolución a este problema se hará en la parte de ejercicios, más abajo en este artículo): Hay una discusión en un grupo el cual quiere poner un color a su equipo de trabajo y se barajan 2 colores en específico, el 60% de los integrantes del grupo piensan que el color debe ser el negro, mientras que el otro 40% quiere que el color que los identifique sea el verde, si se sabe un 40% de los que quieren el color negro y un 30% de los que piden que el color sea verde son hombres, ¿Cuál es la probabilidad de que al seleccionar un integrante del grupo aleatoriamente este sea hombre?
Como se puede observar en el problema anterior, el dato general del porcentaje total de integrantes del grupo que sean hombres no se da, pero lo que si se da es que porcentaje de cada preferencia de color es hombre, es decir que un 40% de un 60% y un 30% de un 40% son hombres. Entonces para encontrar la probabilidad general de que alguien elegido al azar sea hombre se usa la probabilidad total (resolución a este problema más abajo).
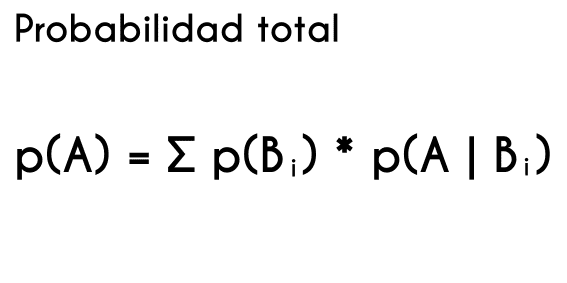
Una herramienta que es bastante útil para poder resolver problemas de probabilidad total es el diagrama de árbol, este se ocupa primeramente para esquematizar el problema que se plantea y con eso se puede identificar más fácilmente los datos que se tienen que multiplicar y sumar para llegar a la respuesta.
Fórmula de la probabilidad total
La formula de la probabilidad total ocupa el principio de la multiplicación, que lo que hace es multiplicar la probabilidad de dos o más sucesos que ocurran a la vez, por ejemplo en el enunciado del ejemplo anterior, si se quiere encontrar la probabilidad que una de las personas que proponen el color negro sea hombre, se multiplicaría el porcentaje de las personas que les gusta el color negro, por el porcentaje de hombres que les gusta el color negro, también se haría lo propio con las personas que prefieren el color verde, es decir el porcentaje de personas que les gusta el verde por los hombres a los que les gusta el verde, y al tener estos dos resultados, estos se suman y asi se llegaría a la probabilidad total de que alguien seleccionado sea hombre.
En el diagrama de árbol se multiplican todos los resultados que hay en una misma rama, y al final se suma la respuesta de todas las ramas.
- Fórmula de la probabilidad total
- p(a) = Σ p(bi) * p(a | bi)
En el caso de esta fórmula, se deben ocupar probabilidades entre 0 y 1, no en porcentajes, por lo que si hay el problema da probabilidades en porcentajes estos se deberían dividir entre 100 para poder introducirlos en la fórmula
Ejercicios de probabilidad total
Ejercicio 1: Se resolverá el ejercicio planteado anteriormente: Se discute cual debe de ser el color que represente a un equipo de trabajo, el 60% proponen el color negro, de los cuales el 40% son hombres, y el otro 40% proponen el color verde, de los cuales el 30% son hombres, entonces ¿Cuál es la probabilidad que al seleccionar un miembro del equipo este sea de género masculino?
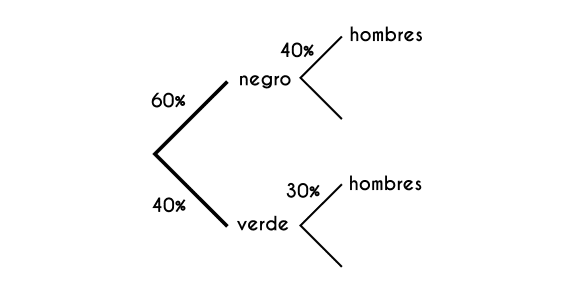
h = hombre n = color negro v = color verde
- Primero se resolvera cada rama por separado y por último se sumaran los resultados, para que sea menos confusa la formula
- p(n) * p(h | n)
- 0.6 * 0.4
- 0.24
- p(v) * p(h | v)
- 0.4 * 0.3
- 0.12
- Ahora se suman todos los resultado (al final se multiplica por 100 para obtener el resultado en porcentaje)
- 0.24 + 0.12
- 0.36 * 100%
- 36%
Ejercicio 2: En un concesionario de automóviles hay coches 3 tipos de coches: sedanes (40%), camionetas (50%) y deportivos (10%), si el 10% de cada tipo de coche son de color rojo, ¿Cuál es la probabilidad que al seleccionar uno aleatoriamente este sea de dicho color?
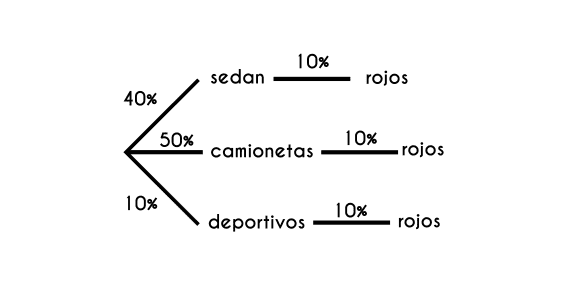
s = sedán c = camioneta d = deportivo
- p(s) * p(r | s)
- 0.4 * 0.1
- 0.04
- p(c) * p(r | c)
- 0.5 * 0.1
- 0.05
- p(d) * p(r | d)
- 0.1 * 0.1
- 0.01
- Ahora se suman todos los resultados
- 0.04 + 0.05 + 0.01
- 0.1 * 100%
- 10%
Ejercicio 3: A una iglesia asisten varias personas, de las cuales el 65% son mujeres y el 35% son hombres, si el 60% de las mujeres y el 30% de los hombres son casados, ¿Qué tan probable es que al preguntarle a cualquier persona sin importar el género si está casado/a esta responda que sí?
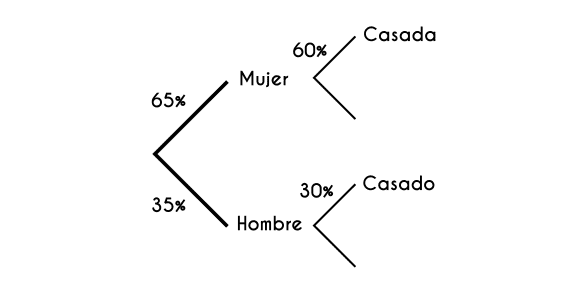
h = hombre m = mujer c = casado/a
- p(m) * p(c | m)
- 0.65 * 0.6
- 0.39
- p(h) * p(c | h)
- 0.35 * 0.3
- 0.105
- Ahora se suman todos los resultados
- 0.39 + 0.105
- 0.495 * 100%
- 49.5%
Ejercicio 4: Se hizo una encuesta ente adultos y adolescentes donde se les preguntaba cuál era su género de música favorito, el 70% de los encuestados eran adolescentes y el otro 30% estaba compuesto por adultos, si el 20% de los adolescentes y el 80% de los adultos respondieron que su genero favorito era el rock, ¿Cuál es la probabilidad que al seleccionar a uno de los encuestados, su género preferido sea el rock?
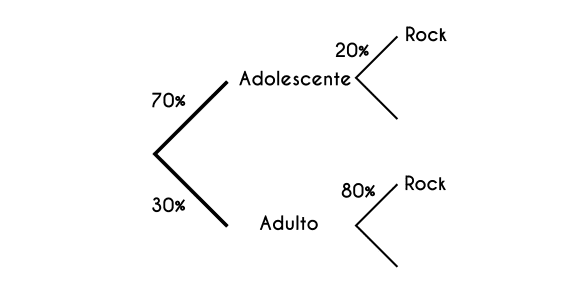
a = adolecentes A = adultos r = rock
- p(a) * p(r | a)
- 0.7 * 0.2
- 0.14
- p(A) * p(r | A)
- 0.3 * 0.8
- 0.24
- Ahora se suman todos los resultados
- 0.14 + 0.24
- 0.38 * 100%
- 38%