Regla de la suma
En este artículo Se estudiará el tema de la regla de la suma en probabilidad, con su fórmula y ejemplos de como aplicarla en probabilidades
Definicion de la regla de la suma en probabilidad
La regla de la suma es un método que se usa para poder encontrar una probabilidad compuesta, se considera una probabilidad compuesta cuando se unen 2 sucesos para formar otro suceso, conociendo esto, la regla de la suma se usa cuando se quiere conocer cual es la probabilidad que sucedan 2 o más eventos, ya sea al mismo tiempo o solamente uno de los 2.
Para poder pasar a resolver ejercicios de la regla de la suma primero hay que aprender la notación con la que vienen estos problemas, que al inicio puede parecer un poco confuso, pero una vez se logra comprender, es muy sencillo.
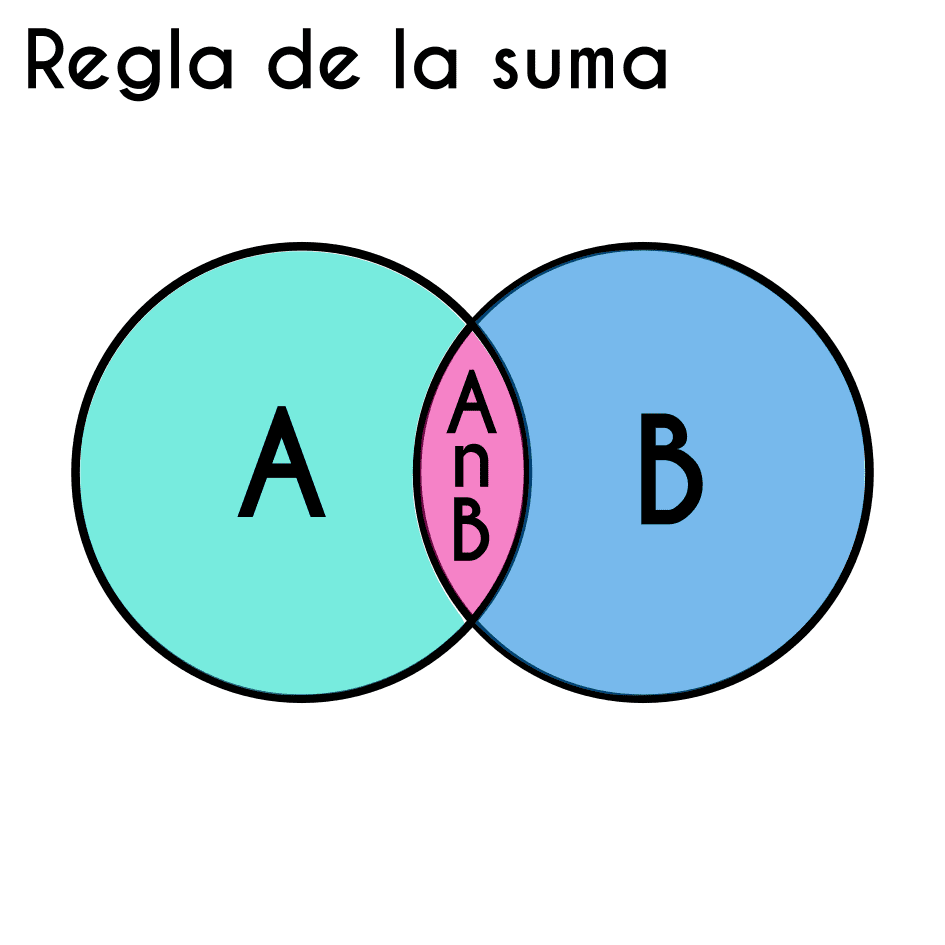
Conceptos para resolver ejemplos de la regla de la suma
Recordatorio de como se escriben las probabilidades
Las probabilidades siempre se escriben de la siguiente manera p(a), donde “p” es la probabilidad y “a” es el suceso que puede suceder, por ejemplo, cuando se tira una moneda al aire existen dos sucesos posible, que caiga cara o que caiga cruz, pues para diferenciarlos se podría a llamar al suceso donde cae cara p(a) y al suceso donde cae cruz p(b), aunque si se quiere poner mas preciso este experimento, existe también un tercer suceso, y es cuando la moneda cae parada, que la probabilidad que esto pase es muy pequeña, se ha demostrado en estudios que la probabilidad que esto pase es de 1 en 6000 en condiciones perfectas, pero eso es otro tema.
Terminos utiles en la regla de la suma
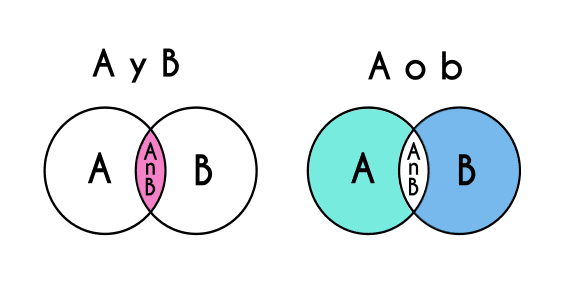
Habiendo recordado lo anterior ahora se puede pasar a la notación de la regla de la suma. Primero hay que saber utilizar tanto el ”y” como el “o”, y es que se utiliza “y” cuando se refiere a que suceden ambos sucesos al mismo tiempo, por ejemplo “Hace calor y está lloviendo”, en esta oración se indica que están pasando ambos sucesos al mismo tiempo, es decir que hace calor mientras que llueve, en cambio en la oración “Hace frio o hace calor” tiene un significado diferente, porque quiere decir que o esta haciendo frio o está haciendo calor, pero no ambas.
En la regla de la suma se utiliza el mismo lenguaje pero escrito de diferente manera: p (a n b) significa la probabilidad de a y b , es decir, la probabilidad que suceda tanto "a" como "b", y p(a u b) se refiere a la probabilidad de a ó b, es decir que ocurre un suceso o ocurre el otro, pero no ambos a la vez.
A p(a n b) se le puede decir "a intersección b", y a p(a u b) también se le conoce como "a union b"
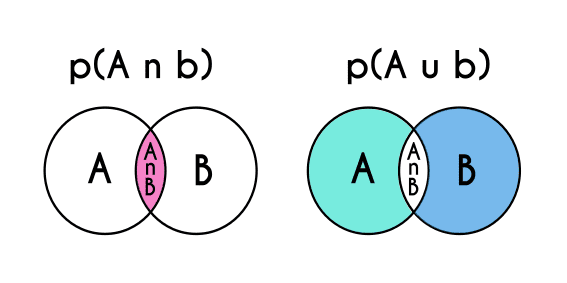
Fórmula de la regla de la suma
Para poder usar la regla de la suma de manera correcta antes se tienen que encontrar las probabilidades individuales de los sucesos, y cuando ya se tengan las probabilidades es que se usa la siguiente fórmula para por poder encontrar la probabilidad que se busca.
- Fórmula de la regla de la suma
- p(aub) = p(a) + p(b) - p(anb)
Ejemplos de la regla de la suma
Ejemplo 1: En una sala hay 20 personas, donde se sabe la mitad de las personas son mayores de 30 años, si se sabe que hay 7 mexicanos de los cuales 5 son mayores de 30 años, ¿Cuál es la probabilidad de que al seleccionar una persona al azar salga alguien que sea mayor de 30 años o que sea de México?
p(m) = mexicano, p(M) = mayor, p(m n M) = mexicano y mayor de 30
- Primero se calculará las probabilidades por separado
- p(m) = 7 / 20
- 0.35
- p(M) = 10 / 20
- 0.5
- p(m n M) = 5 / 20
- 0.25
- Ahora se encuentra p(m u ma)
- p(m u M) = 0.35 + 0.5 - 0.25
- p(m u M) = 0.6 * 100%
- p(m u M) = 60%
Ejemplo 2: En una tienda se venden silla de color verde y de color rojo, si hay 16 sillas (8 rojas y 8 verdes) a escoger pero hay 10 de madera y 6 de plástico y se sabe que de las 6 de plástico hay 5 que son verdes ¿Qué tan probable es que si se escoge una silla cualquiera, esta sea verde o de plástico?
p(v) = verde, p(p) = plastico, p(v n p) = verde y de plastico
- Primero se calculará las probabilidades por separado
- p(v) = 8 / 16
- 0.5
- p(p) = 6 / 16
- 0.375
- p(v n p) = 5 / 16
- 0.3125
- Ahora se encuentra p(v u p)
- p(v u p) = 0.5 + 0.375 - 0.3125
- p(v u p) = 0.5625 * 100%
- p(v u p) = 56.25%
Ejemplo 3: Una maquina dispensadora de refrescos tiene en su interior 50 bebidas, y cada vez que se utiliza esta dispensa una al azar, si se conoce que en su interior tiene 25 bebidas de color negro, y también se sabe que hay 40 que están heladas y de estas solo 20 son bebidas de color negro, ¿Cuál es la probabilidad que al sacar una bebida esta esté helada o sea negra?
p(N) = bebida negra, p(h) = helada, p(N n h) = bebida negra y helada
- Primero se calculará las probabilidades por separado
- p(N) = 25 / 50
- 0.5
- p(h) = 40 / 50
- 0.8
- p(N n h) = 20 / 50
- 0.4
- Ahora se encuentra p(N u h)
- p(N u h) = 0.5 + 0.8 - 0.4
- p(N u h) = 0.9 *100%
- p(N u h) = 90%