Probabilidad condicional
En este artículo Se va a desarrollar el tema de la probabilidad condicional, para que sirve, en que situaciones hacer uso de ella, con su fórmula y ejemplos.
Probabilidad condicional
La probabilidad condicional se da cuando hay una posibilidad que un suceso ocurra habiendo pasado otro suceso anteriormente, es decir que la mayoría de los ejemplos se plantearan de la siguiente manera: “Cual es la probabilidad que ocurra el suceso A dado que ha ocurrido el suceso B” o “Cual es la probabilidad que suceda el evento A sí ya ocurrió el evento B”.
Para entender mejor como es que funciona la probabilidad condicional se ocupará un diagrama de Venn, pues como ya se dijo, esta probabilidad es útil cuando hay 2 sucesos, suponiendo que estos se llaman A y B, y lo que se quiere encontrar es cual es la probabilidad de que ocurra un suceso cuando ya ocurrió el otro, ojo, no significa que se va a encontrar A intersección B (AnB), sino que se va a encontrar la probabilidad del suceso A tomando como punto de referencia todo lo que tenga que ver con el suceso B incluyendo aquí (AnB).
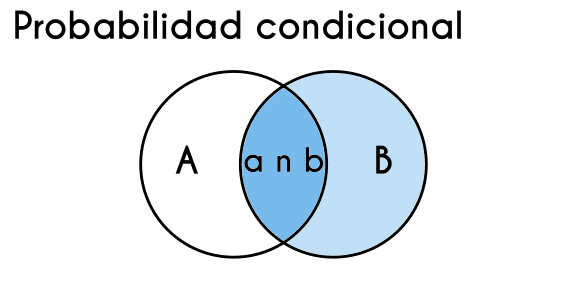
Por ejemplo, si tanto el suceso A como el suceso B tienen un 50% de probabilidades de ocurrir y la probabilidad de que ambos ocurran al mismo tiempo es del 25%, lo que se puede encontrar con la probabilidad condicional es la probabilidad que el suceso A ocurra habiendo ocurrido el evento B, ojo, esto no es el 25%, porque este 25% representa a cuando pasen los 2 sucesos al mismo tiempo sin importar cuál haya ocurrido antes, y lo que se busca es que pase primero el B y a partir de ahí encontrar la probabilidad que pase el suceso A.
Si lo anterior no ha quedado muy claro, se hará con el siguiente ejemplo: Una creencia muy común en la mayoría de jóvenes y adultos es que los adolescentes que son muy buenos en el estudio son por lo general malos para los deportes y los que son buenos para los deportes no son buenos estudiantes, entonces en una escuela se hizo un estudio sobre esto, y se llegaron a los siguientes resultados: el 30% de los alumnos son buenos estudiantes mientras que otro 20% son buenos en el deporte, también se llego al resultado que el 5% de los alumnos de esta escuela son buenos en ambas cosas. En un diagrama de ven se podría representar de la siguiente manera. E = buenos estudiantes, D = buenos deportistas
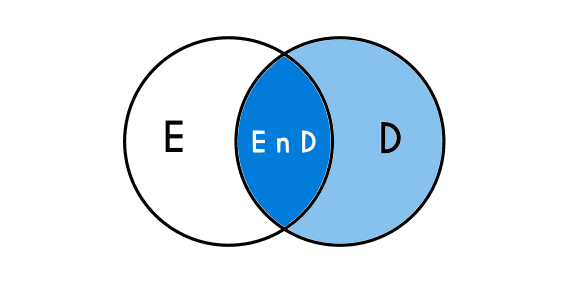
Entonces si con los resultados anteriores se plantea la pregunta: ¿Cuál es la probabilidad que un alumno que es bueno en los deportes este también sea muy buen estudiante?, entonces la probabilidad es condicional, ojo, la respuesta no es el 5%, porque el 5% es el porcentaje de los alumnos en general que son buenos en ambas cosas, pero lo que se pregunta es la probabilidad que en el grupo de los que son buenos deportistas, también haya alguien que sea buen estudiante (Este ejercicio se resolverá más abajo).
Fórmula de la probabilidad condicional
En esta fórmula no importa si se ocupan las probabilidades en porcentajes (de 1 a 100) o entre 0 y 1, al final el resultado será el mismo, esto porque las proporciones de las cantidades se mantienen, pero para obtener el resultado en porcentaje, esté se tiene que multiplicar por 100%.
- Fórmula de probabilidad condicional
- p(a | b) = p(a n b)p(b)
- Fórmula de probabilidad condicional (resultado en porcentaje)
- p(a | b) = p(a n b)p(b)* 100%
Ejemplos de la probabilidad condicional
Ejemplos 1: Se resolverá el ejercicio propuesto anteriormente: si el 30% de los alumnos son buenos estudiantes mientras que un 20% son buenos deportistas y solamente un 5% son buenos en ambas cosas, encontrar la probabilidad de que al seleccionar un alumno que sea un buen deportista, este también sea bueno en el estudio.
e = buenos estudiantes d = buenos deportistas
- p(e | d) = p(e n d)p(d)
- p(e | d) = 5%20%
- p(e | d) = 0.25 * 100%
- p(e | d) = 25%
Ejemplos 2: En un acuario hay peces de varios colores y tamaños, si se sabe que el 30% de los peces son rojos y que el 42% de los peces son grandes, y aparte se sabe que el 20% de los peces son grandes y rojos, ¿Cuál es la probabilidad que al sacar un pez grande, este también sea rojo?
r = peces rojos g = peces grandes
- p(r | g) = p(r n g)p(g)
- p(r | g) = 20%42%
- p(r | g) = 0.4762
- p(r | g) = 47.62%
Ejemplos 3: Se sabe que el 20% de las familias de un país poseen al menos un vehículo, y también se conoce que el 70% de las familias tienen al menos 2 hijos, y aparte se sabe que un 19% de las familias tienen coche y más de 2 hijos, entonces ¿Cuál es la probabilidad de que al seleccionar una familia que tiene un coche, esta tenga al menos 2 hijos?
2h = mas de dos hijos v = posee vehículo
- p(2h | v) = p(2h n v)p(v)
- p(2h | v) = 19%20%
- p(2h | v) = 0.95
- p(2h | v) = 95%
Ejemplos 4: En una perrera el 50% de los perros son peludos y el 10% de los perros son blancos, si se conoce que el 2% de los perros son peludos y blanco, ¿Cuál es la probabilidad que al seleccionar un perro peludo, este sea blanco?
b = perro blanco p = perro peludo
- p(b | p) = p(b n p)p(p)
- p(b | p) = 2%50%
- p(b | p) = 0.04
- p(b | p) = 4%
Ejemplos 5: En una empresa hay un 3% de los trabajadores que tienen ojos de color verde y un 20% que tiene el cabello rizado, si se conoce que el 1% tienen los ojos de color verde y tienen cabello rizado, ¿Cuál es la probabilidad que si se selecciona una persona de cabello rizado esta tenga los ojos de color verde?
v = ojos verdes r = cabello rizado
- p(v | r) = p(v n r)p(r)
- p(v | r) = 1%20%
- p(v | r) = 0.05
- p(v | r) = 5%