Regla de la multiplicación
En este artículo Se dará la definición de la regla de la multiplicación en probabilidad, como aplicarla, con las fórmulas y ejemplos.
¿Qué es la regla de la multiplicación en probabilidad?
La regla de la multiplicación es un proceso que se ocupa cuando se quiere calcular la probabilidad de que 2 o más sucesos pasen al mismo tiempo, usando un diagrama de Venn para representar a las probabilidades se puede observar de manera grafica lo que se encuentra usando la regla de la multiplicación.
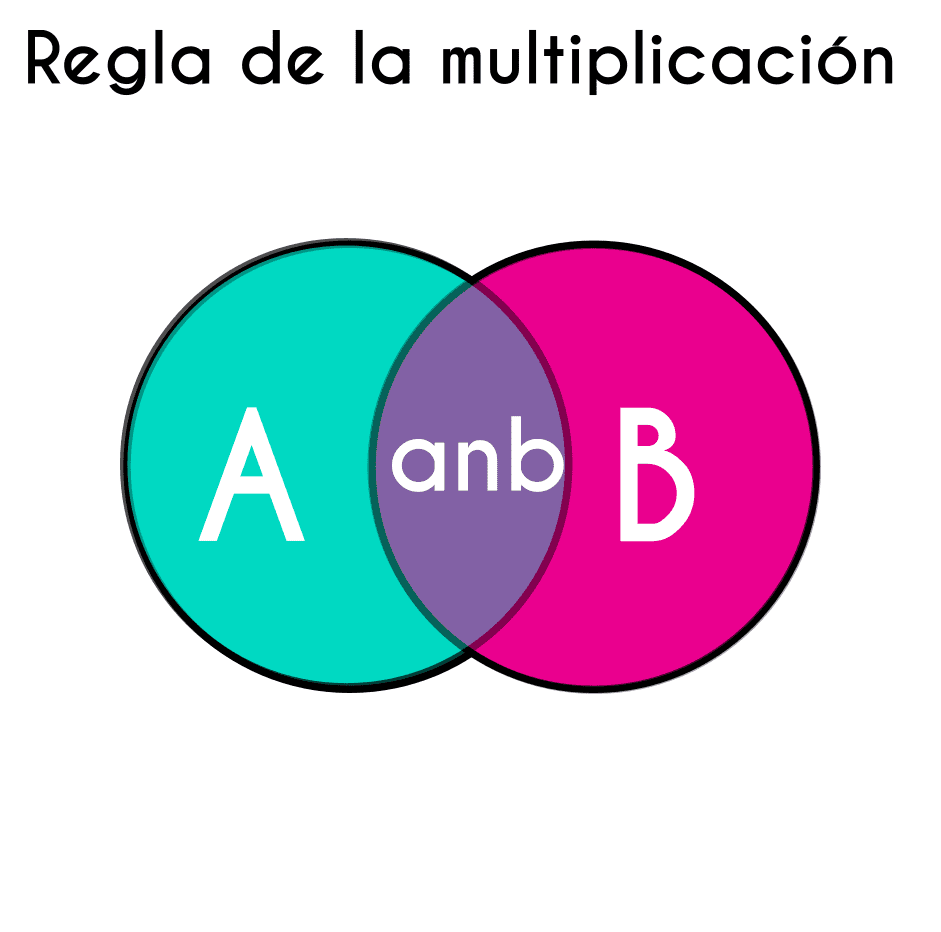
Como se puede observar en la imagen anterior lo que se busca con la regla de la multiplicación es la intersección entre 2 o más sucesos de un mismo espacio muestral, escrito matemáticamente sería “p(a n b)” que quiere decir “la probabilidad de ‘a’ intersección ‘b’ ”.
Variantes en la regla de la multiplicación
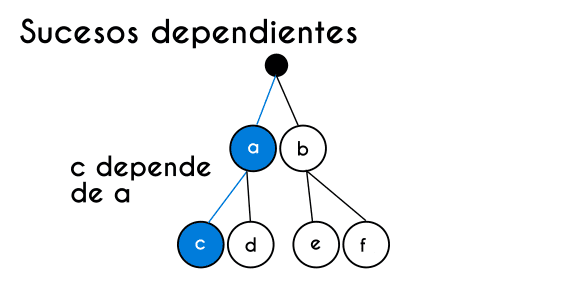
En la regla de la multiplicación existen 2 escenarios diferentes, una es cuando los sucesos son independientes, que es cuando la ocurrencia de un suceso no afecta a la probabilidad del otro, y la otra cuando los sucesos son dependientes, es decir que la ocurrencia de un suceso afecta la probabilidad del otro, y para cada uno de estos casos se usa una fórmula diferente, por ende la manera en la que se resuelven los problemas cambia un poco, por esto hay que tener claro cuando se trata de sucesos dependientes y cuando se trata de sucesos independientes.
Ejemplo de sucesos independientes: Se van a sacar dos bolas de un bote el cual en su interior tiene un total de 31 bolas, de las cuales 5 bolas son amarillas, 9 rojas y 17 marrones, si se saca una primero y otra después ¿Cuál es la probabilidad de que la primera sea marrón y la segunda amarilla? En este caso se esta hablando de un suceso dependiente, porque al sacar la primera bola la probabilidad sería 17/31, pero a la hora de sacar la segunda ya no hay 31 bolas disponibles, sino que hay solo 30, porque se acaba de sacar una, entonces la ocurrencia del primer suceso afecta al segundo suceso.
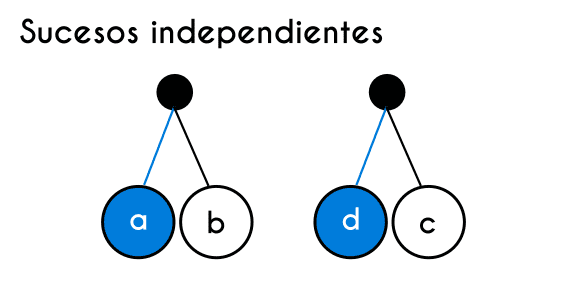
Ejemplo de sucesos dependientes: Si en una heladería sirven dos tipos de helados, una es en un cono y otra es en un vaso, y aparte hay 4 sabores a elegir (vainilla, pistacho, chocolate y fresa), ¿Cuál es la probabilidad de que al llegar una persona al azar ordene un helado en vaso y este sea de chocolate? En este ejemplo el primer suceso (tipo de helado) no afecta en nada el segundo suceso (sabor del helado), es por esto por lo que se denominan sucesos independientes.
Fórmulas de la regla de la multiplicación
Por lo general en problemas de la regla de la multiplicación no se es claro si el ejemplo presenta sucesos dependientes o independientes, esto normalmente se define por comprensión lectora y análisis del problema, por esto se recomienda leer detenidamente el enunciado del problema para saber con que tipo de sucesos se está trabajando (dependiente o independiente) para escoger la fórmula correcta.
Hay 2 formulas diferentes en la regla de la suma, una por cada tipo de sucesos
En la fórmula donde el primer suceso tiene efecto sobre el segundo está la variable p(b|a), esto quiere decir “la probabilidad de ‘b’ habiendo ocurrido ‘a’ ”.
- Fórmula cuando la probabilidad del primer suceso no afecta al segundo
- p(a n b) = p(a) * p(b)
- Fórmula cuando la probabilidad del primer suceso tiene efecto sobre el segundo
- p(a n b) = p(a) * p(b | a)
Ejemplos de la regla de la multiplicación
Ejemplo 1: ¿Cuál es la probabilidad que al lanzar una moneda tres veces, esta caiga las tres veces cara?
- En este ejercicio son sucesos independientes por lo que se ocupara la fórmula de probabilidades independientes
- p(a n b n c) = p(a) * p(b) * p(c)
- a, b y c es la probabilidad de salir cara
- p(a n b n c) = 1/2 * 1/2 * 1/2
- p(a n b n c) = 1/8
- p(a n b n c) = 0.125 * 100%
- p(a n b n c) = 12.5%
Ejemplo 2: Si en un grupo de 10 personas se va a repartir refrescos de 10 sabores diferentes, y se sabe que hay uno de fresa y uno de piña ¿Cual es la probabilidad que el primero en ser repartido sea de piña y el segundo de fresa?
- En este ejercicio son sucesos dependientes, por eso se ocupará la siguiente fórmula
- p(f n p) = p(a) * p(b | a)
- p(f n p) = 1/10 * 1/9
- p(f n p) = 0.011 * 100%
- p(f n p) = 1.1%
Ejemplo 3: En una tienda se venden osos de peluche, en existencia hay 30 de estos peluches, si entre estos hay 15 marrones y 15 blancos, y en la tienda tienen estadisticas que indican que 4 de cada diez de los clientes terminan comprando estos peluches ¿Cuál es la probabilidad que el siguiente cliente compre un oso de color blanco?
c = comprar un oso, b = oso blanco
- Fórmula de sucesos independientes
- p(c n b) = p(c) * p(b)
- p(c n b) = 4/10 * 1/2
- p(c n b) = 0.2 * 100%
- p(c n b) = 20%
Ejercicio 4: Cual es la probabilidad que al tirar un dado 2 veces salga el mismo número.
a = que salga un cualquier lado, b = que salga el mismo lado que en "a"
- Fórmula de sucesos independientes
- p(a n b) = p(a) * p(b)
- p(a n b) = 1/6 * 1/6
- p(a n b) = 0.027 * 100%
- p(a n b) = 2.7%