Permutación

En este artículo Se definirá que es la permutación y para que sirve con ejemplos.

¿Qué es la permutación?

La permutación es un método matemático comúnmente usado en estadística donde se define de que tantas formas diferentes se pueden ordenar los elementos de un conjunto en un subconjunto de una menor cantidad de elementos, por ejemplo, si se tiene un conjunto de 20 elementos, la permutación permitiría encontrar la cantidad de formas diferentes que se pueden seleccionar cierta cantidad de elementos del conjunto principal.

La repetición de elementos no es algo que esté permitido en la permutación, esto quiere decir que un elemento no se puede seleccionar 2 o más veces en un permutación, algo que si se puede en la combinación.

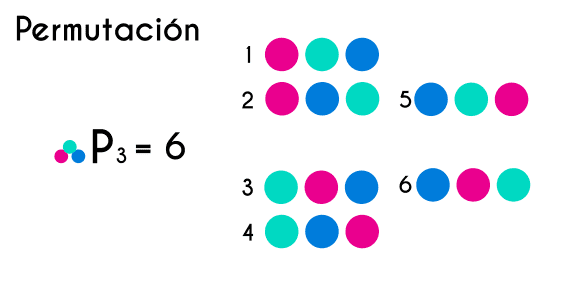
Descripcion

Algo que si es debe tener en cuenta en la permutación es que el orden en el que los elementos del conjunto son posicionados si hacen la diferencia, esto quiere decir que si, por ejemplo se tienen que ordenar 3 elementos, en la permutación no solo se toma en cuenta que estos 3 elementos coincidan en un mismo escenario sino que también se toma en cuenta el orden en el que están colocados cada uno de los elementos, donde por cada orden se toma como una permutación diferente.

Como se explica en la definición de la permutación, esta sirve para definir de cuantas formas posibles se pueden clasificar u ordenar un conjunto de elementos en un subconjunto más pequeño formado por los elementos del conjunto general, cuando se habla de un subconjunto se refiere a que se va a extraer cierta cantidad de elementos del conjunto para formar otro conjunto, si esto aun no queda del todo claro se recomienda pasar a la parte de los ejemplos.

Ejemplo práctico de permutación

Para entender un poco mejor que es la permutación y para qué sirve se realizará el siguiente ejemplo: Se tiene un valde con 4 bolas que están nombradas con las letras a, b, c y d, y se sacan dos, no las dos a la vez sino que una primero y otra después ¿De cuantas maneras se pueden sacar las 2 bolas?

A continuación una tabla con todos los casos posibles.

N° Bola 1 Bola 2
1 A B
2 A C
3 A D
4 B A
5 B C
6 B D
7 C A
8 C B
9 C D
10 D A
11 D B
12 D C

Nótese como las permutaciones número 1 y número 4 están compuestas por las mismas bolas pero estas se toman como permutaciones diferentes, esto se hace así porque el orden de los elementos, que en este caso es el orden en el que se sacaron las bolas importa en la permutación y no solamente la combinación de bolas.

En total hay 12 posibles maneras de sacar 2 bolas de un conjunto de 4 bolas, visto con este ejemplo quizás parezca sencillo de calcular usando una tabla como la anterior o con un diagrama de árbol, pero cuando la cantidad de elementos de un conjunto es mayor entonces se complica demasiado, y es por eso que se usa la fórmulas de la permutación que permite resolver estos problemas de forma más fácil, este ejemplo se resolvió de esta forma con el fin que se comprenda de forma practica que es la permutación.

Fórmula de la permutación

La fórmula de la permutación utiliza factoriales, que como recordatorio, el factorial de un numero es el numero multiplicado por todos los números enteros bajo de él, por ejemplo el factorial de 4 es: 4! = 4x3x2x1 = 24, donde también se sabe que la factorial de 0 es igual a 1.

La permutación se escribe de la forma nPr, donde n es el número total elementos que se tiene un conjunto, mientras que r es el subconjunto en el que se pueden ordenar todos los elementos, donde r no puede ser mayor que n.

  • Fórmula
  • nPr =
    n!/(n-r)!

Ejemplos de permutación

Ejemplo 1: Hay una competición entre 5 equipos de futbol, si se premiara con una medalla al 1er, 2do y tercer puesto, ¿de cuantas maneras pueden ser formado el podio?

n = 5 r = 3 5P3 = ?

  • nPr =
    n!/(n-r)!
  • 5P3 =
    5!/(5-3)!
  • 5P3 =
    5!/2!
  • 5P3 =
    5*4*3*2*1/2*1
  • 5P3 =
    120/2
  • 5P3 = 60

Ejemplo 2: Si se selecciona al azar a los ganadores del primer premio y del segundo premio de una rifa que se realizó en un grupo de 10 personas ¿Cuántas combinaciones de personas pueden ganar los premios?

n = 10 r = 2 10P2 = ?

  • nPr =
    n!/(n-r)!
  • 10P2 =
    10!/(10-2)!
  • 10P2 =
    10!/8!
  • 10P2 =
    10*9*8*7*6.../8*7*6*5*4...
  • 10P2 =
    3 628 800/40 320
  • 10P2 = 90

Ejemplo 3: En una sala de un hospital hay una fila de 4 sillas donde pueden tomar asiento 4 pacientes, donde el orden en el que se sienten definirá el turno de cada uno, entonces ¿De cuantas maneras se pueden repartir los 4 turnos

n = 4 r = 4 4P4 = ?

  • nPr =
    n!/(n-r)!
  • 4P4 =
    4!/(4-4)!
  • 4P4 =
    4!/0!
  • 4P4 =
    4*3*2*1/1
  • 4P4 =
    24/1
  • 4P4 = 24

Ejemplo 4: Si hay un recipiente donde hay 12 papeles, cada uno con una letra distinta y se sacan un total de 5 papeles uno por uno ¿De cuantas formas distintas se pueden sacar?

n = 12 r = 5 12P5 = ?

  • nPr =
    n!/(n-r)!
  • 12P5 =
    12!/(12-5)!
  • 12P5 =
    12!/7!
  • 12P5 =
    12*11*10*9*8.../7*6*5*4*3...
  • 12P5 =
    479 001 600/5040
  • 12P5 = 95 040

Ejemplo 5: En un salón donde estudian 8 estudiantes se recompensará con una medalla a la primera, segunda y tercer mejor nota. Calcular todas las combinaciones posibles.

n = 8 r = 3 8P3 = ?

  • nPr =
    n!/(n-r)!
  • 8P3 =
    8!/(8-3)!
  • 8P3 =
    8!/5!
  • 8P3 =
    8*7*6*5*4.../5*4*3*2*1
  • 8P3 =
    40 320/120
  • 8P3 = 336

Ejemplo 6: Un sistema genera una contraseña automáticamente al presionar un botón, donde la contraseña tiene una longitud de 5 caracteres y hay un total de 20 caracteres disponibles, Ojo no se pueden repetir caracteres una ves ya sean parte de la contraseña, teniendo estos datos, ¿Cuántas contraseñas diferentes se pueden obtener con este algoritmo?

n = 20 r = 5 20P5 = ?

  • nPr =
    n!/(n-r)!
  • 20P5 =
    20!/(20-5)!
  • 20P5 =
    20!/15!
  • 20P5 =
    20*19*18*17*16.../15*14*13*12*11
  • 20P5 =
    2 432 902 008 176 640 000/1 307 674 368 000
  • 20P5 = 1 860 480

Ejemplo 7: Se seleccionará una directiva en un grupo de trabajo, donde los puestos serán: presidente, vicepresidente y secretario, si hay 10 personas en el grupo ¿Cuántas directivas diferentes se pueden formar?

n = 10 r = 3 10P3 = ?

  • nPr =
    n!/(n-r)!
  • 10P3 =
    10!/(10-3)!
  • 10P3 =
    10!/7!
  • 10P3 =
    10*9*8*7*6.../7*6*5*4*3...
  • 10P3 =
    3 628 800/5040
  • 10P3 = 720

Ejemplo 8: Hay una carrera en la que participan 8 corredores, si se les dará una recompensa a los 5 primeros (cada premio será diferente dependiendo de la posición en la que llegaron), entonces ¿de cuántas maneras pueden ser premiados?

n = 8 r = 5 8P5 = ?

  • nPr =
    n!/(n-r)!
  • 8P5 =
    8!/(8-5)!
  • 8P5 =
    8!/3!
  • 8P5 =
    8*7*6*5*4.../3*2*1.
  • 8P5 =
    40320/6
  • 8P5 = 6720

Artículos relacionados

Combinación Probabilidad Probabilidad clásica Probabilidad empirica Probabilidad subjetiva Regla de la suma Regla de la multiplicación Regla del complemento Teorema de bayes Probabilidad total