Trigonometría

Definición de trigonometría

La trigonometría es la rama de las matemáticas y geometría que se encarga del estudio del triángulo (un triangulo es un polígono de 3 lados), este estudio se basa en encontrar las relaciones que existen entre los lados y ángulos de un triangulo, el fin de esto es para poder encontrar lados y ángulos de un triangulo conociendo solamente algunos datos del triangulo.

Caracteristicas principales del triángulo

Los lados de un triangulo, al ser una una medida de longitud se pueden medir en metros, centímetros, etc. Pero para la medición de los ángulos de un triangulo existen 2 opciones muy frecuentes: los radianes y los grados sexagesimales, aunque normalmente en temas de geometría los mas utilizados son los grados.

Dependiendo del triangulo que se este estudiando, existen varias características que varían, pero siempre hay algunas que no importa que tipo de triangulo sea, estas siempre se mantienen, una de ellas es que la suma de los ángulos de un triángulo siempre sera igual a 180, esto resulta muy practico cuando se tienen el valor de dos ángulos del triangulo y se quiere encontrar el tercero, pues al ser la suma de los ángulos 180 lo que se hace es restarle a 180 la suma de los otros ángulos y este será el ángulo que falta, esto puede hacer un proceso mucho mas corto de lo que pudiera ser.

Uso de la trigonometría en otras ramas

El estudio de triángulos es aplicado en temas mucho más complejos que geometría, la trigonometría en general es la base de muchos estudios físicos y matemáticos, por ejemplo, el tema de los vectores en física esta basado 100% en el uso de triángulos y los vectores se ocupan para representar fuerzas, velocidades, aceleraciones, etc. es decir que gran parte de la física utiliza los conceptos que se usan en trigonometría.

Aparte de esto, también tiene una infinidad aplicaciones en la robótica, cada vez que se puede observar un robot moviendo un brazo mecánico o cualquier otro tipo de movimiento del robot, este casi siempre esta basado en triángulos, como podría ser cuantos grados se tiene que abrir un angulo para que el robot llegue a cierta posición, etc.

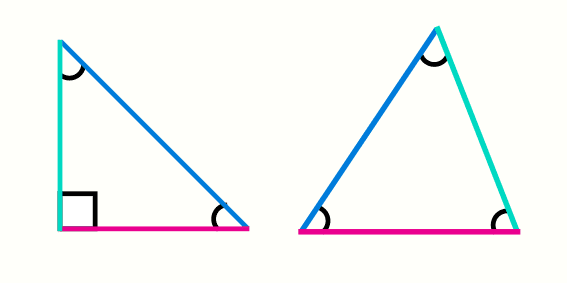
En el estudio de triángulos se pueden clasificar específicamente dos tipos de triángulos: los triángulos rectángulos y los triángulos oblicuángulos, la diferencia en estos dos proviene de sus ángulos, un triangulo rectángulo es aquel que tiene 1 angulo de 90°, mientras que el resto de los triángulos que NO tienen una ángulo de 90° se denominan triángulos oblicuángulos.

Existen varias maneras de clasificar un triangulo, por sus ángulos, por sus lados o por ciertas combinaciones entre ángulos y lados, pero para ramas como la física y matemática la clasificación que se toma en cuenta de un triángulo es si es rectángulo u oblicuángulo

En trigonometría existen varios teoremas y formulas que se han desarrollado con el tiempo para poder encontrar tanto los lados como los ángulos de un triangulo, y hay formulas tanto para triángulos rectángulos como para triángulos oblicuángulos.

Los teoremas que se usan para triángulos rectángulos solamente pueden ser utilizados en triángulos rectángulos, pero las formulas que se usan en triángulos oblicuángulos si se pueden usar para triángulos rectángulos, aunque es mucho mas sencillo usar las formulas correspondientes para cada tipo de triangulo.

A continuación se presentará una corta introducción de los teoremas y leyes principales que existen en la trigonometría.

Teorema de pitágoras (Triángulos rectángulos)

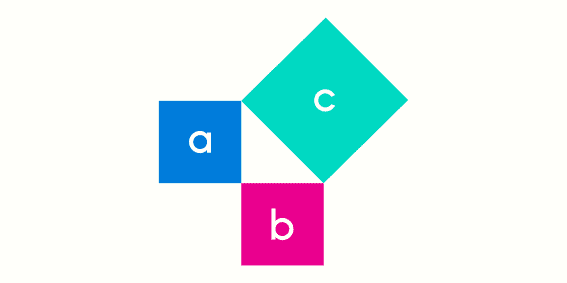
El teorema de Pitágoras permite encontrar un lado de una triangulo rectángulo si se conoce la longitud de los otros 2 triángulos. En este teorema se nombran los lados del triangulo, el lado mas largo (que es el que esta en el lado opuesto al ángulo de 90°) se llama hipotenusa, mientras que los otros 2 lados se les denomina catetos.

El teorema de Pitágoras establece que "la suma de los cuadrados de los catetos será igual a la hipotenusa al cuadrado", este teorema se usa unicamente para encontrar un lado faltante del triangulo, pues este en ningún momento usa ángulos, por lo tanto este teorema se basa exclusivamente en los lados.

Razónes trigonometricas (Triángulos rectángulos)

Las razones trigonométricas son otra forma de resolver un triangulo rectángulo, con la diferencia que este si sirve para encontrar ángulos y lados de un triangulo, estas razones constan de 3 ecuaciones sencillas, estas pueden ser usadas tal y como se establecen más abajo o despejando una ecuación para poder encontrar la variable faltante.

Leyes del seno y coseno (Triángulos oblicuángulos)

Para el caso de los triángulos oblicuángulos, existen 2 ecuaciones, la ley del seno y la ley del coseno, con estas dos leyes se debe analizar cual conviene ocupar para cada situación, porque ambas funcionan para encontrar tanto lados como ángulos de un triangulo oblicuángulo, pero hay ocasiones en la que la mejor opción es ocupar una y no la otra.

Artículos relacionados