Razones trigonométricas
En este artículo Se definirá que son las razones trigonométricas y que es sohcahtoa, para que se ocupa y ejemplos de triangulos.
Definición de Razones trigonométricas
Las razones trigonométricas son ecuaciones que se utilizan para obtener tanto los lados como los ángulos de un triangulo rectángulo, ojo, estas razones solamente se pueden ocupar cuando el triangulo que se quiere resolver tiene un ángulo de 90°.
Estas ecuaciones son útiles en otras ramas aparte de los triángulos, por ejemplo, son útiles para medir distancias entre dos puntos o para hacer operaciones entre vectores o simplemente para trabajar con magnitudes vectoriales, esto porque en física es fácil encontrar triángulos rectángulos en diferentes situaciones, es por eso que es importante aprender a trabajar con triángulos rectángulos y las razones trigonométricas. Por ejemplo en un vector de velocidad, una velocidad al saber su magnitud y sentido se podría descomponer para poder hacer otras operaciones, donde cada componente del vector velocidad es un cateto de un triángulo rectángulo y su magnitud es la hipotenusa.
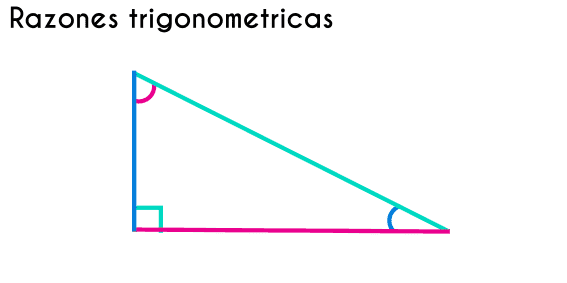
Nombres de lados usados en las razones trigonométricas
Por lo general un triángulo rectángulo se distingue fácilmente porque en la mayoría de las ocasiones el triangulo esta posicionado de manera que hay una línea recta horizontal y otra línea recta vertical y luego hay una línea que une los dos extremos de estas líneas, pero siempre hay que comprobar, porque si un triangulo esta rotado de otra manera entonces ver si tiene un ángulo de 90° es más complicado.
Un triangulo es una figura que simplemente tiene 3 lados, pero en un triángulo rectángulo cada lado tiene un nombre, el lado mas largo del triangulo recibe el nombre de HIPOTENUSA, mientras que a los otros lados dos se les llama CATETOS y son los que forman el ángulo de 90°. Cada cateto puede ser nombrado de dos maneras, “cateto opuesto” y “cateto adyacente” y este sub-nombre se le da a cada uno dependiendo del ángulo del cual se esta tomando como referencia (Ojo, los angulos que tienen catetos opuestos y adyacentes son los que no mide 90°). El lado que esta al a par de un ángulo será el cateto adyacente, mientras que el lado que este en el otro extremo será el cateto opuesto, por eso es importante saber de cual ángulo se esta hablando porque ambos catetos son adyacentes y opuestos, pero son adyacentes de un ángulo y opuestos de otro ángulo. La hipotenusa siempre va a ser el lado mas largo del triángulo y siempre estará en el lado opuesto del ángulo de 90°, que por lo general siempre se va a marcar con un cuadro en el lugar del ángulo.
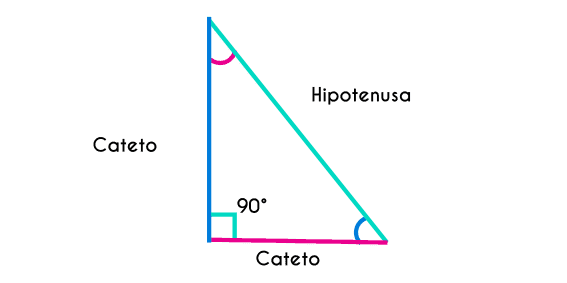
Fórmulas de las razones trigonométricas
Estas fórmulas o ecuaciones son relaciones entre los lados de un triángulo rectángulo y las operaciones seno, coseno y tangente.
- sen(Θ) = Cateto opuestoHipotenusa
- cos(Θ) = Cateto adyacenteHipotenusa
- tan(Θ) = Cateto opuestoCateto adyacente
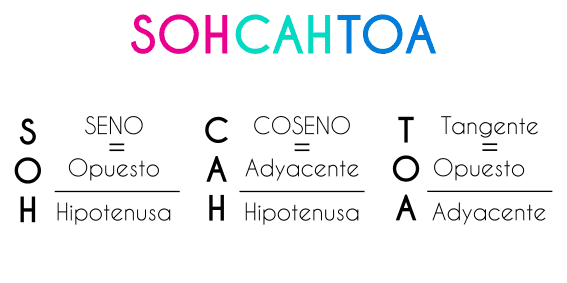
SOHCAHTOA
Aprenderse cada formula puede ser un poco complicado, pero existe una manera de recordarlas y es con la palabra SOHCAHTOA, la palabra se forma de la primera letra de cada variable de cada formula, de la siguiente manera: Seno = Opuesto / Hipotenusa, Coseno = Adyacente / Hipotenusa, Tangente = Opuesto / Adyacente. Es más fácil recordar una palabra a recordar 3 fórmulas, y al recordarla lo único que faltará es desglosar la palabra para recordar la ecuación.
Ejemplos de razones trigonométricas
Ejemplo 1: Encontrar el ángulo "b" del siguiente triángulo, si se sabe que el cateto "A" mide 3 metros y el cateto "B" mide 6 metros
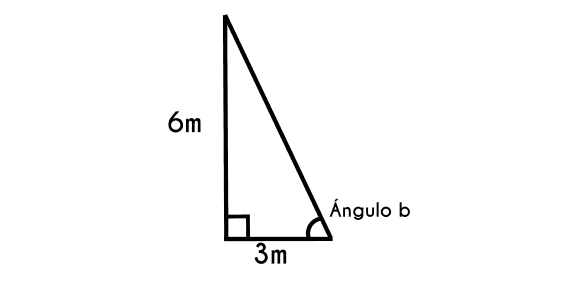
En cada ejercicio se tiene que evaluar los datos que se tienen para saber que fórmula ocupar, en este problema se tienen 2 datos, el cateto b = 6m, y el cateto a = 3m, por lo que se utilizará la siguiente formula
- tan(Θb) = opuestoadyacente
- Primero se despeja el angulo Θb
- Θb = tan-1(opuestoadyacente)
- Θb = tan-1(63)
- Θb = tan-1(2)
- Θb = 63.43°
Ejemplo 2: Se tiene un triangulo que tiene un ángulo de 45° de inclinacion, si se sabe que el cateto opuesto a este ángulo mide 72 centímetros, Hallar el valor de la hipotenusa y del cateto adyacente
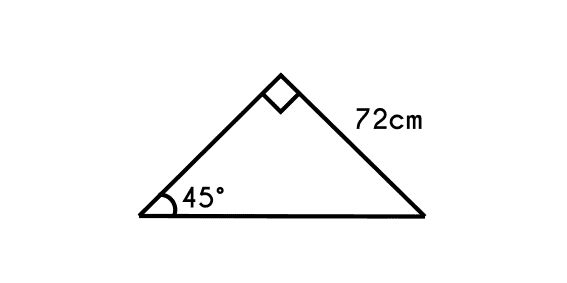
Datos: Lado 1 = 72cm, angulo 1 = 45°
Primero se encontrará el valor del cateto adyacente
- Primero se plantea la fórmula a utilizar
- tan(Θ) = opuestoadyacente
- Ahora se despeja el cateto adyacente
- adyacente = opuestotan(Θ)
- adyacente = 72cmtan(45)
- adyacente = 72cm1
- adyacente = 72 cm
Y por último se encontrara la hipotenusa, que para encontrarla se podría utilizar cualquiera de las otras fórmulas porque se tiene tanto el cateto adyacente como el cateto opuesto
- sen(Θ) = opuestohipotenusa
- Ahora se despeja la hipotenusa
- hipotenusa = opuestosen(Θ)
- hipotenusa = 720.71
- hipotenusa = 101.4cm
Ejemplo 3: Se tiene un triángulo del cual se sabe que la hipotenusa mide 43 metros y tiene un angulo de 31 grados, con estos datos encontrar los dos catetos y el angulo restante
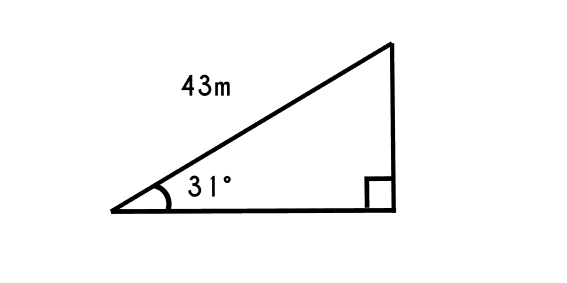
Primero se va a encontrar el cateto adyacente al ángulo de 31°
Datos: angulo a = 31°, hipotenusa = 43 m
- Se encuentra el cateto adyacente
- cos(Θ a) = adyacentehipotenusa
- Se despeja el cateto adyacente
- adyacente = cos(Θ a) * hipotenusa
- adyacente = cos(31) * 43
- adyacente = 0.86 * 43
- adyacente = 36.98
- Se encuentra el cateto opuesto al angulo de 31°
- sen(Θ a) = opuestohipotenusa
- Se despeja el cateto opuesto
- opuesto = sen(Θ a) * hipotenusa
- opuesto = sen(31) * 43
- opuesto = 0.52 * 43
- opuesto = 22.36
Ahora solo falta encontrar el angulo restante, que se podría hacer simplemente restandole a 180 la suma de 31 y 90 que sería más facil, pero se encontrara utilizando las razones trigonometricas
- Se plantea la fórmula a utilizar (se puede utilizar las 3)
- sen(Θ b) = opuestohipotenusa
- Se despeja el ángulo
- Θ b = sen-1(opuestohipotenusa)
- Ojo, el adyacente del angulo a será ahora el opuesto del ángulo b
- Θ b = sen-1(36.9843)
- Θ b = sen-1(0.86)
- Θb = 59.31
Ejemplo 4: Dos hombres parten desde un mismo punto, pero uno comienza a avanzar hacia el norte y otro avanza hacia el este, al cabo de 5 horas, ambos hombres deciden descansar, el que avanzó hacia el norte recorrió un total de 13km mientras que el otro avanzó 10km, ¿Cuál es la distancia a la que se encuentran actualmente?
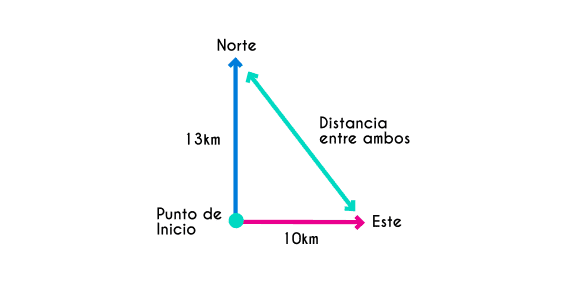
Datos: Cateto A = 13km, Cateto B =10km
Como se puede observar al trazar las distancias que cada uno recorrió se forman los catetos de un triángulo rectángulo donde la distancia que los separa es la hipotenusa del triángulo. No hay ninguna fórmula para encontrar la hipotenusa cuando se tienen los dos catetos, pero si se puede encontrar uno de los ángulos y luego se puede encontrar la hipotenusa
- Se encuentra cualquiera de los angulos, en este caso se encontrará el angulo opuesto al cateto de 13km
- tan(Θ a) = opuestoadyacente
- Se despeja el angulo a
- Θ a = tan-1 (opuestoadyacente)
- Θ a = tan-1 (1310)
- Θ a = 52.43
Ahora con un ángulo resuelto si se puede encontrar la distancia entre los dos hombres (hipotenusa)
- Se plantea la fórmula
- sen(Θ a) = opuestohipotenusa
- Se despeja la hipotenusa(distancia)
- distancia = opuestosen(Θ a)
- distancia = 13sen(52.43)
- distancia = 16.40