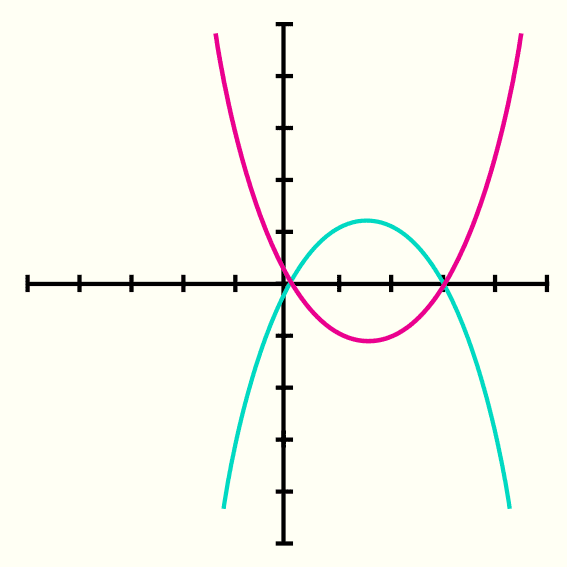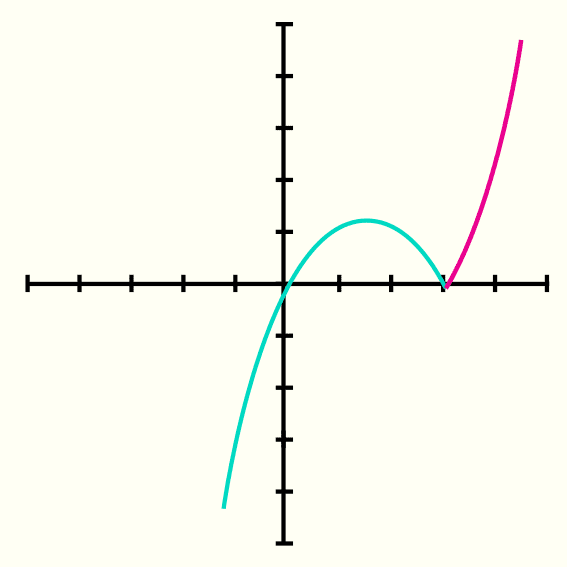Graficar una Función Valor Absoluto
En este articulo se mostrará cómo graficar cualquier tipo de grafica con un valor absoluto con ejemplos de como encontrar las diferentes graficas de diferentes tipos de funciones.
Gráfica de un valor absoluto
Las graficas de las funciones valor absoluto pueden ser muy distintas las unas de las otras y para estas hay 2 formas diferentes de graficarlas, una que es con la definición de la función valor absoluto, y la otra que es la forma general que es evaluando la función y obteniendo las coordenadas por donde pasa la gráfica, en este artículo se mostrarán ejemplos de como graficar las funciones de ambas formas.
Graficar valor absoluto por puntos
La forma más sencilla de graficar el valor absoluto es la de tomar ciertos puntos de “x” y evaluar la función en estos valores de “x” y los resultados de cada valor evaluado serán los valores de “y”, entonces al hacer esto se obtienen las coordenadas (x,y) por donde pasa la función valor absoluto, luego lo que se hace es graficar el plano cartesiano y colocar las coordenadas y posteriormente dibujar una linea que conecte a todos los puntos, y de esta manera se obtiene la gráfica de cualquier función valor absoluto.
Por ejemplo: Realizar la grafica valor absoluto de la función: f(x) = |x - 2| + 1
Lo que se tiene que hacer es formar una tabla donde se obtengan las coordenadas (x,y) por donde pasa la función, esto se hace con una tabla de 3 columnas, una con los valores de "x", otra con la ecuación de la funcion a evaluar, y la tercera con el resultdo de evaluar la función
Los valores de "x" en los que se evaluará la funcion serán desde -5 hasta +5
| x | |x - 2| + 1 | y |
|---|---|---|
| -5 | |-5 - 2| +1 | 8 |
| -4 | |-4 - 2| +1 | 7 |
| -3 | |-3 - 2| +1 | 6 |
| -2 | |-2 - 2| +1 | 5 |
| -1 | |-1 - 2| +1 | 4 |
| 0 | |0 - 2| +1 | 3 |
| 1 | |1 - 2| +1 | 2 |
| 2 | |2 - 2| +1 | 1 |
| 3 | |3 - 2| +1 | 2 |
| 4 | |4 - 2| +1 | 3 |
| 5 | |5 - 2| +1 | 4 |
Ahora teniendo los puntos por donde pasa f(x) = |x-2| + 1 se dibuja el plano cartesiano y se ponen las coordenadas en el y se traza una linea que pase por todos los puntos
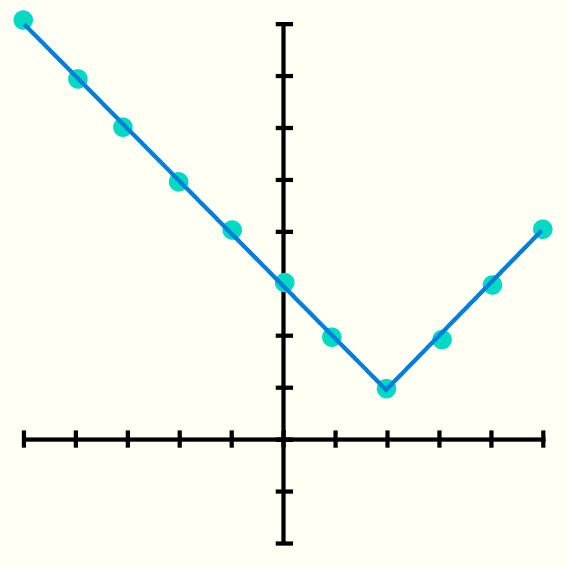
Hay algunas funciones que tienen una forma que no se logra distinguir con claridad con cierta cantidad de puntos, en estos casos se recomienda evaluar la función en valores más pequeños, es decir, que en lugar de evaluar de 1 en 1, evaluar de ½ en ½,o incluso en valores más pequeños porque es posible que evaluando de 1 en 1 no se logre estructurar bien la forma de la función.
Graficar valor absoluto por su definición
La forma anterior es útil para graficar una función valor absoluto de forma más directa, pero esta no siempre es la más efectiva de utilizar cuando se trata de funciones con un mayor grado de dificultad. Cuando se tienen funciones más complejas es más recomendable utilizar la definición de la función.
Toda función con valor absoluto tiene su definición y es la siguiente: por ejemplo para la función f(a) = |a|
- |a| = {
a si a ≥ 0 -a si a < 0
Lo que significa esta definicion es que en la función valor absoluto hay otras 2 funciones, una actúa cuando el valor de “x” es mayor o igual a 0 y la otra cuando el valor de “x” es menor que 0, por ejemplo para la función anterior la función f(a) = a es la función que hay desde 0 hasta mas infinito, mientras que f(a) = -a es la función que está desde menos infinito hasta 0.
Entonces lo que se hace para graficar una función valor absoluto es graficar las dos funciones dependiendo hasta donde la definición lo indique, para demostrar esto se desarrollará el siguiente ejemplo: Graficar la función f(x) = |x - 3| * x
Primero se forma la definción de la función (en la parte del "si a > 0" la parte de "a" es lo que va dentro de del valor absoluto, que en el caso de esta función es x-3):
- |x-3| * x = {
(x-3) * x si x-3 ≥ 0 -(x-3) * x si x-3 < 0
- Primero se despejan las inecuaciones
- |x-3| * x = {
(x-3) * x si x ≥ 3 -(x-3) * x si x < 3
- despues se resuelven los paréntesis que haya
- |x-3| * x = {
x2 -3x si x ≥ 3 -x2 +3x si x < 3
- Cómo se puede observar ahora hay 2 funciones cuadraticas.
Habiendo establecido la definición de la funcion valor absoluto se observa que desde menos infinito hasta 3 será f(x) = -x2 + 3x, y desde 0 hasta mas infinito será f(x) = x2 - 3x, estas son 2 parabolas que pero invertidas, lo que se hace es graficar ambas funciones primero y luego borrar las partes que no pertenezcan a la función valor absoluto.