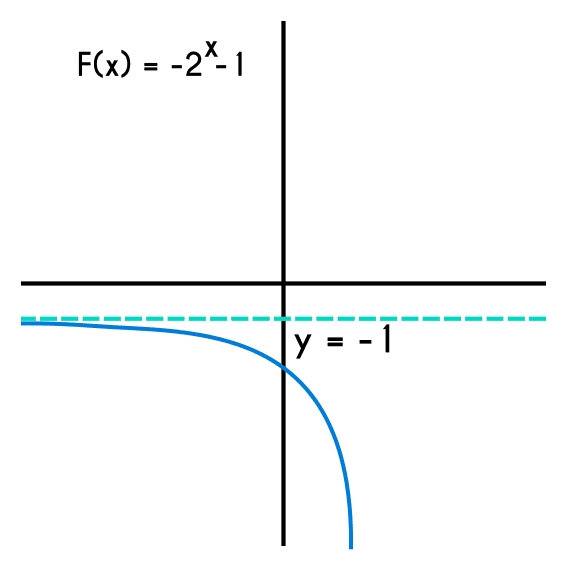Como encontrar el dominio y rango de la Función exponencial
En este articulo se mostrarán los pasos para poder determinar el dominio y rango de la función exponencial con algunos ejemplos para comprender mejor cada concepto.
Una función exponencial se caracteriza por que esta viene pegada a una asíntota horizontal que es el eje de las “x”, una asíntota horizontal es un punto en “x” que la función nunca toca pero siempre se irá aproximando a ella, pero mientras esta función va avanzando esta va creciendo a un ritmo cada vez mayor.
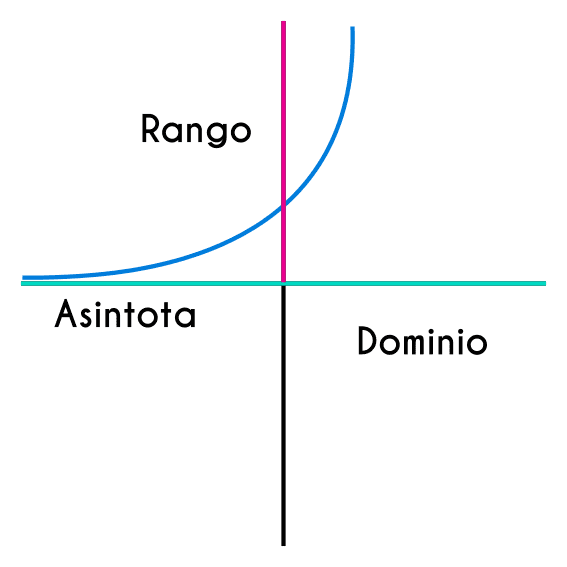
Dominio y rango de una función exponencial
Ahora conociendo como se comporta la función exponencial se puede definir el dominio y el rango de esta misma, el dominio de cualquier función exponencial es siempre los reales, es decir, que es cualquier número entre menos infinito y más infinito ]-∞, +∞[.
En el caso del rango la cosa cambia un poco, porque como se puede observar en la definición anterior, el rango no son todos los reales, porque la grafica viene creciendo desde el eje de las “x”, es decir cuando "y" es igual a 0 hasta el infinito, entonces esto representado en intervalos sería ]0, +∞[, importante saber que el corchete de 0 es abierto porque la grafica se aproxima lo máximo posible a 0 pero jamas lo toca, por lo tanto el 0 no es parte del rango de la función.
Lo anterior es el dominio y rango para la función que tiene la forma f(x) = ax, pero esto cambia un poco cuando se tiene una función tipo f(x) = ax + b. El dominio en estas funciones continua siendo el mismo, lo que cambia es el rango, porque en esta ocasión el valor de “b” es la asíntota horizontal de la función, por lo que el rango de la función será desde b hasta infinito.
Otra factor que define el rango de una función exponencial es el signo de la variable “a”, si “a” es positiva entonces la función va a crecer desde la asíntota hasta más infinito, de lo contrario, si “a” es negativa entonces la función crecerá desde la asíntota hasta menos infinito.
Entonces teniendo en cuenta los 2 factores anteriores se puede definir el dominio y rango de una función exponencial, por ejemplo, para la función f(x) = 3x-1, el dominio como siempre son los reales, en cuanto al rango, como se puede ver el valor de la variable “b” es -1, que este representa el valor de la asíntota, y como el valor de “a” es positivo entonces significa que el rango de la función ira desde -1 hasta más infinito.
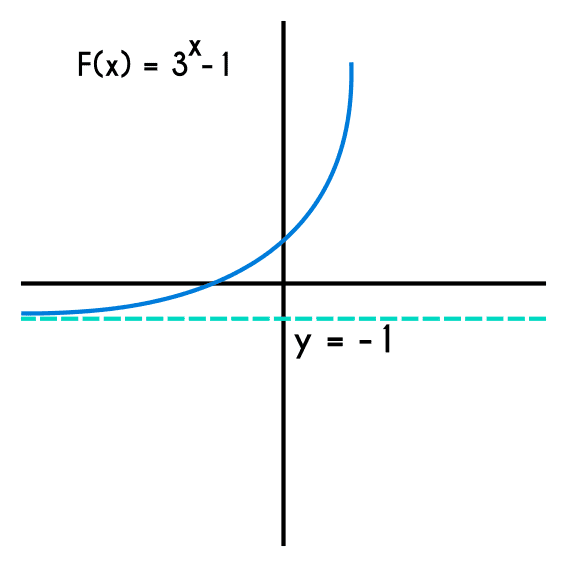
Ejemplos de dominio y rango exponencial
Ejemplo 1: Encontrar el dominio y rango de la función f(x) = 5x + 10
Como el 5 es positivo entonces el rango de la función será desde la asíntota hasta más infinito, y como la variable "b" esta en y=10 entonces el rango será desde 10 hasta más infinito, y el dominio son los reales
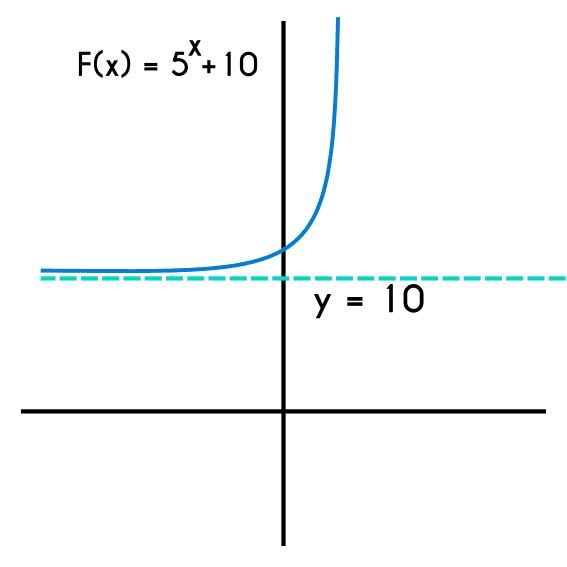
Ejemplo 2: Definir el dominio y rango de la función f(x) = -2x - 1
En este caso la variable "a" es negativa, por lo que la funcion crecerá desde la asíntota que está en y=-1 hasta menos infinito, por lo tanto el rango va desde -1 hasta menos infinito, y el dominio como siempre son los Reales