Sum of matrices, step by step with examples.
This article will be about How to sum matrices of any type of order, guide step by step and examples.
A matrix is an array of numbers or a set of numbers, where the numbers are ordered in rows and columns, the special thing about a matrix is they way they are ordered, there are an infinity types of matrices, the types of matrices are classified depending on the order they have, the order of the matrix matters when we want to operate two matrices, where for each operation there are some conditions that the matrices have to meet.
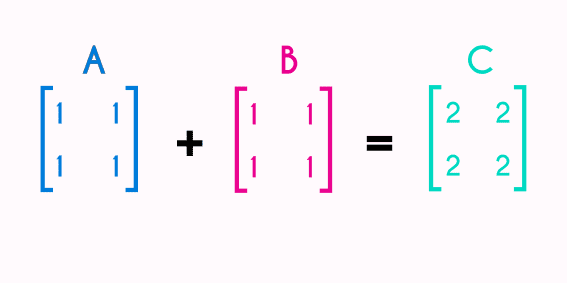
In case of the sum of matrices, the condition is that the matrices must have the same order, otherwise they cannot be added, for example, if the 2 matrices have a 4x4 order (that have 4 columns and 4 rows) or if both matrices are 2x1 (that have 2 rows and one column) these can be summed, but if we have a 2x3 matrix and 3x1 matrix, these two cannot be added.
The sum of matrices consist in adding the numbers that are in the same position in the matrices we are adding and the result of the sum of each position will be the same position in the resultant matrix.
Sum of two matrices (3x2)
To exemplify how to sum 2 matrices we are going to sum the following matrices.
Matrix A
| 2 | 8 |
| 4 | 10 |
| 6 | 12 |
Matrix B
| 3 | 12 |
| 6 | 15 |
| 9 | 18 |
To differentiate each position of the matrix we are going to use the following method: Mrc where M is the name of the matrix (normally we use a letter), “r” is the row and “c” is the column where the number is located, this way we can define the position of each number inside the matrix, for example, the number A32 is referring to the number that is in the row 3 and column 2 of the matrix A.
Now that we know this we are going to sum the positions of the matrices to obtain the same positions in the resultant matrix.
We sum the matrices
| 2 + 3 | 8 + 12 |
| 4 + 6 | 10 + 15 |
| 6 + 9 | 12 + 18 |
We get the C matrix
| 5 | 15 |
| 10 | 25 |
| 15 | 30 |
Example of the sum of matrices
Example 1: What is the resultant matrix of the sum of the following matrices.
Matriz a
| -2 | 1 |
| -4 | -3 |
Matriz b
| 6 | -5 |
| 3 | 2 |
Now the following step is sum every position of the matrix and that way find the resultant matrix.
We make the sum
| -2 + 6 | 1 + (-5) |
| -4 + 3 | -3 + 2 |
Matrix c
| 4 | -4 |
| -1 | -1 |
Example 2: Sum the following matrices of 4x3 order.
Matrix E
| 1 | 2 | 3 |
| 4 | 5 | 6 |
| 7 | 8 | 9 |
| 10 | 11 | 12 |
Matrix T
| 2 | 4 | 6 |
| 8 | 10 | 12 |
| 14 | 16 | 18 |
| 20 | 22 | 24 |
We make the sum
| 1 + 2 | 2 + 4 | 3 + 6 |
| 4 + 8 | 5 + 10 | 6 + 12 |
| 7 + 14 | 8 + 16 | 9 + 18 |
| 10 + 20 | 11 + 22 | 12 + 24 |
Result matrix
| 3 | 6 | 9 |
| 12 | 15 | 18 |
| 21 | 24 | 17 |
| 30 | 33 | 36 |
Example 3: Add the following matrices 5x3.
Matrix a
| 4 | 3 | 1 |
| 2 | 4 | 6 |
| 2 | 1 | -7 |
| 7 | 2 | 9 |
| 2 | 2 | 2 |
Matrix b
| 4 | 0 | 3 |
| 0 | 6 | 0 |
| 5 | 1 | 6 |
| -5 | -1 | 3 |
| -4 | -2 | 0 |
We make the sum
| 4 + 4 | 3 + 0 | 1 + 3 |
| 2 + 0 | 4 + 6 | 6 + 0 |
| 2 + 5 | 1 + 1 | -7 + 6 |
| 7 + (-5) | 2 + (-1) | 9 + 3 |
| 2 +(-4) | 2 + (-2) | 2 + 0 |
Resultant matrix
| 8 | 3 | 4 |
| 2 | 10 | 6 |
| 7 | 2 | -1 |
| 2 | 1 | 12 |
| -2 | 0 | 2 |
Example 4: What is the resultant matrix of following sum 6x3.
Matrix a
| 12 | 9 |
| 20 | -18 |
| 0 | 13 |
| 1 | 2 |
| -2 | 9 |
| -21 | 23 |
Matrix b
| 42 | 31 |
| 12 | 33 |
| 92 | 56 |
| -50 | 21 |
| 49 | 76 |
| 1 | 23 |
We make the sum
| 12 + 42 | 9 + 31 |
| 20 + 12 | -18 + 33 |
| 0 + 92 | 13 + 56 |
| 1 + (-50) | 2 + 21 |
| -2 + 49 | 9 + 76 |
| -21 + 1 | 23 + 23 |
Resultant matrix
| 54 | 40 |
| 32 | 15 |
| 92 | 69 |
| 49 | 23 |
| 47 | 85 |
| 20 | 46 |