Multiplication of matrices by scalars, with Examples
This article will be about how to multiply a matrix by a scalar, with examples, and a step by step guide of how to make this types of multiplications.
How to multiply a matrix by a scalar
A matrix is a set or array of numbers, which has a determined order, this means that has an established mount of rows and columns, while a scalar is just a number that does not needs anything else to be expressed, when we are talking about a scalar, we are referring to an integer, decimal, rational or irrational number (A real number), it could positive or negative.
Although a matrix and a scalar are totally different things, we can make some operations between them, one of this operations is the multiplication between a matrix and a scalar.
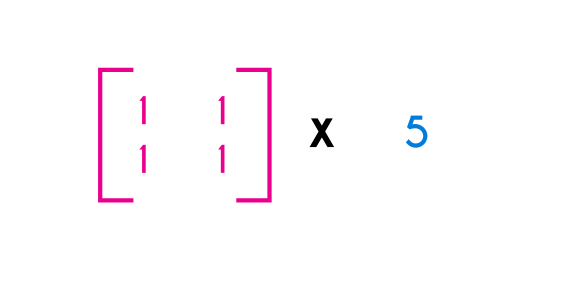
As we know, a matrix is a set of numbers ordered in rows and columns, so the multiplication of a matrix by a scalar consist in multiplying the scalar number “k” (a real number or a constant, we are calling it “k”) by each position in the matrix, and the result will be a matrix that has the same amount of rows and columns as the multiplied matrix, for example, if we have a matrix named A, and this has a 2x4 order, and if this matrix is multiplied by a constant “k”, the result will be a matrix with same order as A (2 rows and 4 columns) but with every position of the matrix multiplied by “k”.
This multiplication is done by multiplying every element of the matrix by “k” (being k a real number) respecting the position of each element and the matrix order.
Matrix A
| A11 | A12 |
| A21 | A22 |
The result of multiplying A by K would be every element of A by k, just as we can see in the next matrix.
| K * A11 | K * A12 |
| K * A21 | K * A22 |
In the multiplication between a matrix and a scalar, the distributed property is also a thing, for example, if we have two matrices, one of them called A and the other one called “B”, and if we have a constant called K, and we make the following operation: K(A + B), this would be the same as K(A) + K(B).
When we multiply a matrix by a scalar, most of the time we have to make the every multiplication inside the matrix to get the resultant matrix, but there are some values of “k” that allows us to know the result just by following the multiplication properties when it comes to a matrix by a scalar.
One of this properties is when the number multiplying the matrix is 0, when the scalar is equals to 0, then the result will be a null matrix, we call a null matrix when all the values inside the matrix are equals to 0, but even when all the values are equals to 0, the order of the matrix will be the same, for example if we multiply a 3x3 matrix by 0, the result would be a null matrix with 3 rows and 3 columns.
0 * A
| 0 | 0 |
| 0 | 0 |
Another property of the multiplication of a matrix by a scalar is when the scalar is equals to -1. In this case, just like the previous situation, the quantity of rows and columns will be the same, the difference here is that every element inside the matrix will have the same value but with the opposite sign, for example, if one of the elements inside the matrix is -4, then this element in the resultant matrix would be: -1 * (-4) = 4.
Examples of mulitplying a scalar by a matrix
Example 1: If we have the following matrix
| 2 | 1 |
| 4 | 2 |
Solve : -4 * A
First we multiply every element of the matrix by -4
| -4 * 2 | -4 * 1 |
| -4 * 4 | -4 * 2 |
An we solve the multiplications
| -8 | -4 |
| -16 | -8 |
Example 2: Multiply the following matrix by 0
| 5 | -3 |
| 9 | 2 |
| 7 | 10 |
As we said before when multiplying a matrix by 0 we would have a matrix with the same mount of rows and columns but with all the element equals to 0 like this:
| 0 * 5 | 0 * -3 |
| 0 * 9 | 0 * 2 |
| 0 * 7 | 0 * 10 |
| 0 | 0 |
| 0 | 0 |
| 0 | 0 |
Example 3: If we have the following 2x2 matrix
| 0 | -1 |
| 3 | -9 |
| 1 | -3 |
Solve : 6 * A
Every time we multiply, we have to be very carefull with the signs, we have to apply the sign law correctly so we do not have any mistake with the results
| 6 * 0 | 6 * (-1) |
| 6 * 3 | 6 * (-9) |
| 6 * 1 | 6 * (-3) |
| 0 | -6 |
| 18 | -54 |
| 6 | -18 |
Related articles