Subtraction of matrices explained step by step
This article will be about The subtraction of matrices, we are going to explain how to do it, with examples explained step by step.
How to subtract matrices
Before we try to subtract two or more matrices we have to understand one thing first, and is that we can only subtract matrices that have the same order, this means that the matrices need to have the same amount of columns and rows, for example, to subtract a 3x1 matrix (3 rows and 1 column) we could only subtract it with another 3x1 matrix.
Cleared that up, we can now proceed to subtract matrices, first it is necessary to understand how to locate a number by its position in columns and rows, the way we name every position is the following way: A23 where A is the name given to the matrix, the first number (2) is the row number where the number is positioned, and the second number (3) is the column number where the number is located.
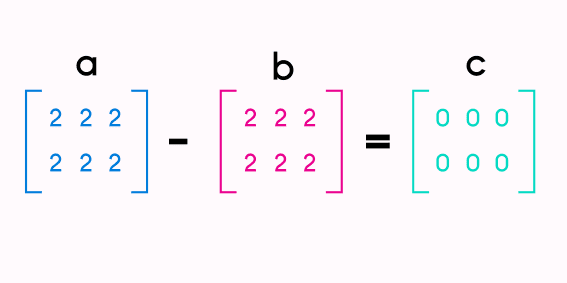
Subtraction of two matrices 3x2
The subtraction is done by subtracting the numbers in the same positions in both of the matrices, and the answer of that will be the number in the same position in the resultant matrix, like this: A22 - B22 = C22.
It is really important to clarify that the difference between the sum and the subtraction of matrices, is that in this case, the order of the matrices matters, for example in a sum of matrices is the same to say A + B than say B + A, because we would get the same answer, but in subtraction of matrices, A-B and B-A is not the same, this two procedures are going to give us different answers, so we have to be careful when we set the matrices.
That said, we are going to subtract the following matrices
Matrix A
| 2 | 1 |
| 5 | 6 |
| 2 | 9 |
Matrix B
| 3 | 6 |
| 8 | 1 |
| 7 | 0 |
We write the subtraction of every position
Matrix without solving
| 2-3 | 1-6 |
| 5-8 | 6-1 |
| 2-7 | 9-0 |
Result
| -1 | -5 |
| -3 | 5 |
| -5 | 9 |
Example of matrix subtraction
Example 1: Subtract the following two matrices
Matrix A
| 4 | 12 | -5 |
Matrix B
| -3 | 1 | 9 |
We write the subtractions
| 4-(-3) | 12-1 | -5-9 |
Resultant Matrix
| 7 | 11 | 14 |
Example 2: Subtract A - B
Matrix A
| 3 | 5 |
| 8 | 6 |
| 9 | 1 |
| 4 | 9 |
Matrix B
| 7 | 7 |
| -5 | -5 |
| 0 | 0 |
| 3 | 3 |
We subtract every position
| 3-7 | 5-7 |
| 8-(-5) | 6-(-5) |
| 9-0 | 1-0 |
| 4-3 | 9-3 |
Resultant Matrix
| -4 | -2 |
| 13 | 11 |
| 9 | 1 |
| 1 | 6 |
Example 3: Subtract the matrices of 2x2 order
Matrix A
| 12 | -13 |
| -52 | 43 |
Matrix B
| -71 | -90 |
| -42 | -27 |
Write the subtraction of each position
| 12-(-71) | -13-(-90) |
| -52-(-42) | 43-(-27) |
Resultant matrix
| 83 | 77 |
| -10 | 70 |
Example 4: Solve the following subtraction A-B
Matrix A
| 4 | -21 | 0 |
| 98 | 2 | 73 |
Matrix B
| 44 | 1 | 88 |
| 3 | 56 | 5 |
We write the subtractions
| 4-44 | -21-1 | 0-88 |
| 98-3 | 2-56 | 73-5 |
Resultant matrix
| -40 | -22 | -88 |
| 95 | -54 | 68 |