Sum 3x3 matrix, with examples
This article will be about The sum of 3x3 matrices, explained step by step with various examples.
How to sum a 3x3 matrix
A matrix with a 3x3 order has 3 rows and 3 columns, and we can only sum a 3x3 matrix with another matrix with the same order, otherwise we are not able to sum them. In this article we will develop some examples of the sum of this kind of matrices, if what we explain in the following paragraph is not that clear, please go the example section below to practice what we explained.
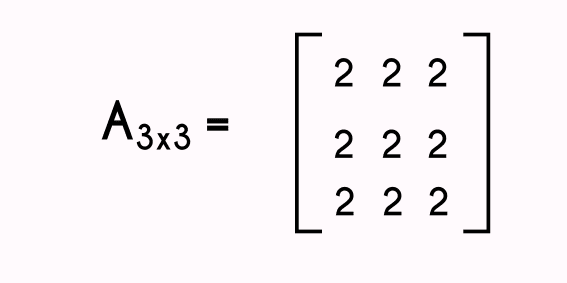
When we sum two matrices with a 3x3 order, we have to sum every number inside the matrices with the same position of the other matrix, this means that to find the number (in the resultant matrix) in the row 3, column 3, we are going to have to sum the numbers in the row 3 and column 3 of both of the matrices we are adding, and the result of that will be our answer, this process written would be like this: A23 B23 = C23, being A and B the matrices we are adding, and C the resultant matrix, and once we have done all 9 positions of the 3x3 matrix, we already would have the resultant matrix.
Examples of sum of 3x3 matrix
Example 1: Sum A + B
Matrix A
| 3 | -2 | 6 |
| 1 | 7 | 9 |
| -3 | 4 | 2 |
Matrix B
| 8 | 1 | 3 |
| -6 | 1 | 1 |
| 2 | 1 | 7 |
First we write the sum
| 3+8 | -2+1 | 6+3 |
| 1+(-6) | 7+1 | 9+1 |
| -3+2 | 4+1 | 2+7 |
Resultant matrix
| 11 | -1 | 9 |
| -5 | 8 | 10 |
| -1 | 5 | 9 |
Example 2: Sum the following 3x3 matrices
Matrix A
| -1 | -4 | -5 |
| -1 | -9 | 0 |
| 2 | 7 | -2 |
Matrix B
| 3 | 12 | 2 |
| 3 | 7 | 5 |
| 8 | 9 | 0 |
Write every position sum
| -1+3 | -4+12 | -5+2 |
| -1+3 | -9+7 | 0+5 |
| 2+8 | 7+9 | -2+0 |
Resultant Matrix
| 2 | 8 | -3 |
| 2 | -2 | 5 |
| 10 | 16 | -2 |
Example 3: Find the resultant matrix of the following sum
Matrix A
| 0 | 1 | 0 |
| 0 | 1 | 0 |
| 0 | 1 | 0 |
Matrix B
| 1 | 0 | 1 |
| 1 | 0 | 1 |
| 1 | 0 | 1 |
We sum the positions.
| 0+1 | 1+0 | 0+1 |
| 0+1 | 1+0 | 0+1 |
| 0+1 | 1+0 | 0+1 |
Resultant matrix
| 1 | 1 | 1 |
| 1 | 1 | 1 |
| 1 | 1 | 1 |
Example 4: What is the result of the sum of the matrices A + B
Matrix A
| 33 | 21 | 12 |
| 44 | 31 | 9 |
| 91 | 72 | 2 |
Matrix B
| 21 | 90 | 10 |
| 11 | 31 | 13 |
| 24 | 63 | 61 |
We sum the positions
| 33+21 | 21+90 | 12+10 |
| 44+11 | 31+31 | 9+13 |
| 91+24 | 72+63 | 2+61 |
Resultant Matrix
| 54 | 111 | 22 |
| 55 | 62 | 22 |
| 115 | 135 | 63 |
Example 5: Solve the sum of the following 3x3 matrices
Matrix A
| 7 | 3 | 4 |
| 2 | 9 | 6 |
| 1 | 2 | -20 |
Matrix B
| 3 | 8 | 8 |
| 11 | 5 | 9 |
| 15 | 15 | 38 |
We write the positions
| 7+3 | 3+8 | 4+8 |
| 2+11 | 9+5 | 6+9 |
| 1+15 | 2+15 | -20+38 |
Resultant Matrix
| 10 | 11 | 12 |
| 13 | 14 | 15 |
| 16 | 17 | 18 |
Example 6: ¿What is the resultant matrix of the sum of the following 3x3 matrices?
Matrix A
| -21 | -1 | -3 |
| -1 | -62 | -12 |
| -98 | -22 | -90 |
Matrix B
| 14 | 67 | 91 |
| 72 | 14 | 0 |
| 2 | 1 | 3 |
We sum every position
| -21+14 | -1+67 | -3+91 |
| -1+72 | -62+14 | -12+0 |
| -98+2 | -22+1 | -90+3 |
Resultant Matrix
| -7 | 66 | 88 |
| 71 | 48 | -12 |
| 96 | -21 | 87 |