Sum of matrix of 2x2 order with examples
This article will be about the sum of 2x2 matrices, with examples step by step.
Sum or addition of 2x2 matrix
A matrix with a “2x2” order means that it will have two rows and two columns, and we can only sum a 2x2 matrix with another matrix or matrices with the same order. in this article we are going to show how to sum 2x2 matrices.
| 2 | 2 |
| 2 | 2 |
The sum is done by summing every number of the first matrix with every number that is in the same position in the second matrix, for example in a 2x2 matrix we sum the number of the first row and first column of the first matrix with the number in the first row and the first column in the second matrix, and the answer will be the position column one and row one of the resultant matrix: A11 + B11 = C11 and we have to do this with every position in the matrix, and this is how we sum 2x2 matrices.
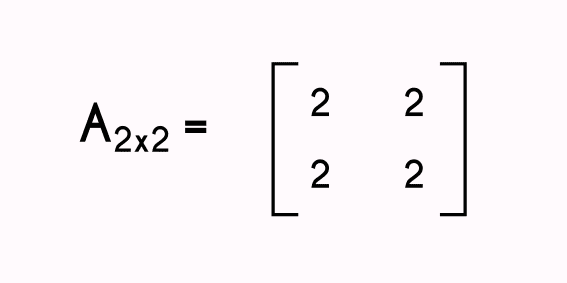
Examples of 2x2 matrix
Example 1: Sum the following matrices
Matrix A
| 1 | 1 |
| -1 | -1 |
Matrix B
| 2 | 2 |
| -2 | -2 |
Sum the positions
| 1 + 2 | 1 + 2 |
| -1 + (-2) | -1 + (-2) |
Resultant matrix
| 3 | 3 |
| -3 | -3 |
Example 2: Sum A + B
Matrix A
| 12 | 22 |
| 37 | 45 |
Matrix B
| 13 | 41 |
| 29 | 18 |
Sum the positions
| 12 + 13 | 22 + 41 |
| 37+ 29 | 45 + 18 |
Resultant matrix
| 25 | 63 |
| 66 | 63 |
Example 3: Calculate the resulting matrix of the folloing sum
Matrix A
| 109 | 133 |
| -121 | 123 |
Matrix B
| 222 | 123 |
| -33 | 0 |
Sum of every position
| 109 + 222 | 133 + 123 |
| -121 + (-33) | 123 + 0 |
Resultant matrix
| 331 | 256 |
| -154 | 123 |
Example 4: Sum the following matrices
Matrix A
| 472 | 297 |
| 366 | 500 |
Matrix B
| 528 | 703 |
| 634 | 500 |
Sum of positions
| 472 + 528 | 297 + 703 |
| 366 + 634 | 500 + 500 |
Resultant matrix
| 1 000 | 1 000 |
| 1 000 | 1 000 |
Example 5: Sum the A + B matrices
Matrix A
| 421 | 90 |
| 102 | 31 |
Matrix B
| -421 | -90 |
| -102 | -31 |
Sum of positions
| 421 + (-421) | 90 + (-90) |
| 102 + (102) | 31 + (-31) |
Resultant matrix (In this case the resulting matrix is a null matrix, it means that every position of the matrix will be equals to 0)
| 0 | 0 |
| 0 | 0 |
Example 6: Sum of matrices
Matrix A
| -32 | 21 |
| -17 | 0 |
Matrix B
| 1200 | -321 |
| 1 | -200 |
Sum of positions
| -32 + 1200 | 21 + (-321) |
| -17 + 1 | 0 + (-200) |
Resultant matrix
| 1168 | -300 |
| -16 | -200 |