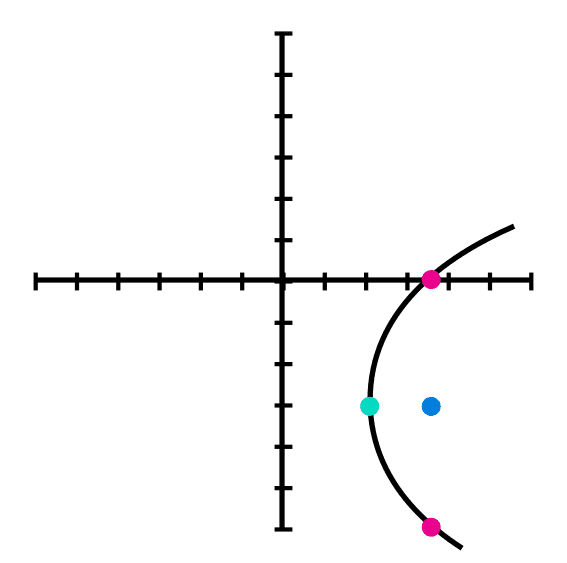
La ecuación canónica de una parábola
En este artículo Se mostrará como es la ecuación canónica de una parábola, como usarla para graficar una parábola y como entender cada parte de la ecuación, con ejemplos.
Qué es la ecuación canonica de una parábola
La ecuación canónica de una parábola es una manera de escribir y describir los principales aspectos de una parábola. Sabiendo interpretar una ecuación canónica de manera correcta se puede llegar a conocer algunas de las características más importantes en una parábola, por ejemplo, simplemente con ver la estructura de la ecuación que se plantea se puede saber hacia dónde abre la parábola o donde está posicionado el vértice, y luego para saber las coordenadas del foco o el valor del parámetro (p) simplemente basta con hacer unas cuantas operaciones sencillas para tener todos los datos que permiten graficar una parábola.
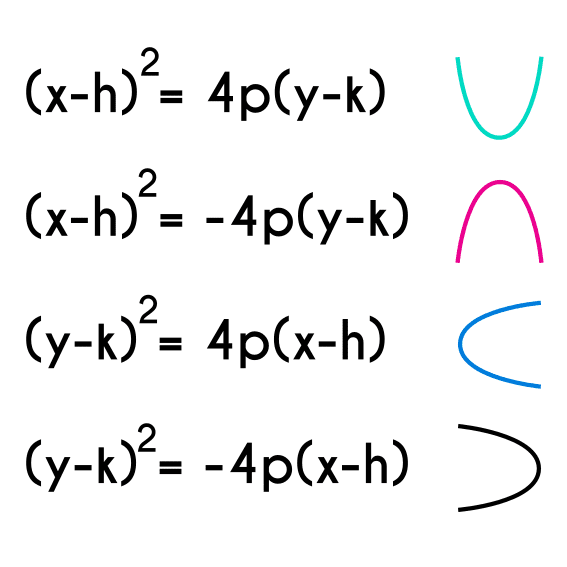
Estructura de la ecuación canonica
Todas las ecuaciones que están en la imagen anterior son ecuaciones canónicas de parábolas, pero cada una tiene algunas cosas que varían, como el orden de las variables o algunos signos, y estos pequeños cambios son los que provocan que haya parábolas que apunten hacia la derecha, izquierda, arriba y abajo, como se puede observar en la imagen. A continuación se explicará como reconocer de que tipo de parábola es una ecuación.
Saber la dirección de una parábola
Cuando una ecuación tiene elevado al cuadrado el paréntesis que contiene a la variable “x”, entonces es una parábola vertical, es decir, que la parábola abre hacia arriba o hacia abajo (es decir que esta es una función), pero si por el contrario el paréntesis que está al cuadrado es el que contiene a la variable “y”, entonces la parábola es horizontal, es decir, que la parábola abre hacia la derecha o hacia la izquierda.
Apertura de una parábola
Ahora bien, para saber con exactitud hacia donde es la apertura de la parábola hay que ver el signo de “4p”, si el signo de “4p” es positivo entonces la parábola abrirá hacia los números positivos, es decir, que si es una parábola vertical abrirá hacia arriba y si es una parábola horizontal abrirá hacia la derecha, y si “4p” es negativo (-4p) entonces la parábola abrirá hacia los números negativos, es decir, que si es una parábola horizontal abrirá hacia la izquierda y si es una parábola vertical esta abrirá hacia arriba.
Por ejemplo: la parábola que se da por la ecuación (x - 3)2 = -4(y+4) es una parábola que se abre hacia abajo, (y+4) 2 = 4(x - 3) es una parábola que abre hacia la derecha. De esta manera ya se puede saber la dirección de la parábola simplemente con mirar la ecuación canónica.
Vertice en la ecuación canonica
Como se puede observar en las ecuaciones también están las variables “h” y “k”, como ya se sabe estas variables son las coordenadas (x,y) del vértice de la parábola, el vértice es el punto máximo o mínimo de la parábola (dependiendo de hacia dónde se abre) y este siempre está en el centro de la parábola y es quizás el punto más importante de una parábola y con la ecuación canónica se puede conocer la coordenada del vértice, pero ojo, a los valores que tienen “h” y “k” en la ecuación hay que cambiarles el signo, si es negativo hay que pasarlo a positivo y viceversa, esto porque en la ecuación canónica el signo anterior a “h” y “k” es negativo, entonces esto hace que tengan el signo contrario.
Un truco para recordar cual es “h” y cuál es ” k” es que “h” siempre estará en el paréntesis de “x” y “k” siempre estará en el paréntesis de “y”.
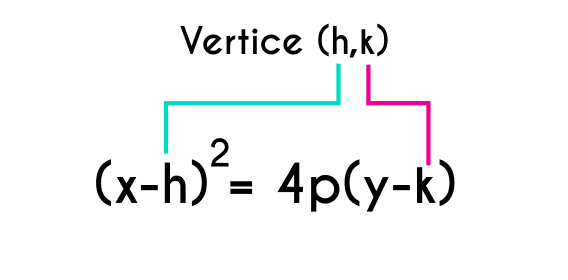
Por ejemplo: en la ecuación (x - 3) = 2(y+4) 2 el vertice esta en (3,-4) y en (x +6) 2 = 9(y-1) el vertice esta en (-6,1).
Parámetro en la ecuación canónica
Este es la distancia que hay entre el foco y el vértice y entre el vértice y la directriz, y se representa por la letra “p”, y este si está explícitamente en la ecuación canónica, lo único que está representado como “4p” lo que quiere decir que el número que este allí será igual a 4 veces el valor de “p” por lo tanto, para encontrar el valor genuino de “p” se debe dividir ese número entre 4.
Por ejemplo: en la ecuacion (x -3) 2 = 12(y+3): en la posición de “4p” está el numero 12, así que para encontrar “p” se divide 12/4 y el resultado de esto es 3, por lo que “p” vale 3. Ahora bien, el valor de la línea recta es 4 veces p, por lo que en este caso el valor de la línea recta sería 12.
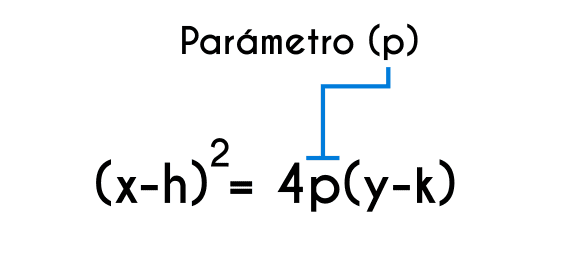
Ahora explicado cada parte de la ecuación lo único que falta es ponerlo en práctica, para ello se graficarán diferentes parábolas a través de una ecuación canónica.
Ejemplos de la ecuación canónica
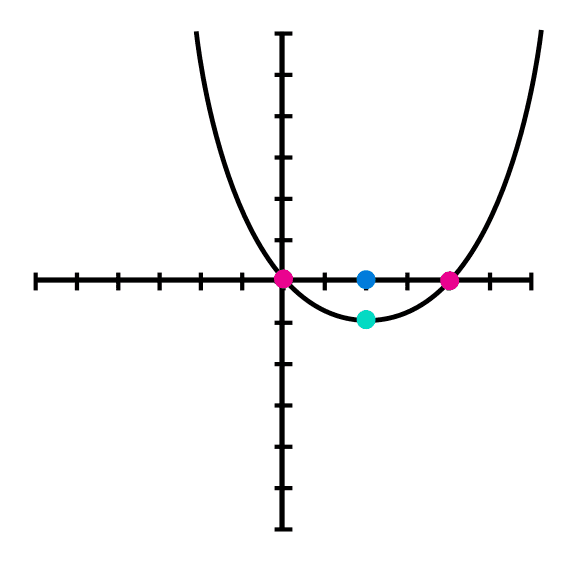
Ejemplo 1: graficar la siguiente parábola: (x-2)2 = 4(y+1)
Apertura de la parábola: hacia arriba.
Posicion del vértice: (2,-1) recordar que los signos de h y k cambian de como están en la fórmula.
Valor del parámetro: el valor de 4p es 4, por lo que para encontrar "p" se divide 4/4 = 1.
coordenadas del Foco: (2,0), como el valor de p es 1 y la parabola se abre hacia arriba, el foco estará un número por encima del vértice.
Linea recta: la linea recta es de 4, por lo que se extenderá 2 números a cada lado del foco, porque esta pasa justo por encima del foco y en los extremos de la linea recta es donde pasa la parábola, y con estos datos se puede graficar la parábola.
Ejemplo 2: grafica: (y+3)2 = 6 (x-2)
Apertura de la parábola: hacia la izquierda
Posicion del vértice: (2,-3)
Valor del parámetro: 1.5
coordenadas del Foco: (3.5,-3)
Linea recta: 6