Puntos de corte de una Función Cuadrática
En este articulo se mostrará cada paso a realizar para encontrar donde corta con cada eje una función cuadrática
Para encontrar los puntos de corte de una función cuadrática se debe tener claro 2 condiciones, la primera es que para que una función corte con el eje “y” la “x” tiene que ser igual a 0, y la segunda es que para que una función corte con el eje “x” el valor de “y” debe ser igual a 0, asi como se puede observar en la siguiente imagen.
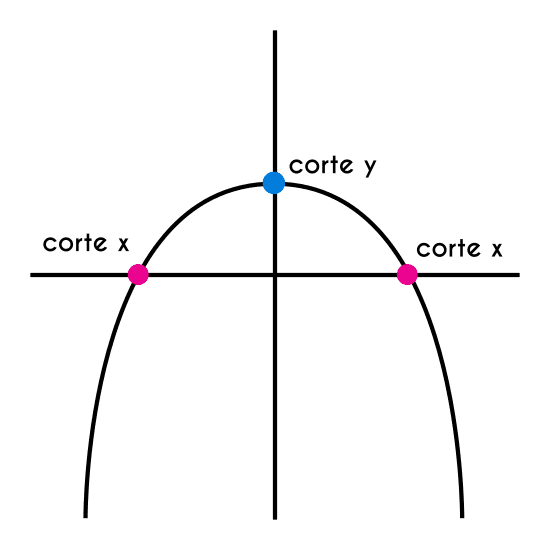
Ahora comprendiendo cuando se da cada punto de corte, estas son las fórmulas y procesos que se utilizarán para poder encontrar cada punto de corte.
Punto de corte con el eje “y”: se obtiene simplemente evaluando la función cuando “x” es igual a 0, una función cuadrática siempre cortará con el eje “y” aunque en ocasiones esta llega a cortar con “y” en un punto muy elevado o muy bajo pero siempre se llega a una respuesta.
Por ejemplo: Encontrar el punto de corte con el eje "y" en la función f(x) = x2 -2x
- f(x) = x2 -2x
- f(0) = (0)2 -2(0)
- f(0) = 0-0
- f(0) = 0
Punto de corte con el eje “x”: Una función cuadrática tiene 3 variantes con el corte con el eje “x”, la primera opción es que la función corte con el eje “x” 2 veces, la segunda variante es cuándo la parábola corta con el eje x pero solo una vez (esto es cuando el vértice está justo sobre el eje “x” (h=0,k) ), y el tercer escenario es cuando la función nunca corta con el eje “x”, en la práctica se puede saber cuando la función cuadrática no corta con el eje “x” porque se llega a un procedimiento que no se puede resolver, este siempre será la raíz de un número negativo, pues no se puede encontrar la raíz cuadrática de un número negativo.
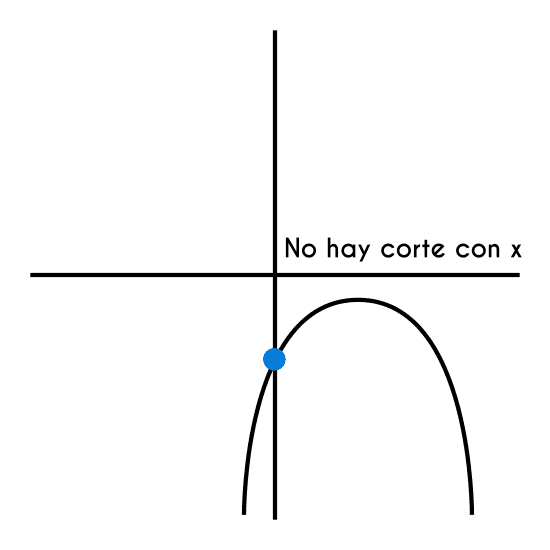
Estos se obtiene igualando la función a 0 y despejando a “x”, pero despejar “x” de una ecuación que tiene una “x” al cuadrado y otra "x" elevada a la 1 no es algo sencillo como pasar las letras de un lado a otro y por este motivo hay más de una manera de resolver estas ecuaciones, quizás la más complicada pero la que siempre dará una respuesta es utilizando la formula cuadrática, también hay otros casos donde se puede factorizar la ecuación cuadrática pero esto no siempre se puede realizar, por eso es que es mejor utilizar la formula cuadrática. En caso de que la función no tenga una "x" a la 1, entonces este proceso se haría simplemente despejando "x2" y en estos casos solo habría 1 punto de corte con el eje "x".
Encontrar puntos de corte con la formula cuadrática: cuando se encuentran los puntos de corte con el eje “x” los pasos a seguir son: ordenar la función de la manera ax2 + bx + c, e introducir los datos en la ecuación, luego resolver hasta llegar a las dos soluciones.
- Fórmula cuadrática
- x =-b ± √ (b2 - 4ac)2a
Por Ejemplo: encontrar el punto de corte con el eje “x” de la función f(x) = 2x2 + 3x + 1.
- x = -3 ± √(32 - 4(2)(1) )2(2)
- x = -3 ± √(9 - 8)4
- x = -3 ± √14
- x = -3 ± 14
- Se encuentra x1
- x = -3 + 14
- x = -24
- x = -0.5
- Se encuentra x2
- x =-3-14
- x =-44
- x = -1
- Los puntos de corte con "x" son: (-1, 0) y (0.5, 0)
Encontrar puntos de corte factorizando: Lo que se hace aquí es buscar 2 números que sumados den el segundo término y multiplicados den el tercer término, pero en ocasiones no hay manera de encontrar estos números, ya sea porque sean decimales u otro caso.
Por ejemplos: encontrar el punto de corte con el eje “x” de f(x) = 2x2 - 2x - 12. Una condición de esta factorización es que el coeficiente del primer término tiene que ser igual a 1, pero en este ejemplo el coeficiente del primer término es 2, entonces se debe convertir este 2 en 1 dividiendo todos los términos entre 2.
- Lo primero que hay que hacer es hacer el coeficiente del primer término 1, para ello se tiene que dividir el término entre 2, pero para mantener la igualdad se hará esto con todos los términos
-
2x22-2x2-122= 0
- x2 - x - 6 = 0
- Ahora se encuentran dos numeros que sumados den el segundo termino (-1) y multiplicado den el tercero (-6)
- Estos números son 2 y -3, porque:
- 2 + (-3) = 2-3 = -1
- 2 * -3 = -6
- Entonces estos se agregan a dos binomios igualados a 0:
- (x + 2) (x - 3) = 0
- Ahora lo que se hace es igualar cada binomio a 0 y despejar la "x"
- Solución para x1
- x+2 = 0
- x = -2
- Solución para x2
- x - 3 = 0
- x = 3
Ejemplos de puntos de cortes
Ejemplo 1: Encontrar los puntos de corte con los ejes de la función f(x) = 2x2 + 3x - 4
- Corte con eje "y"
- f(0) = (0)2 + 3(0) - 4
- f(0) = 0 + 0 - 4
- f(0) = - 4
- Corte con eje "x"
- Se hará con la fórmula cuadrática
- x = -b ± √ (b2 - 4ac)2a
- x = -3 ± √ (32 - 4(2)(-4) )2(2)
- x = -3 ± √ (9 +32 )4
- x = -3 ± √ (41)4
- x = -3 ± 6.44
- Solución para x1
- x1 = -3 + 6.44
- x1 = 3.44
- x1 = 0.85
- Solución para x2
- x1 = -3 - 6.44
- x1 = -9.44
- x2 = 2.35
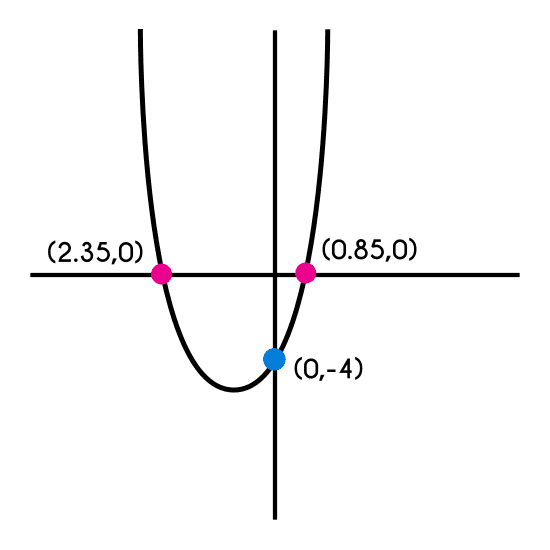
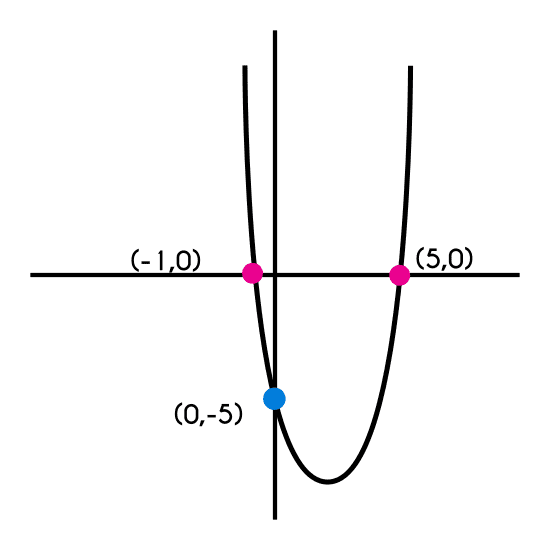
Ejemplo 2: Definir el corte con "x" y "y" de la función f(x) = x2 - 4x - 5
Esta función se resolverá factorizando
- Corte con el eje "y"
- f(0) = 02 + 4(0) - 5
- f(0) = 0 - 0 - 5
- f(0) = - 5
- x2 - 4x - 5
- Como el coeficiente del primer termino ya es 1 simplemente se pasa a factorizar
- Se encuentran dos numeros que sumados den -4 y multiplicados den -5
- -5 y 1
- -5 + 1= 4
- -5 * 1= -5
- Por lo tanto se forman los dos binomios
- (x-5) (x+1) = 0
- Se igualan a 0 ambos binomios
- x-5 = 0
- x = 5
- y
- x+1 = 0
- x = -1
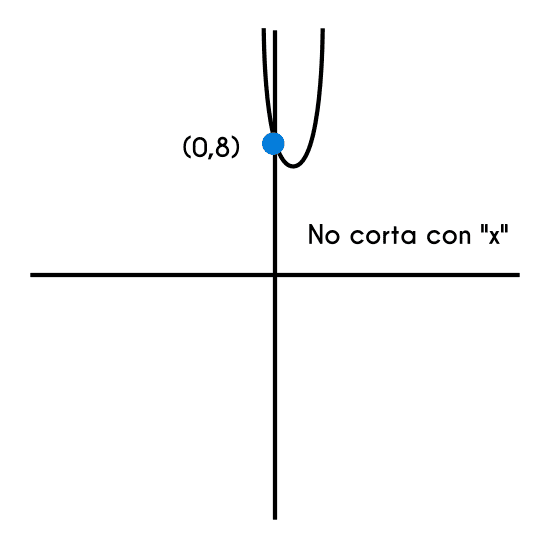
Ejemplo 3: ¿Cuáles son los puntos de corte con los ejes de la función f(x) = 3x2 - 5x + 8 ?
- Corte con el eje "y"
- f(0) = 3(0)2 - 5(0) +8
- f(0) = 0 - 0 + 8
- f(0) = 8
- 3x2 - 5x + 8
- Se plantea la fórmula cuadrática
- x = -(-5) ± √ (-52 - 4(3)(8) )2(3)
- x =5 ± √ (25 - 96 )6
- x =5 ± √ (-71)6
- Como se observa esta operacion no se puede seguir realizando, porque no se puede encontrar la raíz cuadrada de un número negativo, entonces esta función no tiene cortes con el eje "x"