Pasos para graficar una función cuadrática con ejemplos
En este artículo Se mostrarán los pasos a seguir para graficar la parábola de una función cuadrática, con ejemplos.
¿Cómo graficar una función cuadrática?
Para graficar una función cuadrática lo primero que se debe hacer es analizar la función, pues la parábola de una función cuadrática puede abrir o hacia arriba o hacia abajo, y esto se puede ver explícitamente en la ecuación de la función. Otra cosa que se debe encontrar antes de graficar es la ubicación del vértice, porque a partir de este se van a ir encontrando puntos por donde pasa la gráfica de la función cuadrática.
Todo lo que se explica en los siguientes párrafos se llevará a la practica en los ejemplos que están más abajo, en caso de no entender una parte de los pasos, se recomienda ir a los ejemplos para tener una mejor comprensión
Pasos para graficar una función cuadrática
Lo primero que se debe hacer cuando se quiere graficar una función cuadratica es encontrar el vértice, porque la fórma en la que se graficarán las funciones cuadráticas en este artículo será evaluando la función en ciertos valores de “x”, pero es importante que los números en los que se evalúe la función sean números que estén alrededor de la posición del vértice, porque de esta manera la parábola quedará centrada y se podrá capturar justo cuando la función baja y vuelve a subir, o sube y vuelve a bajar, dependiendo de la dirección de la parábola, si esto no se hace es muy probable que quede una gráfica que sea simplemente una curva que vaya hacia arriba o hacia abajo. Hay otras maneras de graficar una función cuadrática, todas son validas pero la forma que se hará aqui es la más directa.
Entonces, aclarado lo anterior se tiene que encontrar el vértice, como ya se sabe, la forma de la función cuadrática es ax2 + bx + c, donde el valor de “a” es el número que está acompañado por “x2”, “b” es el valor del número que acompaña a la “x” y “c” es el valor que está solo, ojo, en ocasiones la función cuadrática no esta ordenada de tal manera, es por esto que hay que saber encontrar a, b y c independientemente del orden que tenga la función.
- Fórmula para encontrar el vértice
- x = -b2a
Cuando ya se tiene ubicado la coordenada “x” del vértice, el siguiente paso es evaluar la función en donde está ubicado el vértice y los valor que están alrededor de este, por ejemplo, si el vértice esta en x=2, entonces se evaluarían los valores de x=0, 1, 2, 3 y 4. Esto se hace así porque cuando se grafica una función lo importante es graficar la parte donde la parábola sube y baja, si esto no se hace y se toman valores de “x” al azar es muy probable que al graficar la función quede una línea un poco curvada que vaya hacia arriba o hacia abajo, que no significa que esta no esté mal y que esta no sea la gráfica de la parábola, pero no es la parte importante de la parábola.
Para evaluar los datos en la función, la forma más ordenada es ubicar los datos que se obtengan en una tabla que luzca más o menos asi:
| x | 0 | 1 | 2 | 3 | 4 |
|---|---|---|---|---|---|
| y |
Y una vez teniendo esto lo siguiente será dibujar un plano cartesiano, y luego colocar los puntos que se sacaron en la tabla, una vez realizado esto lo siguiente será dibujar una línea un tanto curvada que pase por todos estos puntos, hecho esto ya se tendría la gráfica de cualquier función cuadrática.
Una cosa que ayuda a comprobar si se graficó bien la función es ver el signo que tiene la variable "a", pues si esta variable tiene un signo negativo esto indica que la parábola abrirá hacia abajo y si el signo es positivo entonces la función abrirá hacia arriba.
Ejemplos de cómo graficar
Ejemplo 1: graficar la funcion f(x)= x2 + 2x + 1
Como se muestra en la explicación anterior, lo primero que se hará es encontrar la coordenada “x” del vértice, para ello se ponen los valores de a, b y c de la función: a=1, b=2 y c=1 .
- Se encuentra el vertice
- x = -b2a
- x = -(2)2(1)
- x = -22
- x = -1
Ahora conociendo donde está el vértice lo siguiente es evaluar la función en números alrededor de este, por ejemplo -3, -2, -1, 0 y 1
- cuando x = -3
- f(-3)= (-3)2 + 2(-3) + 1
- f(-3)= 9 - 6 + 1
- f(-3) = 4
- cuando x = -2
- f(-2)= (-2)2 + 2(-2) + 1
- f(-2)= 4 - 4 + 1
- f(-2) = 1
- cuando x = -1
- f(-1)= (-1)2 + 2(-1) + 1
- f(-1)= 1 - 2 + 1
- f(-1) = 0
- cuando x = 0
- f(0)= (0)2 + 2(0) + 1
- f(0)= 0 + 0 + 1
- f(0) = 1
- cuando x = 1
- f(1)= (1)2 + 2(1) + 1
- f(1)= 1 + 2 + 1
- f(1) = 4
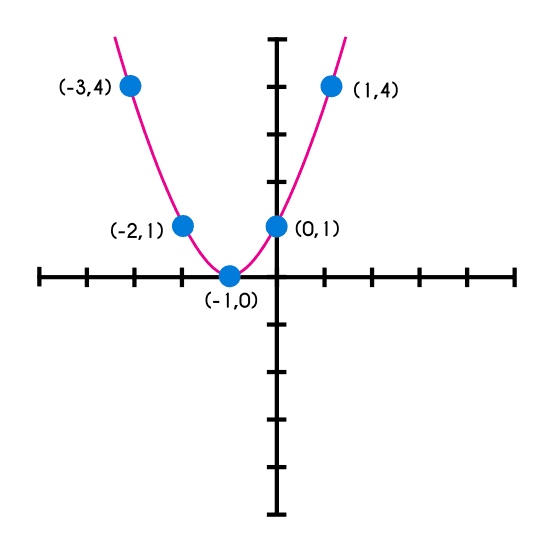
| x | -3 | -2 | -1 | 0 | 1 |
|---|---|---|---|---|---|
| y | 4 | 1 | 0 | 1 | 4 |
Por ultimo se dibujan los puntos en el plano cartesiano y se traza una línea que conecte a todos los puntos.
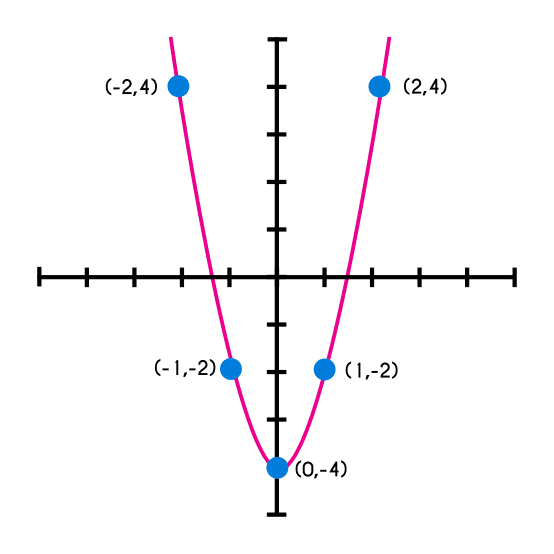
Ejemplo 2: graficar la funcion f(x)= 2x2 -4. Ojo, como no hay un numero acompañando a una "x" se intuye que el valor de "b" es 0 (este ejemplo se desarrollará mas directamente)
- Primero se encuentra el vertice
- x = -b2a
- x = -(0)2(2)
- x = 04
- x = 0
Los números en los que se evaluará la funcion serán -2, -1, 0, 1 y 2
| x | -2 | -1 | 0 | 1 | 2 |
|---|---|---|---|---|---|
| y | 4 | -2 | -4 | -2 | 4 |
Ahora solamente falta poner los puntos por donde pasa la grafica y unir estos puntos.