Movimiento rectilíneo uniformemente variado (MRUV).
En este artículo exploraremos las características clave del movimiento rectilíneo uniformemente variado (MRUV), cuándo se manifiesta, y cómo identificarlo. Además, proporcionaremos una serie de ejemplos ilustrativos y una variedad de ejercicios resueltos utilizando las fórmulas que se presentarán en las secciones siguientes.
Definición mruv
El movimiento rectilíneo uniformemente variado (MRUV), también conocido como movimiento rectilíneo uniformemente acelerado (MRUA), es un tipo de movimiento que se caracteriza por su trayectoria en línea recta y una aceleración constante distinta de cero. En este tipo de movimiento, la velocidad cambia de manera uniforme en función de la dirección de la aceleración.
Características principales del MRUV: Para identificar un movimiento rectilíneo uniformemente variado, es necesario comprender sus parámetros clave:
- Su trayectoria es lineal, lo que significa que se desplaza en una sola dimensión.
- La aceleración es distinta de cero, lo que lo diferencia de un movimiento rectilíneo uniforme (MRU).
- La velocidad varía de manera constante debido a la aceleración, lo que implica que siempre trabajaremos con una velocidad inicial y una velocidad final en problemas relacionados con el MRUV.
Unidades y Dimensiones en el MRUV
En el contexto del Movimiento Rectilíneo Uniformemente Variado (MRUV), es esencial comprender las unidades y dimensiones que se utilizan para medir las diferentes cantidades físicas involucradas. Las unidades de medida clave en el MRUV incluyen metros (m) para la distancia, segundos (s) para el tiempo y metros por segundo al cuadrado (m/s²) para la aceleración. Estas unidades son muy importantes para expresar las magnitudes físicas de manera coherente y realizar cálculos precisos. Además, es crucial tener en cuenta las dimensiones de estas cantidades, que son longitud (L) para la distancia, tiempo (T) para el tiempo y longitud por tiempo al cuadrado (L/T²) para la aceleración. Comprender las unidades y dimensiones en el MRUV es esencial para aplicar las ecuaciones correctamente y comprender la relación entre las variables físicas en este tipo de movimiento.
Papel de la Gravedad en el MRUV
En el estudio del Movimiento Rectilíneo Uniformemente Variado (MRUV), es importante comprender el papel que desempeña la gravedad en los objetos en movimiento. En la Tierra, la aceleración debida a la gravedad se establece en aproximadamente 9.81 metros por segundo al cuadrado (m/s²). Esta aceleración constante es de suma importancia en los problemas de caída libre, donde un objeto se desplaza verticalmente bajo la influencia exclusiva de la gravedad, sin que ninguna otra fuerza relevante intervenga. La aceleración causada por la gravedad es una constante esencial en la física y se utiliza para calcular la velocidad y la posición de los objetos en caída libre a lo largo del tiempo. Esto implica que, en ausencia de fuerzas adicionales, cualquier objeto en la Tierra experimentará una aceleración hacia abajo de aproximadamente 9.81 m/s² debido a la gravedad. Esta aceleración se incorpora en las ecuaciones del MRUV para describir con precisión la caída libre y otros movimientos sujetos a aceleración vertical.
Diferencia entre un MRUV y un MRU
La diferencia principal entre el MRU y el MRUV radica en la presencia de aceleración. En el MRUV, la aceleración está presente, lo que significa que la velocidad no es constante a lo largo de todo el movimiento. Por lo tanto, siempre habrá una velocidad inicial y una velocidad final en el MRUV. La aceleración representa el cambio constante en la velocidad durante un período de tiempo determinado. Los signos o la dirección de tanto la aceleración como la velocidad pueden proporcionar información sobre la naturaleza del movimiento. Si ambas magnitudes tienen el mismo signo (y, por lo tanto, la misma dirección), el objeto en movimiento seguirá avanzando y acelerando en esa dirección. Sin embargo, si los signos de la velocidad y la aceleración son opuestos (por ejemplo, una aceleración negativa y una velocidad positiva), se cancelarán mutuamente, lo que eventualmente llevará al cuerpo en movimiento a detenerse.
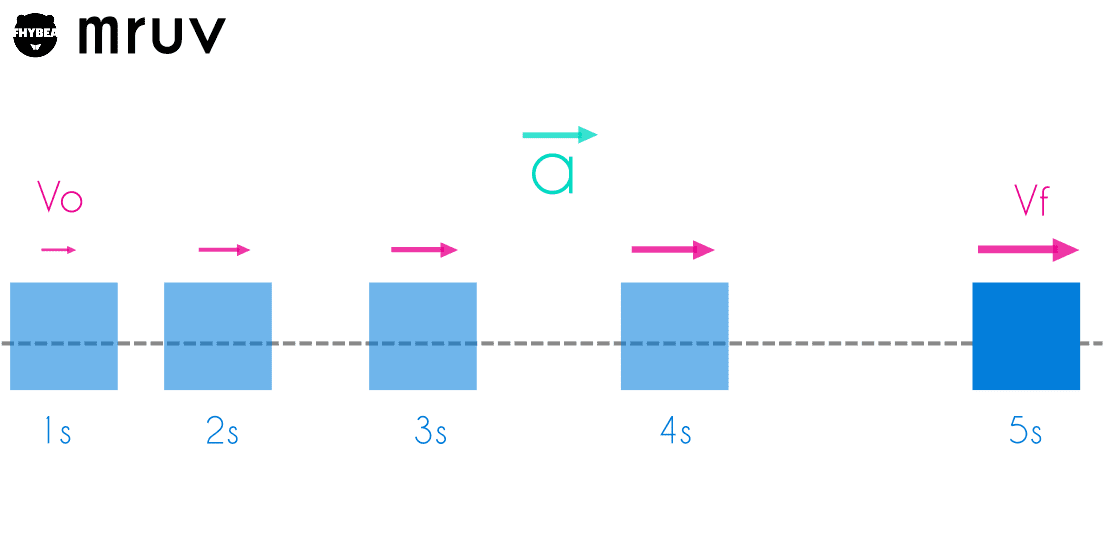
MRUV con aceleración positiva y velocidad inicial nula
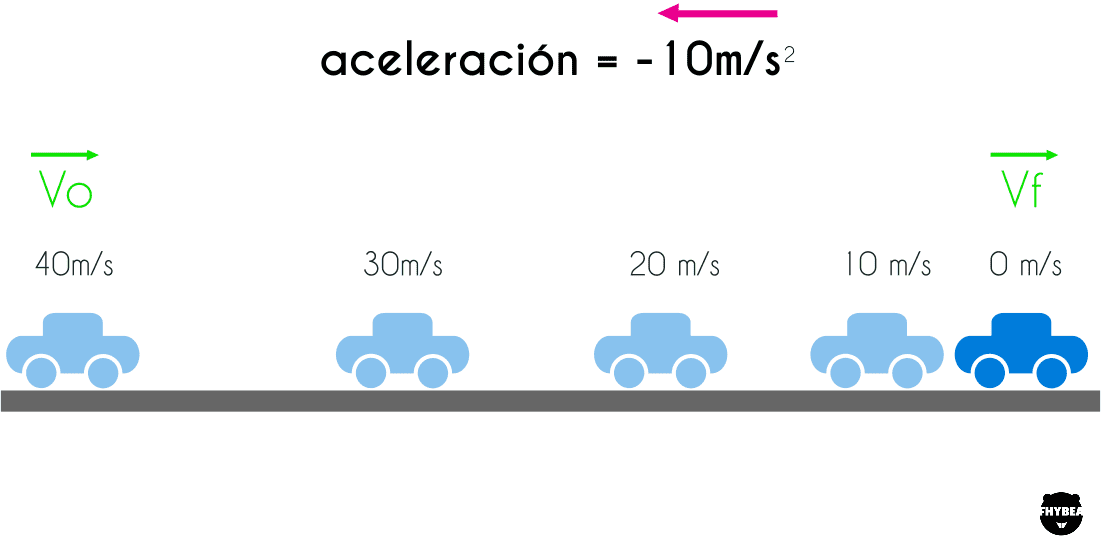
MRUV con aceleración negativa y velocidad inicial positiva
Comportamiento de un Movimiento Rectilíneo Uniformemente Variado
En un sistema de referencia convencional, se suele considerar que las direcciones hacia arriba y hacia la derecha son positivas, mientras que las direcciones hacia abajo y hacia la izquierda se consideran negativas. Por lo tanto, si un objeto experimenta un movimiento rectilíneo uniformemente variado (MRUV) comenzando desde el reposo y se le aplica una aceleración positiva, se desplazará hacia la derecha en el plano cartesiano. En contraste, si la aceleración aplicada es negativa, el móvil se moverá hacia la izquierda en el plano cartesiano.
Cuando un objeto en movimiento rectilíneo uniformemente variado experimenta una aceleración en dirección opuesta a su velocidad actual, entonces su velocidad comenzará a disminuir hasta que el objeto finalmente quede en estado de reposo. Después de ese punto, el objeto comenzará a moverse en la dirección opuesta. Un ejemplo de este comportamiento es el tiro vertical, que ocurre cuando se lanza un objeto hacia arriba. El tiro vertical es una variante del MRUV, y como se puede observar, cuando lanzamos algo hacia arriba, llega un momento en el que el objeto deja de ascender, parece quedarse inmóvil y luego comienza a descender.
Fórmulas del MRUV
Existen cinco fórmulas o ecuaciones para resolver problemas y ejercicios relacionados con el movimiento rectilíneo uniformemente variado (MRUV). Estas fórmulas son versátiles y pueden utilizarse para encontrar diferentes variables en distintas situaciones. La clave está en saber cuál de ellas aplicar en función de los datos proporcionados en un ejercicio específico, ya que en algunos casos, los datos no coinciden exactamente con los parámetros de una fórmula específica. Por lo tanto, es esencial seleccionar la fórmula que mejor se adapte a la situación dada.
Donde: Vo = velocidad inicial, Vf = velocidad final, a = aceleración, d = distancia recorrida
- vf = vo + a * t
- d = vo * t + 1/2 * a * t2
- vf2 = vo2 + 2 * a * d
- vo2 = vf2 - 2 * a * d
- d = Vo + Vf2* t
En un ejercicio en el que se te solicite encontrar la velocidad final de un objeto y se proporcionen la velocidad inicial, la aceleración y la distancia, la primera fórmula no será adecuada ya que requiere el tiempo como dato. En ese caso, la tercera fórmula es la más apropiada, ya que utiliza exactamente los datos proporcionados. Pero, ¿cómo funciona este enfoque?
Imagina que tienes un objeto en movimiento, y te dan la velocidad inicial (Vo), la aceleración (a) y la distancia recorrida (d), pero no te proporcionan directamente el tiempo (t). La primera fórmula, que relaciona la velocidad final (Vf) con Vo, a y t, parece incompleta en este escenario. Entonces, ¿qué hacemos?
En lugar de buscar directamente la velocidad final, puedes aprovechar la tercera fórmula, que relaciona Vf, Vo, a y d. Esta fórmula no requiere el tiempo como dato, lo que la hace más útil en este caso. Comenzarás resolviendo la tercera fórmula para encontrar la velocidad final (Vf).
Una vez que hayas calculado Vf utilizando la tercera fórmula, habrás encontrado un valor importante en tu problema. A continuación, puedes utilizar la primera fórmula, que relaciona Vf, Vo, a y t, para encontrar el tiempo (t). Ahora tienes todos los datos necesarios para resolver completamente el problema y determinar la velocidad final del objeto en movimiento.
Este enfoque demuestra la versatilidad de las fórmulas del MRUV. Aunque una fórmula específica puede no encajar perfectamente con los datos proporcionados, puedes combinar diferentes fórmulas para obtener la solución completa. Es importante comprender cómo cada fórmula se relaciona con las variables para elegir la estrategia más adecuada en cada situación de resolución de problemas.
Gráficos de un Movimiento Rectilíneo Uniformemente Variado (MRUV)
Gráfico posición-tiempo (p-t)
El gráfico de posición-tiempo (p-t) en un MRUV representa la posición del objeto en función del tiempo. Por lo general, este gráfico toma la forma de una parábola vertical, con la parte positiva de la parábola representando el movimiento del objeto en la dirección positiva. La pendiente de la curva p-t indica la velocidad instantánea del objeto, mientras que el área bajo la curva en un intervalo de tiempo específico representa la distancia recorrida por el objeto durante ese intervalo.
Gráfico velocidad-tiempo (v-t)
El gráfico velocidad-tiempo (v-t) en un MRUV es un gráfico lineal en el que la velocidad del objeto se representa en el eje vertical y el tiempo en el eje horizontal. La pendiente de esta gráfica es igual a la aceleración del movimiento, ya que la velocidad cambia de manera uniforme en el MRUV. Observar el gráfico v-t es una forma efectiva de determinar si la aceleración es constante o varía en el tiempo.
Gráfico aceleración-tiempo (a-t)
El gráfico aceleración-tiempo (a-t) en un MRUV es una gráfica constante, ya que la aceleración en este tipo de movimiento es uniforme y constante. La aceleración se representa en el eje vertical y el tiempo en el eje horizontal. La recta horizontal en este gráfico indica que la magnitud de la aceleración no cambia durante el movimiento y es constante en el tiempo.
Resuelve cualquier problema de mruv con nuestra calculadora!
Calculadora mruvEjemplos de MRUV
A continuación unos ejemplos de movimientos que tienen las características de un mruv
Entre parentesis si pertenece a un movimiento derivado del mruv
- Un coche de carrera que acelera desde cero
- Lanzar un objeto hacia arriba (tiro vertical)
- Dejar caer una piedra desde cierta altura (caída libre)
- Una camioneta en movimiento de que frena para desacelerar hasta quedar en estado de reposo
- Un avión que aumenta su velocidad progresivamente
- Una persona que acelera el pasó constantemente hasta correr
- Un tren que frena al llegar a la estación
Ejercicios Mruv
En la resolución de problemas de mruv casi siempre hay más de una ecuación que puede servir para poder llegar a un resultado, por eso antes hay que evaluar que ecuación conviene utilizar para que no se complique tanto resolver el problema. También hay que ser cuidadoso con los datos que no se dan en el problema y elegir esa ecuación a la que le falte esa variable.
Ejercicios resueltos
Datos que da el ejercicio Datos a encontrar
Ejercicio 1: Un vehículo que está en reposo empieza a acelerar a razón de 2 m/s, si este continua con esta aceleración durante 10 segundos ¿Que velocidad alcanzara a los 10 segundos?
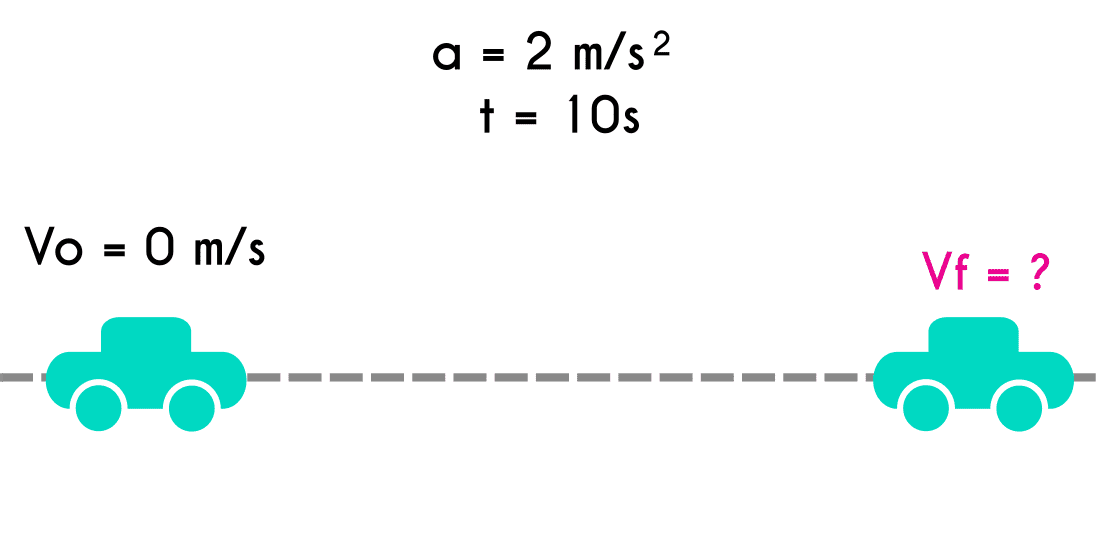
Datos del ejercicio 1
Vo = 0 a = 2 m/s t = 10 s Vf = ?
- Se plantea la fórmula mas útil
- vf = vo + a * t
- Al no tener que despejar se sustituyen directamente los datos
- vf = 0 + 2 * 10 s
- Se realizan las operaciones
- vf = 20
Ejercicio 2: Una persona que comienza caminando a una velocidad de 1 m/s comienza a acelerar y al cabo de 30 segundos la persona está corriendo a una velocidad de 5 m/s. ¿Cuál fue la distancia que recorrió esta persona?
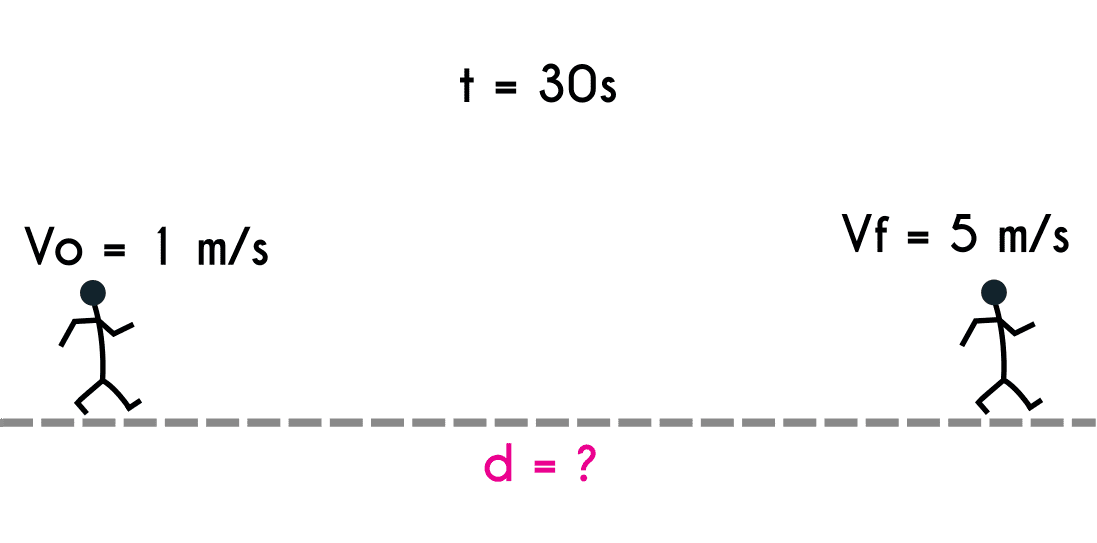
Datos del ejercicio 2
Vo = 1 m/s vf = 5 m/s t = 30 s d = ?
- Se plantea la fórmula
- d = vo + vf2* t
- Se reemplazan los datos
- d = 1 + 52* 30
- Se realizan las operaciones
- d = 62* 30
- d = 3 * 30
- d = 90
Ejercicio 3: Un vehículo que va a 33.2 m/s comienza a frenar y termina en estado de reposo, si se sabe que su aceleración fue de -2 m/s ¿Cuál fue la distancia que recorrió en total?.
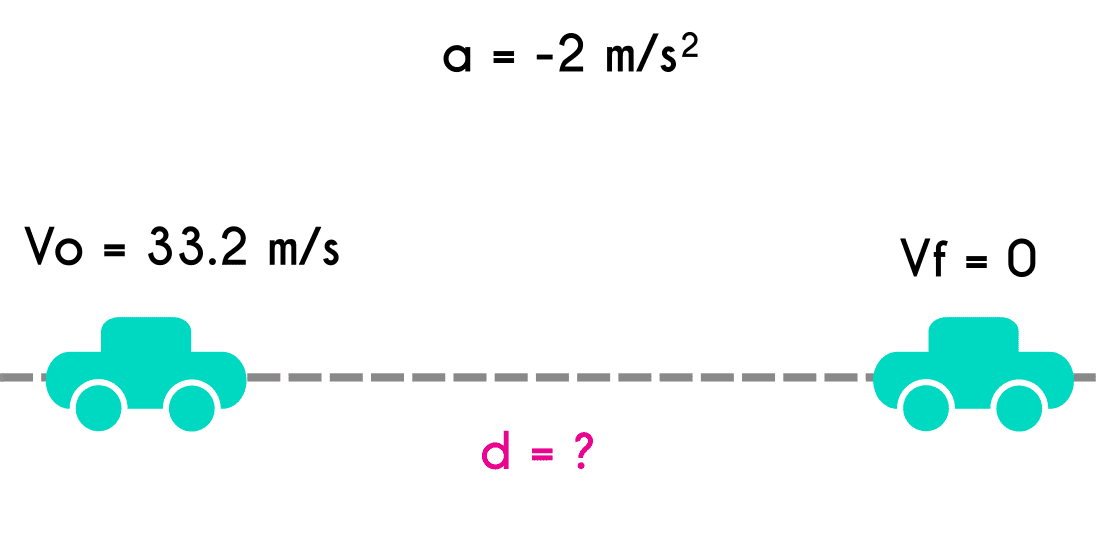
Datos del ejercicio 3
Vo = 33.2 m/s Vf = 0 m/s a = -2m/s d = ?
- Se plantea la fórmula usar
- vf2 = vo2 + 2a * d
- Se despeja la distancia
- d = vf2 - vo22a
- Se sustituyen los datos
- d = 0 - 33.222(-2)
- Se realizan las operaciones
- d = -33.22-4
- d = -1102.24-4
- d = 275.56
Ejercicio 4: Una avioneta va volando en linea recta a una velocidad de 12 m/s, esta acelera y llega a una velocidad de 20 m/s, si se sabe que en ese lapso recorrio una distancia de 300 metros, calcular el tiempo que demoró y cual fue la aceleración que hubo.
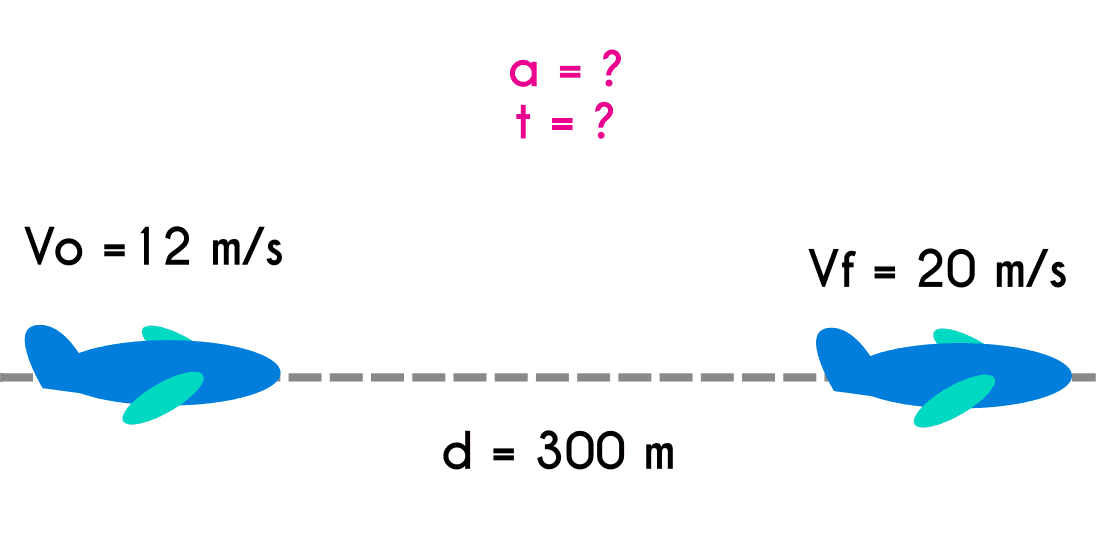
Datos del ejercicio 4
Vo = 12 m/s Vf = 20 m/s d = 300 t = ? a = ?
- Se plantea la fórmula 5 para encontrar el tiempo
- d = vo + vf2* t
- Se despeja el tiempo
- t = 2dvo + vf
- Se cambian los datos y se resuelve
- t = 2(300)12 + 20
- t = 60032
- t = 18.75 s
- Ahora teniendo el tiempo, se plantea la primer formula para calcular la aceleracion
- vf = vo + a * t
- Se despeja la aceleración
- a = vf - vot
- Se reemplazan los datos y se resuelve
- a = 20 - 1218.75
- a = 818.75
- a = 0.43
Ejercicio 5: A un objeto se le aplico una aceleración de 3 m/s durante 9 segundos, si se sabe que en ese periodo recorrió 103 metros ¿Cuál es la velocidad inicial y final del objeto?
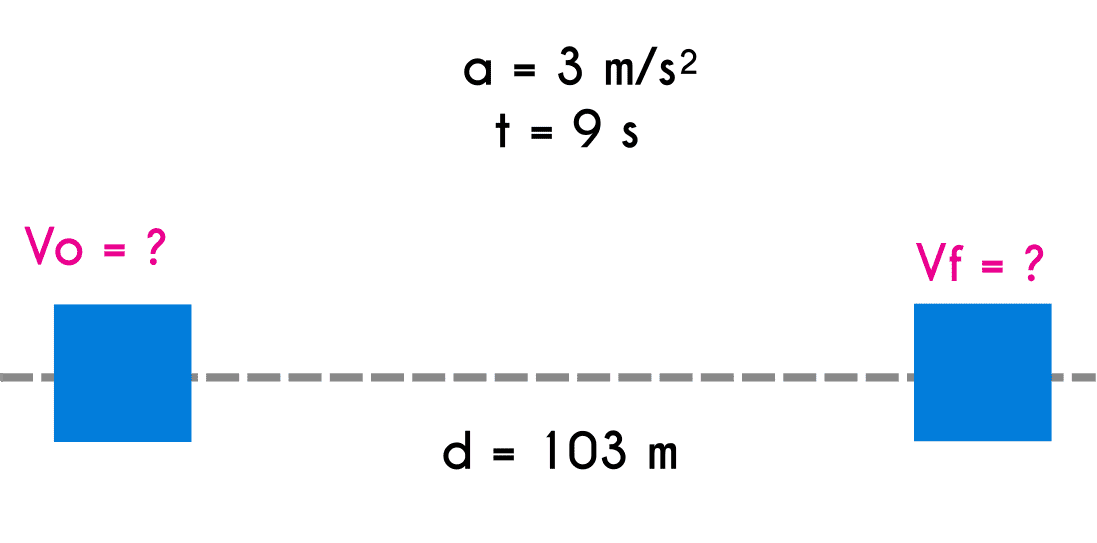
Datos del ejercicio 5
a = 3 m/s d = 103 m t = 9 s Vo = ? Vf = ?
- Se plantea la primer fórmula
- d = vo * t + 1/2a * t2
- Se despeja la velocidad inicial
- vo = d - 1/2a * t2t
- Se reemplazan los datos y se resuelve
- vo = 103 - 1/2(3) * (9)29
- vo = 103 - 1/2(3) * (81)9
- vo = 103 - 1/2(243)9
- vo = 103 - 121.59
- vo = -18.59
- vo = -2.06
- Se plantea la primer fórmula
- vf = vo + a * t
- Se reemplazan los datos y encuentra vf
- vf = -2.06 + 3 * 9
- vf = -2.06 + 27
- vf = 24.94
Ejercicio 6: En un parque de atracciones hay una montaña rusa donde los primeros 140 metros son en línea recta, si desde que el carrito esta en reposo hasta que llega a los 140 metros se le aplica una aceleración constante de 7.5 m/s, calcular el tiempo que toma en ese tramo y cuál es la velocidad final
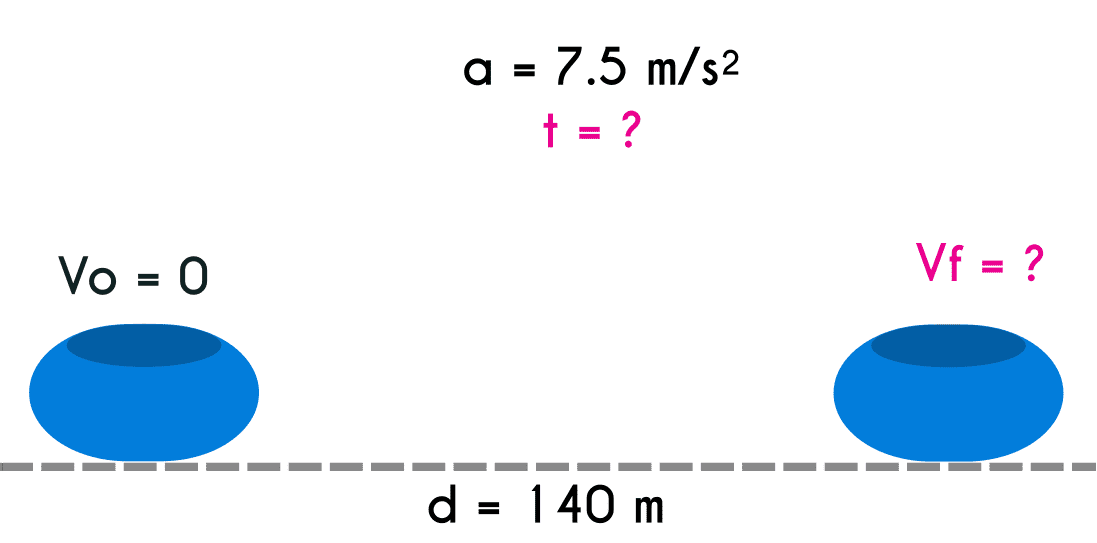
Datos del ejercicio 6
Vo = 0 m/s d = 140 m a = 7.5 m/s t = ? Vf = ?
- Se plantea la tercer ecuación
- vf2 = vo2 + 2a * d
- Se cambian los datos y se resuelve
- vf2 = vo2 + 2a * d
- vf2 = 0 + 2(7.5) * 140
- vf2 = 0 + 15 * 140
- vf = √ 2100
- vf = 45.82
- Ahora se encuentra el tiempo con la primer fórmula
- vf = vo + a * t
- Se despeja el tiempo
- t = vf - voa
- t = 45.82 - 07.5
- t = 6.11
Ejercicio 7: Un satélite en el espacio que se encuentra quieto, va modificar su posición moviéndose en línea recta, Si este logra tomar una velocidad de 3000 m/s en tan solo 0.9s ¿Cuál es la aceleración que se aplicó y la distancia recorrida en ese corto tiempo?
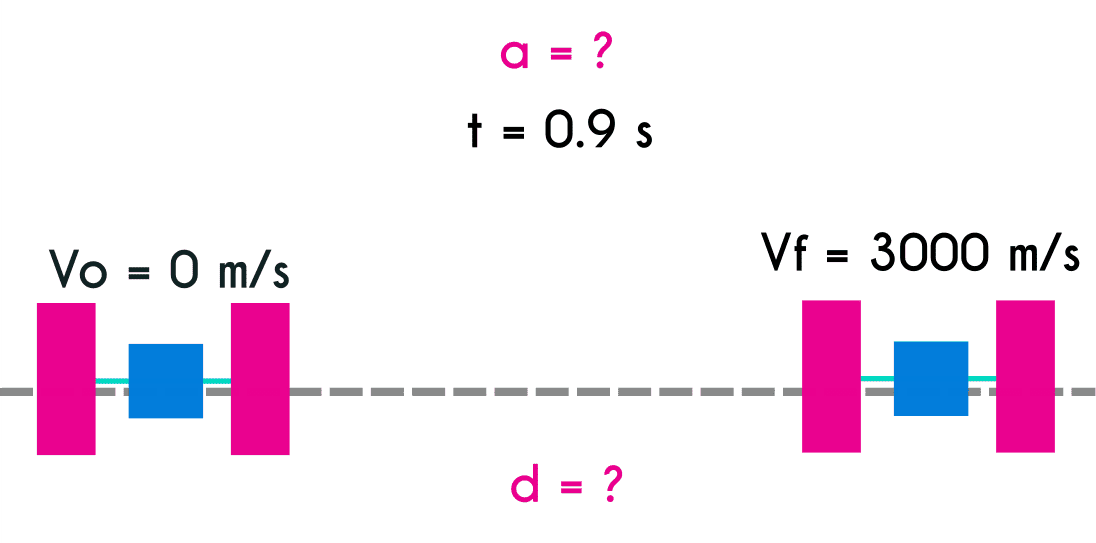
Datos del ejercicio 7
Vf = 3000 m/s Vo = 0 t = 0.9 s d = ? a = ?
- Primero se encontrará la distancia con la quinta fórmula
- d = vo + vf2* t
- d = 0 + 30002* 0.9
- d = 1500 * 0.9
- d = 1350
- Luego se calculará la aceleracion con la primer ecuación
- vf = vo + a * t
- Se despeja la aceleración
- a = vf - vot
- a = 30000.9
- a = 3333.33
Ejercicio 8: Una lancha que recorre un lago va a 5m/s, pero si este acelera a razón de 1m/s durante 40 metros ¿Cuál fue el tiempo que aceleró?
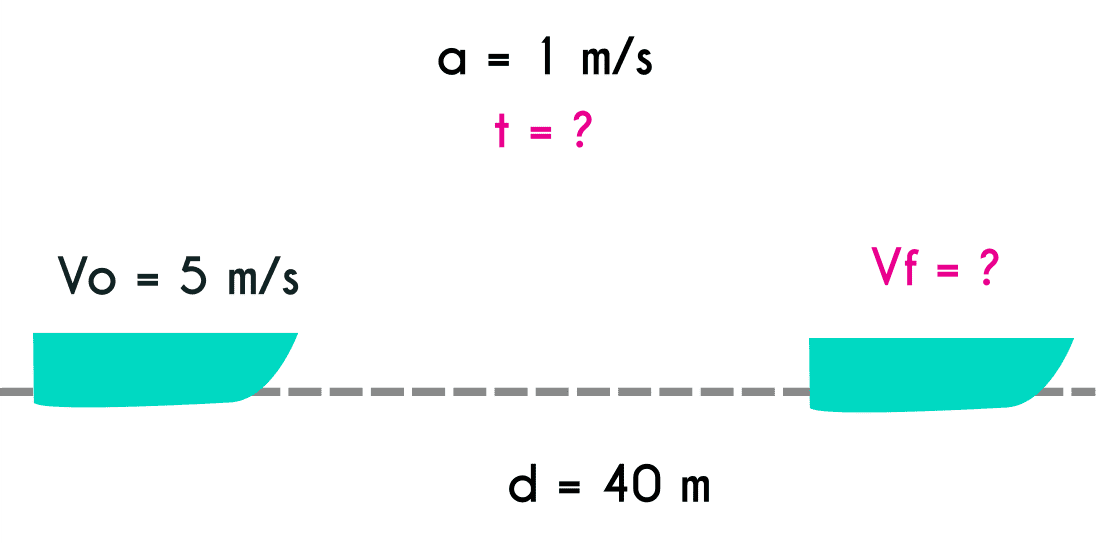
Datos del ejercicio 8
d = 40 m Vo = 5 m/s a = 1 m/s t = ?
Este ejercicio se puede resolver de varias maneras, porque si se busca en las formulas de mruv una con la que se pueda encontrar el tiempo teniendo la distancia, la velocidad inicial y la aceleración, solo hay una y es la segunda ecuación, pero despejar el tiempo en esta fórmula no es sencillo, por lo que la forma fácil de realizar este ejercicio es encontrar otro dato con las otras fórmulas, por ejemplo se podría utilizar la formula 3 para encontrar la velocidad final y luego utilizar la formula 1 o 5 para encontrar finalmente el tiempo, pero en esta ocasión se resolverá de la manera complicada y utilizando la fórmula 2.
En estos casos lo primero que se hace es ordenar la formula hasta que se tenga una ecuación de segundo grado y luego se factoriza la ecuación.
- Se plantea la ecuación 2
- d = vo * t + 1/2a * t2
- Ahora se reemplazan y hacen las operaciones que se puedan
- 40 = 5t + 0.5t2
- Luego se pasan todos los datos en el mismo lado y se ordenan
- 0.5t2 + 5t - 40 = 0
Ahora con esto se puede factorizar para encontrar el valor del tiempo, recordatorio: al factorizar una ecuación de segundo grado, el valor de la incógnita siempre dará dos resultados, pero al ser en este caso el tiempo, este no puede ser negativo, por lo que si en una de las respuestas da un tiempo menor a cero entonces se tomará como resultado la otra respuesta. Hay varias maneras de factorizar una ecuación de segundo grado, pero esto se vuelve muy complicado y en ocasiones imposible cuando en la ecuación hay decimales, por lo que se resolverá utilizando la famosa ecuación de segundo grado.
- a = 0.5, b = 5, c = -40
- t = -b ± √b2 - 4ac2a
- t = -5 ± √52 - 4(0.5)(-40)2(0.5)
- t = -5 ± √25 +801
- t = -5 ± √25 +80
- t = -5 ± √105
- t = -5 ± 10.25
- Solución para t1
- t = -5 + 10.25
- t = 5.25
- Solución para t2
- t = -5 - 10.25
- t = -15.25
- Como no puede haber tiempos negativos, la respuesta es t = 5.25
Aplicaciones del MRUV en Otros Tipos de Movimientos
El movimiento rectilíneo uniformemente variado (MRUV) no solo se limita a su aplicación directa, sino que también desempeña un papel fundamental en la descripción de otros movimientos estudiados en cinemática. Dos ejemplos destacados son el tiro vertical y la caída libre, que, aunque poseen características específicas, pueden considerarse como casos particulares de MRUV con parámetros particulares.
Artículos relacionados