Movimiento rectilíneo uniforme (mru)
En este artículo, exploraremos la definición del Movimiento Rectilíneo Uniforme (MRU) junto con las fórmulas que se utilizan para resolver ejercicios. Además, proporcionaremos ejemplos de movimientos que exhiben las características de un MRU.
Introducción al Movimiento Rectilíneo Uniforme (MRU)
El Movimiento Rectilíneo Uniforme, comúnmente conocido como MRU, es un concepto fundamental en la física que describe el movimiento de un objeto a lo largo de una trayectoria recta con una velocidad constante. En un MRU, la velocidad del objeto no varía, lo que significa que no experimenta ninguna aceleración. Este movimiento se encuentra en numerosos escenarios de la vida cotidiana y es crucial para comprender los principios básicos de la cinemática.
Características del MRU
Para comprender a fondo el MRU, es importante conocer sus características clave:
- Trayectoria en línea recta: En el MRU, el objeto se desplaza a lo largo de una línea recta sin desviaciones significativas. Esta característica permite simplificar los cálculos y análisis del movimiento.
- Velocidad constante: En un MRU, la velocidad del objeto permanece invariable a lo largo de su recorrido. Esto significa que no experimenta cambios en su rapidez ni en su dirección, lo que se traduce en una aceleración igual a cero.
El MRU se manifiesta en numerosas situaciones cotidianas, como el movimiento de un tren que viaja en línea recta a una velocidad constante, el desplazamiento de un automóvil en una carretera recta a una velocidad constante, o incluso el simple acto de caminar a una velocidad constante sin acelerar ni desacelerar.
Historia del MRU
El concepto de Movimiento Rectilíneo Uniforme (MRU) tiene sus raíces en la antigüedad. Los primeros indicios de la comprensión de este tipo de movimiento se remontan a los filósofos griegos, como Aristóteles, quien clasificó los movimientos en naturales y violentos, y reconoció que un objeto en movimiento uniforme continuaría en esa trayectoria a menos que se aplique una fuerza.
Sin embargo, la verdadera revolución en la comprensión del MRU se produjo durante la época de Galileo Galilei en el siglo XVII. Galileo realizó experimentos y formuló leyes que establecieron los fundamentos de la cinemática, incluyendo el principio del MRU. Su trabajo fue un avance significativo en la física y allanó el camino para futuros desarrollos en el campo de la mecánica.
Aplicaciones del Movimiento Rectilíneo Uniforme en la Vida Real
El MRU es un concepto fundamental en la física y encuentra una amplia gama de aplicaciones en la vida cotidiana y en diversas profesiones. Algunas de las aplicaciones más destacadas incluyen:
En la industria del transporte, el MRU se utiliza para modelar el movimiento de vehículos en carreteras rectas, ferrocarriles y sistemas de transporte público. Esto es esencial para garantizar la eficiencia y la seguridad en el transporte de personas y mercancías.
En la ingeniería de software y el desarrollo de videojuegos, el MRU se emplea para simular el movimiento de personajes y objetos en entornos virtuales, lo que permite crear experiencias de usuario más realistas.
En deportes y atletismo, el MRU se aplica al analizar el rendimiento de los atletas, especialmente en disciplinas como el atletismo y la natación. Ayuda a optimizar las técnicas de entrenamiento y a mejorar el rendimiento deportivo.
En la enseñanza de la física y la educación científica, el MRU es un componente esencial para comprender los conceptos básicos de la cinemática y sentar las bases para comprender movimientos más complejos y teorías más avanzadas.
Estos son solo algunos ejemplos de cómo el MRU es una herramienta fundamental en una variedad de campos, lo que subraya su relevancia en nuestra vida cotidiana y en la comprensión de los principios fundamentales de la cinemática.
Uso del MRU
El Movimiento Rectilíneo Uniforme (MRU) resulta ser una herramienta útil para calcular la velocidad promedio en situaciones en las que medir la velocidad de un objeto se vuelve complicado sin equipo especializado. Sin embargo, si conoces la distancia que ha recorrido un objeto (lo cual puedes medir fácilmente con una cinta métrica) y el tiempo que ha tomado para completar ese recorrido (lo cual puedes medir con un simple cronómetro o reloj), con el estudio del MRU es posible determinar la velocidad sin necesidad de instrumentos sofisticados.
Es importante señalar que la velocidad obtenida de esta manera es una "velocidad promedio". En la vida cotidiana, es raro encontrar situaciones de velocidad constante. Por ejemplo, si una persona camina 5 metros en 5 segundos, es poco probable que haya mantenido una velocidad constante durante todo el trayecto. Es decir, es muy probable que algunos pasos hayan sido más largos que otros, incluso si es solo por centímetros, lo que significa que la velocidad no es completamente constante. A pesar de esta variabilidad, el cálculo de la velocidad promedio mediante el MRU es bastante preciso.
Fórmulas del MRU
En problemas de Movimiento Rectilíneo Uniforme (MRU), siempre trabajamos con tres magnitudes físicas: el tiempo (que puede medirse en segundos, minutos o horas), la distancia (que puede medirse en metros, kilómetros o millas), y la velocidad (que se mide en metros por segundo o kilómetros por hora). La velocidad en un MRU es la relación entre el tiempo y la distancia. Por ejemplo, si un coche se mueve 10 metros por cada segundo que pasa, entonces su velocidad es de 10 metros por segundo.
Normalmente, en problemas de cinemática en general, las unidades de medición "estándar" son metros y segundos, pero los resultados no se ven afectados si las magnitudes físicas se miden en kilómetros y horas, millas y horas, etc., siempre y cuando todas las magnitudes físicas sean equivalentes. Sin embargo, en los ejemplos que se resolverán en este artículo, utilizaremos metros y segundos.
- Fórmulas del movimiento rectilíneo uniforme
- V = DT
- T = DV
- D = V * T
- ó
- X = Xo + V * T
Triángulo MRU
Una forma simple de recordar estas fórmulas es a través del triángulo MRU. Este triángulo es una herramienta mnemotécnica que funciona de la siguiente manera: para encontrar una variable, simplemente tapa o ignora esa variable en el triángulo, y lo que queda te proporciona la ecuación necesaria. Si dos variables están alineadas una al lado de la otra, se multiplican, y si están una sobre la otra, se dividen. Es importante recordar que la distancia siempre se coloca en la parte superior del triángulo.
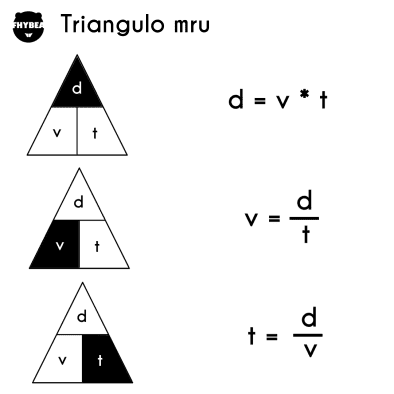
Gráficos de un MRU
Gráfico de posición-tiempo (p-t): En un MRU, el gráfico de posición-tiempo (p-t) representa la posición del objeto en función del tiempo. Este gráfico suele adoptar una forma lineal, con la pendiente de la línea reflejando la velocidad del objeto. La relación entre la pendiente y la velocidad es un aspecto clave de este tipo de gráfico.
Gráfico de velocidad-tiempo (v-t): En un MRU, el gráfico de velocidad-tiempo (v-t) es una representación constante, lo que significa que se presenta como una línea recta sin pendiente. Esta constancia de la velocidad en el tiempo se refleja claramente en el gráfico v-t, lo que lo convierte en una herramienta valiosa para comprender la velocidad constante en este tipo de movimiento.
Ejemplos MRU
Movimientos que poseen las caracteristicas de un movmiento rectilíneo uniforme.
- Un tren que viaja en línea recta a una velocidad constante
- Una lancha que avanza en línea recta
- Alguien en una cinta transportadora de personas
- Una persona caminando a un paso continuo
- Un avión que viaja a una velocidad fija
- Una maleta que pasa una revisión en el aeropuerto
- Cualquier objeto en una banda transportadora
- Una persona que corre cierta cantidad de kilómetros en un periodo de tiempo
Ejercicios resueltos
Ejercicio 1: Un vehículo viaja a una velocidad constante de 20 m/s ¿Cuantos metros avanzó el vehículo al cabo de 30 segundos?
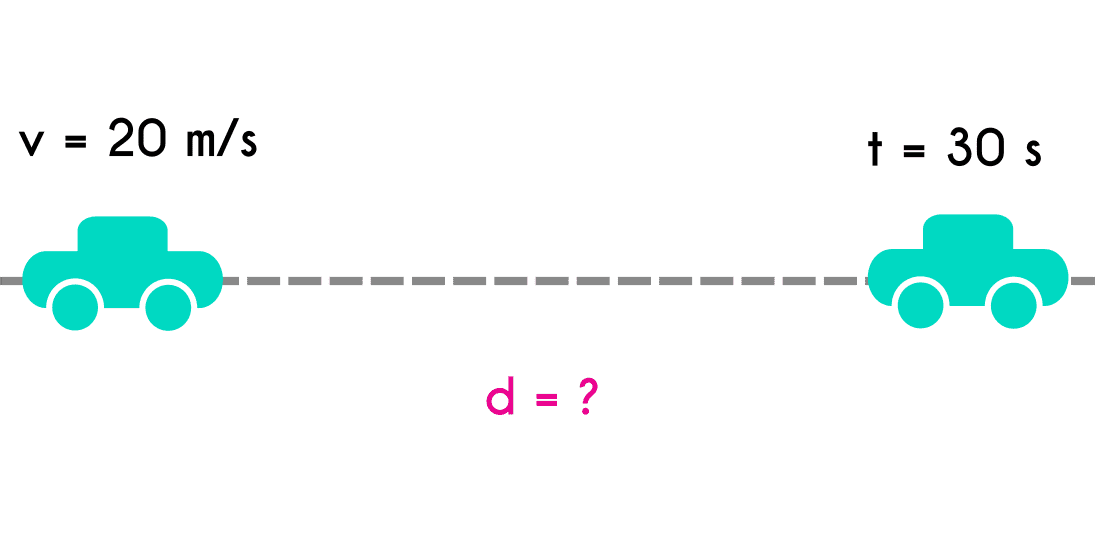
v = 20m/st = 30s d = ?
- Se plantea la ecuación
- D = v * t
- Se reemplazan las variables
- D = 20 m/s * 30 s
- Se realiza la operación
- D = 600 m
Ejercicio 2: Un tren avanzó 30 metros en un tiempo de 2.4 segundos, si la velocidad del tren era constante ¿Cuál fue la velocidad del tren durante los 2.4 segundos?
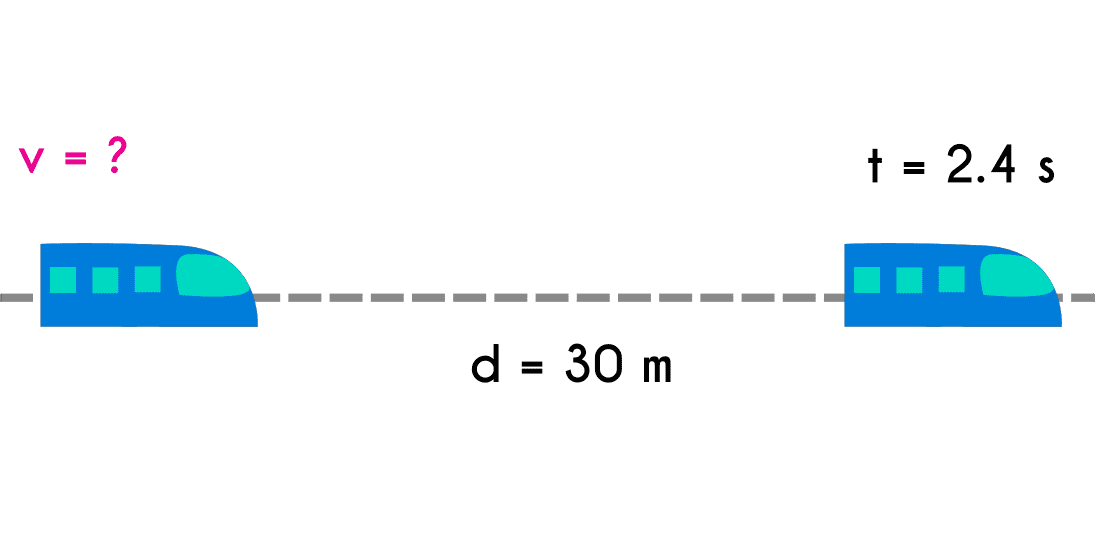
d = 30mt = 2.4s v = ?
- Se plantea la ecuación
- V = d / t
- Se reemplazan las variables
- D = 30 m / 2.4 s
- Se realiza la operación
- V = 12.5 m/s
Ejercicio 3: ¿Cuánto tiempo tardo un corredor olímpico en completar los 100 metros si empezó a una velocidad constante de 12.3 m/s.
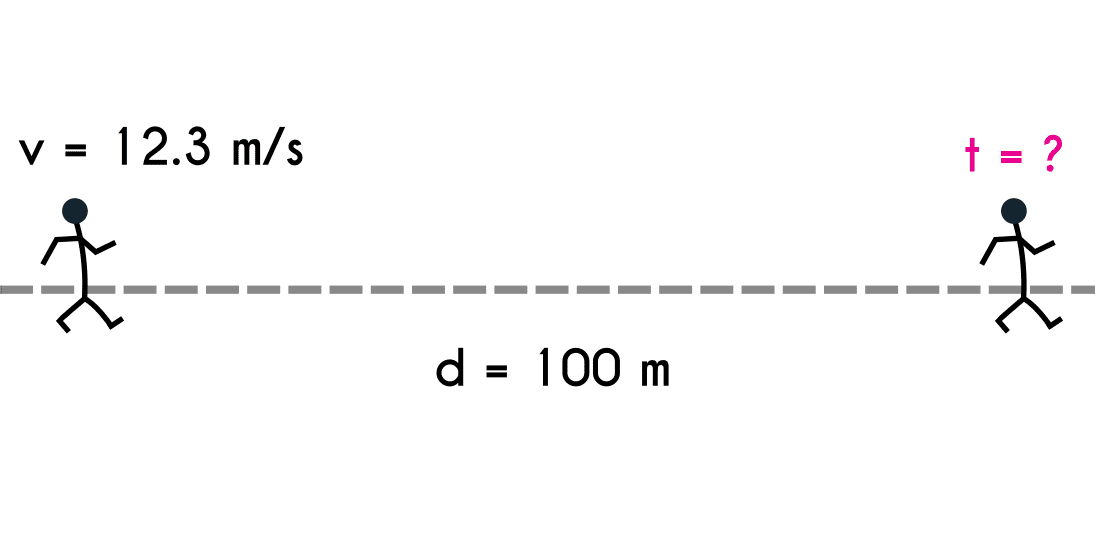
d = 100mv = 12.3m/s t = ?
- Se plantea la ecuación
- T = d / v
- Se reemplazan las variables
- T = 100 m / 12.3 m/s
- Se realiza la operación
- T = 8.13 s
Ejercicio 4: Una ballena tiene que emigrar 10 kilómetros hacia el este, si esta tiene que llegar a su destino en 24 horas, ¿a qué velocidad debe de nadar la ballena para llegar a tiempo?
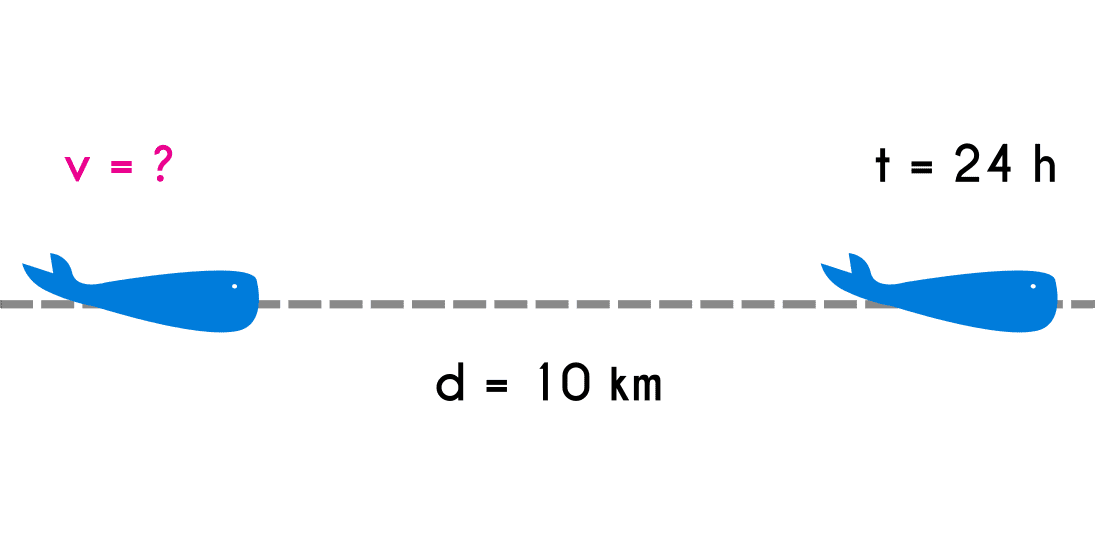
d = 10kmt = 24h v = ?
Ojo, Lo primero que se hará en este caso es convertir los kilómetros en metros y horas en segundos para trabajar con las unidades de medición estándar, aunque al ser kilómetros y horas se podría resolver sin convertir, pero en este caso se van a convertir de kilómetros y horas a metros y segundos.
- Se convierten los kilómetros en metros
- D = 10 km * 1000
- D = 10 000 m
- Se convierten las horas en segundos
- T = 24 h * 3 600
- T = 86 400
- Luego se plantea la ecuación
- V = d / t
- Se reemplazan las variables
- V = 10 000 m / 86 400s
- Se realiza la operación
- V = 0.12 m/s
Ejercicio 5: Hay dos hombres que practican caminata olímpica. El hombre a recorre una distancia de 37 metros en 12.5 segundos, mientras que el hombre b hace logra una distancia de 44 metros en 19.3 segundos, conociendo esto: ¿Cuál de los dos hombres fue más rápido?
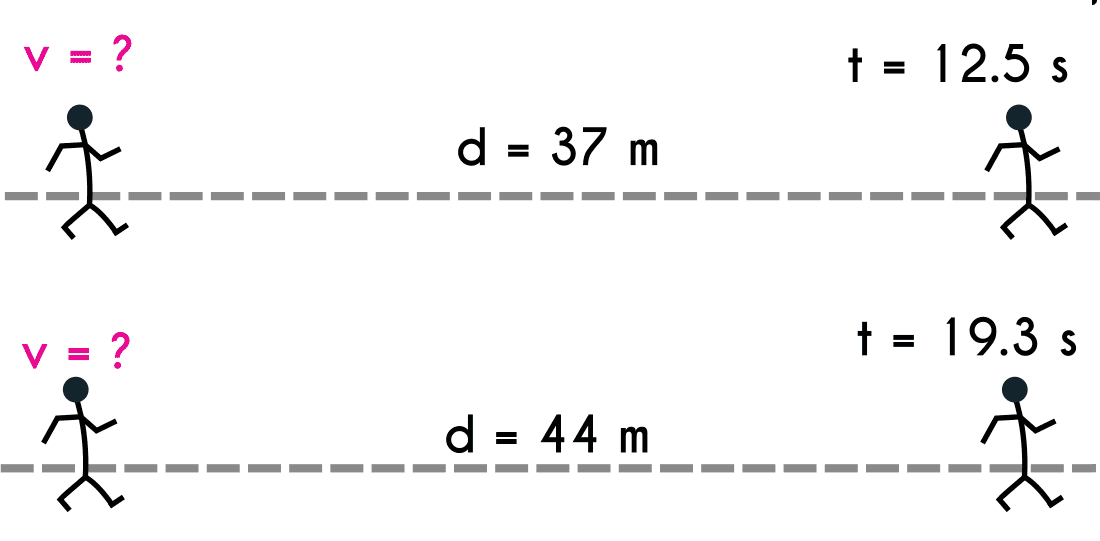
Hombre a: d = 37mt = 12.5s v = ?
- Hombre a
- V = d / t
- V = 37m / 12.5s
- V = 2.96 m/s
Hombre b: d = 44mt = 19.3s v = ?
- Hombre b
- V = d / t
- V = 44m / 19.3s
- V = 2.28 m/s
Como conclusión, el hombre a es más rápido que el hombre b.
Ejercicio 6: Dos vehículos hacen diferentes recorridos, el primer conche recorre una distancia de 400 metros a una velocidad de 10 m/s, mientras que el segundo vehículo recorre 700 metros a una velocidad de 16.3 m/s ¿Cuál de los dos coches realizó su recorrido en menor tiempo?
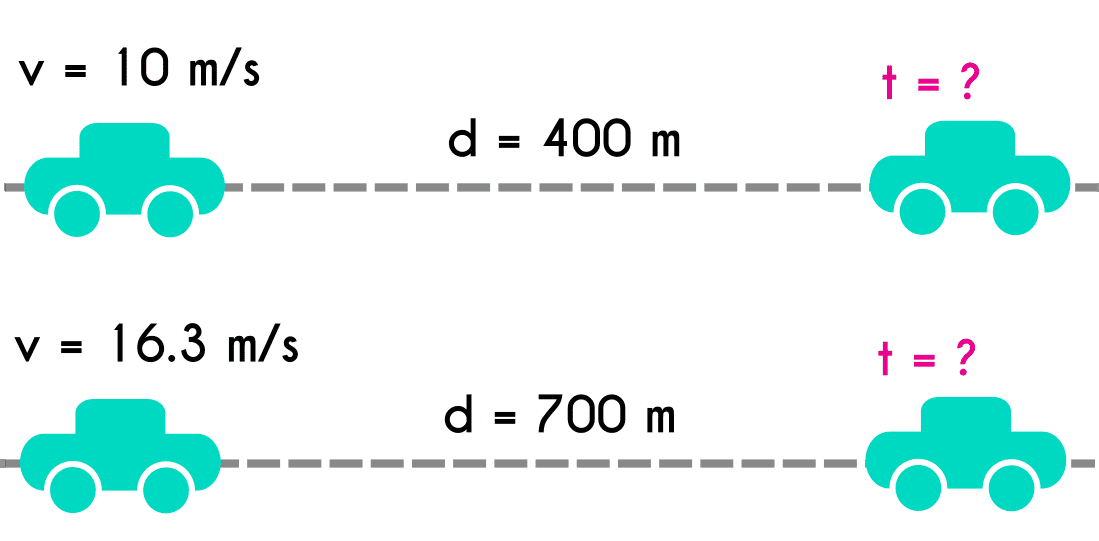
Coche 1: v = 10 m/sd = 400 m t = ?
- Coche 1
- t = d / v
- t = 400 / 10s
- t = 40 s
Coche 2: v = 16.3 m/sd = 700 m t = ?
- Coche 2
- t = d / v
- t = 700 / 16.3
- t = 42.94
Ejercicio 7: Una persona se prepara para una Maratón, corriendo durante una hora a una velocidad de 3 m/s todos los días. ¿Cuál es la distancia que recorre esta persona luego de 10 días?
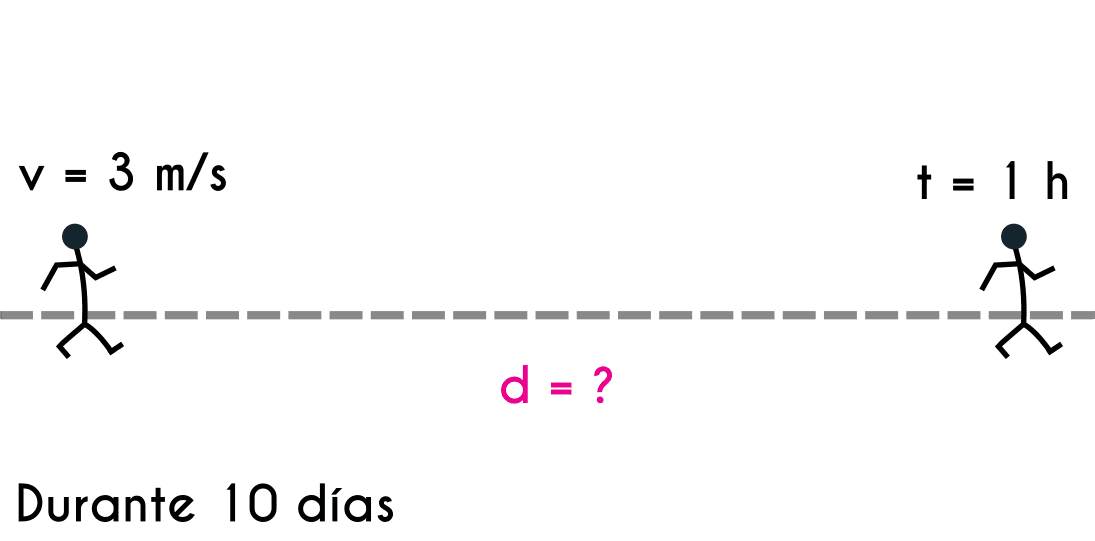
v = 3 m/st = 1 h durante 10 días d = ?
- Primero se convierten las horas en segundos
- t(segundos)= 1h * 60 * 60
- t = 3600 segundos
- Ahora se encuentra la distancia que recorre en una hora
- d = v * t
- d = 3 * 3600
- d = 10 800
- Luego se multiplica por 10 días
- d(10 días) = 10 800 * 10
- d(10 días) = 108 000 metros
Ejercicio 8: Un tren viaja en una velocidad de 20 metros por segundo sobre unas vías que son en línea recta, calcular la distancia recorrida luego de 10, 25 y 60 minutos.
v = 20 m/st = 10min, 25min, y 60 min d = ?
- Distancia luego de 10 minutos
- t(segundos)= 10 min * 60 segundos
- t = 600s
- d = v * t
- d = 20 * 600
- d = 12 000 metros
- Distancia luego de 25 minutos
- t(segundos)= 25 min * 60 segundos
- t = 1 500s
- d = v * t
- d = 20 * 1 500
- d = 30 000 metros
- Distancia luego de 60 minutos
- t(segundos)= 60 min * 60 segundos
- t = 3 600s
- d = v * t
- d = 20 * 3 600
- d = 72 000 metros
Conclusiones sobre el MRU
El Movimiento Rectilíneo Uniforme (MRU) es un concepto fundamental en la física que describe un tipo específico de movimiento en el cual un objeto se desplaza en línea recta a una velocidad constante. A lo largo de este artículo, hemos explorado las características principales del MRU, desde su definición hasta sus aplicaciones en la vida cotidiana y diversas profesiones.
El MRU es esencial para entender los principios fundamentales de la cinemática y proporciona una base sólida para abordar movimientos más complejos. Además, hemos analizado las fórmulas, gráficos y el "triángulo MRU" que facilitan la resolución de problemas relacionados con este tipo de movimiento.
En resumen, el MRU, con su simplicidad y utilidad, es un pilar fundamental en la física y tiene un impacto significativo en una variedad de campos, desde la ingeniería y la informática hasta el deporte y la educación. Comprender el MRU es un paso crucial para adentrarse en el fascinante mundo de la cinemática y la mecánica clásica.
Artículos relacionados