Movimiento circular uniformemente acelerado (MCUA)

En este artículo Se definirán las características principales de un MCUA (también conocido como MCUV), su definición, ejemplos y ejercicios resueltos con la fórmulas de este movimiento.

Definicion MCUA

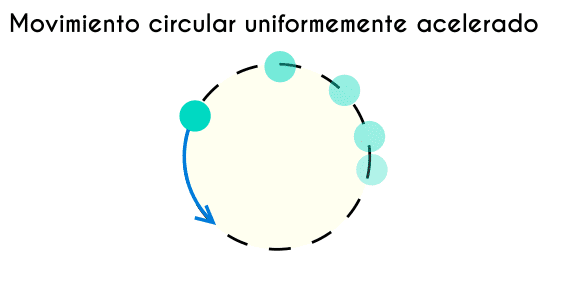
El movimiento circular uniformemente acelerado (mcua) o también conocido como movimiento circular uniformemente variado (mcuv) es un movimiento que se caracteriza por tener una trayectoria que describe un circulo cuya velocidad angular y velocidad tangencial del objeto aumentan o disminuyen (dependiendo de la dirección o signo de las aceleraciones correspondientes.) constantemente. En el movimiento circular uniformemente acelerado afectan 3 aceleraciones diferentes: aceleración angular, aceleración tangencial y aceleración centrípeta, y en el vector velocidad del objeto varian todos los componentes, es decir, varia el modulo o magnitud, la dirección y el sentido.

Como se describe en el párrafo anterior, en mcua intervienen varias velocidades y aceleraciones, por eso hay que tener muy claro el concepto tanto de velocidad y aceleración: la velocidad de un objeto define cuanto avanza un cuerpo en un periodo de tiempo, y una aceleración es un valor que condiciona el cambio de la velocidad, por ejemplo si la aceleración de un objeto es de 1m/s esto quiere decir que la velocidad de será 1m/s mas alta por cada segundo que pasa, lo que complica este concepto es que en un movimiento circular intervienen aceleraciones que no cambian solo el valor de la velocidad sino también la dirección de esta y esto es lo que provoca que un objeto se mueva en círculos una y otra ves.

Velocidades y Aceleraciones en un movimiento circular uniformemente acelerado

El mcua se divide en dos partes, la parte angular y la parte tangencial. La parte angular del problema trata de la rotación u orbita de un cuerpo, a que velocidad rota un objeto sobre su centro y que aceleración angular se aplica sobre un objeto, cuando se está en esta parte de los problemas, las medidas de longitud no importan, solamente se toman en cuenta las magnitudes de inclinación, mientras que la parte tangencial de un mcua se encarga únicamente de longitudes, por ejemplo cuanta distancia avanzó un objeto, la velocidad que un objeto lleva o la aceleración que se está ejerciendo sobre un cuerpo. Aunque ambas partes por lo general se trabajan por separado, existen ecuaciones que permiten conectar estas dos partes, y de esta manera se puede resolver un problema por completo aunque solamente se tengan datos de una de las partes.

aceleración angular (α): es la que aumenta o disminuye la magnitud de la velocidad angular, esta aceleración es constante y se expresa en rad/s2

Velocidad angular (ω): esta velocidad define la cantidad de radianes que un cuerpo rota en cierta cantidad de tiempo, en ejemplos de mcua siempre va a haber una velocidad angular inicial y final, se representa por el símbolo ω y se expresa en rad/s

Aceleración tangencial (A_t): esta aceleración es lo mas parecida a la aceleración en movimientos rectilíneos, pues esta aumenta o disminuye la velocidad a la que un objeto se mueve y se representa en m/s2

Velocidad tangencial (V_t): Es la longitud que avanza un cuerpo en un periodo de tiempo, esta velocidad varia tanto en su magnitud como en su dirección constantemente. Al igual que la velocidad angular, la velocidad tangencial en un mcua siempre va a tener una velocidad inicial y una velocidad final, y estas se representan por la letra V_t y son expresadas en m/s

Aceleración centrípeta (A_c): Esta aceleración es la que varía la dirección de la velocidad de un objeto en movimiento circular uniforme, y se puede encontrar utilizando cualquiera de las dos aceleraciones anteriores.

Como se explica anteriormente, la parte angular y tangencial se trabajan de manera separada, pero las ecuaciones que se ocupan son prácticamente iguales en ambas partes, solamente se cambian las variables, y estas son las mismas que se utilizan en un mruv.

S = distancia que recorre un cuerpo en la circunferencia (metros)

En un movimiento circular uniformemente variado, toda magnitud tangencial se puede encontrar en base a la misma magnitud angular con solo multiplicarla por el radio de circulo, por ejemplo, la velocidad tangencial se puede calcular multiplicando la velocidad angular por el radio.

1. Las hélices de un helicóptero cuando se inicia el motor
2. Las aspas de un ventilador cuando se prende
3. Las ruedas de un vehículo cuando acelera constantemente
4. Cuando se inicia el lector de un disco
5. Un tocadisco que gira hasta alcanzar la velocidad de rotacion necesaria

Artículos relacionados

Otros temas