Movimiento circular uniforme (mcu)
Este artículo se centra en explorar el concepto del Movimiento Circular Uniforme (MCU) y abarca todos los elementos esenciales para comprender su comportamiento. Proporcionaremos una completa colección de fórmulas para la resolución de problemas, ejemplos ilustrativos y ejercicios prácticos que te ayudarán a profundizar en este tema.
Definición de Movimiento Circular Uniforme
El Movimiento Circular Uniforme (MCU), a menudo abreviado como MCU, es un tipo de movimiento en el cual un objeto se desplaza a lo largo de una trayectoria circular. Lo característico de este movimiento es que la velocidad del objeto cambia de dirección constantemente.
Es importante destacar que la velocidad es una magnitud vectorial, lo que significa que tiene dirección, magnitud y sentido. En un MCU, la magnitud del vector velocidad se mantiene constante, pero su dirección cambia de forma continua. Por lo tanto, aunque la magnitud de la velocidad permanece invariable, no se puede afirmar que la velocidad en un MCU sea constante.
En un movimiento circular uniforme, intervienen dos componentes principales: las velocidades y la aceleración. La aceleración en este contexto se llama aceleración centrípeta, y es la responsable de cambiar la dirección de la velocidad de un objeto en MCU.
Aunque en este movimiento intervienen varias magnitudes físicas, en parte es similar a un Movimiento Rectilíneo Uniforme (MRU). De hecho, en problemas de MCU que solo incluyen velocidad angular, ángulo y tiempo, las fórmulas son idénticas a las del MRU, solo que se cambian los nombres de las variables.
El Movimiento Circular Uniforme se encuentra presente en la gran mayoría de mecanismos, ya que la rotación de partes y objetos es la base principal de los motores y de muchos componentes en diversos aparatos. Además, este movimiento también se manifiesta en el desplazamiento de partículas.
Conceptos Clave en el Movimiento Circular Uniforme (MCU)
En el Movimiento Circular Uniforme (MCU), intervienen diversas magnitudes que desempeñan un papel crucial en su estudio. Estas magnitudes incluyen velocidades, aceleraciones y ángulos, y al resolver problemas relacionados con el MCU, es necesario comprender cada una de ellas, cómo funcionan y cómo afectan al movimiento.
Aceleración Centrípeta
La aceleración centrípeta es una aceleración que no altera la magnitud de la velocidad de un objeto en MCU, pero provoca un cambio constante en la dirección de esa velocidad. Es esta aceleración la que da lugar a la trayectoria circular del objeto.
Velocidad Angular
La velocidad angular se refiere a la velocidad a la que un objeto rota alrededor de un centro. Esta velocidad se expresa como la relación entre los ángulos o radianes que el objeto recorre en un período de tiempo dado. Por ejemplo, si un objeto completa una vuelta en un círculo en una hora, su velocidad angular es de 360 grados por hora (360°/h). Las unidades de medida estándar para la velocidad angular son los radianes por segundo (rad/s) y los segundos. En este artículo, utilizaremos principalmente radianes por segundo.
Velocidad Tangencial
La velocidad tangencial se refiere a la relación entre la distancia que un objeto recorre en un cierto período de tiempo. Este concepto es más comúnmente utilizado en movimientos rectilíneos, y puede expresarse en diversas unidades, como millas por hora (mph) o kilómetros por hora (km/h). Sin embargo, en problemas relacionados con el MCU, se emplea con mayor frecuencia la unidad de metros por segundo (m/s).
Período
El período, representado por la letra mayúscula T, es el tiempo que un objeto en MCU necesita para completar una vuelta o ciclo completo en su trayectoria circular. Imagina un objeto que gira en círculos a una velocidad constante. El período nos dice cuánto tiempo le lleva al objeto dar una vuelta completa alrededor de su trayectoria. El período se mide en segundos (s), ya que es una unidad de tiempo.
Frecuencia
La frecuencia, representada por la letra "f", es la cantidad de vueltas o ciclos que un objeto realiza en un período de tiempo específico. Usualmente, este período de tiempo es de un segundo (s). En otras palabras, la frecuencia indica cuántas veces el objeto completa una vuelta en un segundo. La unidad de medida estándar para la frecuencia es el Hertz (Hz), que equivale a una vuelta por segundo.
Relación entre Período y Frecuencia
Es esencial comprender que el período y la frecuencia están relacionados de manera inversa. Esto significa que, al multiplicar el período (T) por la frecuencia (f), el resultado siempre será igual a uno: T * f = 1. Esto tiene sentido porque, si un objeto completa una vuelta en un período determinado, la frecuencia representa cuántas vueltas realiza en un segundo. Si el período es más largo, la frecuencia será menor y viceversa.
Aplicaciones Técnicas y Científicas del Movimiento Circular Uniforme
El Movimiento Circular Uniforme (MCU) es un concepto fundamental en la física y la ingeniería que tiene una amplia gama de aplicaciones tanto en el mundo técnico como en el científico. A continuación, se presentan algunas de las áreas en las que el MCU desempeña un papel crucial:
1. Ingeniería Mecánica
En la ingeniería mecánica, el MCU es esencial en el diseño y funcionamiento de una variedad de máquinas y dispositivos, como motores, turbinas y engranajes. La comprensión del MCU permite optimizar la eficiencia y la seguridad de estos sistemas.
2. Tecnología Aeroespacial
En la tecnología aeroespacial, el MCU se aplica en la trayectoria de vuelo de satélites, cohetes y naves espaciales. El control de la orientación y la navegación se basa en el conocimiento preciso de la velocidad angular y la aceleración centrípeta.
3. Física de Partículas
En la física de partículas, los aceleradores de partículas como el Gran Colisionador de Hadrones (LHC) utilizan el MCU para mantener partículas subatómicas en movimiento circular a velocidades cercanas a la velocidad de la luz. Esto permite estudiar las propiedades de las partículas y las interacciones fundamentales.
4. Tecnología de Imagen Médica
En la tecnología de imagen médica, los escáneres de resonancia magnética (MRI) utilizan campos magnéticos y gradientes de campo para generar imágenes detalladas del interior del cuerpo. Estos gradientes de campo aplican fuerzas que producen el MCU en los núcleos atómicos, lo que permite la obtención de imágenes de alta resolución.
5. Computación Gráfica y Animación
En la industria del entretenimiento, el MCU se utiliza en la creación de efectos especiales y animaciones computarizadas. Los motores de física utilizan el concepto de MCU para simular el movimiento de objetos en mundos virtuales de manera realista.
Estos son solo algunos ejemplos de las numerosas aplicaciones del MCU en la ciencia y la tecnología. Su comprensión y aplicación son fundamentales para avanzar en diversas disciplinas y mejorar la vida cotidiana.
Fórmulas del Movimiento Circular Uniforme
En el Movimiento Circular Uniforme (MCU), se pueden identificar dos aspectos distintos: el aspecto angular y el aspecto tangencial. El aspecto angular se relaciona con conceptos que involucran ángulos, como rotación e inclinación, mientras que el aspecto tangencial se refiere a magnitudes como el desplazamiento y las velocidades expresadas en km/h o m/s. Estos dos aspectos del MCU pueden ser analizados de manera independiente, aunque siempre están interconectados, y para pasar de uno al otro, se requiere conocer el radio del círculo en cuestión.
Existen varias fórmulas que se utilizan en el Movimiento Circular Uniforme, por lo que es fundamental comprender cuál aplicar en diferentes situaciones. Para facilitar esto, es esencial tener un entendimiento claro de los conceptos explicados anteriormente.
- Ecuaciones básicas
- Θ = ω * t
- ω = Θ / t
- t = Θ / ω
- Ecuaciones de frecuencia y periodo
- T = tiempovueltas
- T = 1f
- f = vueltastiempo
- f = 1T
- Ecuaciones velocidad tangencial (Vt)
- Vt = 2 * π RT
- Vt = 2 * π * R * f
- Ecuaciones velocidad angular (ω)
- ω = 2 * π T
- ω = 2 * π * f
- Ecuaciones aceleración centrípeta
- Ac = Vt2R
- Ac = ω2 * R
- Convertir de velocidad angular a velocidad tangencial
- ω = VtR
- Vt = ω * R
Ejemplos del movimiento circular uniforme
A continuación una lista de movimientos que se pueden apreciar a diario en los que se pueden observar un movimiento circular uniforme
- El movimiento de una noria (rueda de feria)
- La rotación constante de un neumático de un coche que va a una velocidad constante
- Las manecillas de un reloj
- El movimiento constante de las aspas de un ventilador
- La rotación de un molino de agua
Ejercicios del movimiento circular uniforme
Ejercicio 1: Un caballo en el carrusel de una feria tarda 25 segundos en dar una vuelta, si se sabe que desde el centro del carrusel hasta el caballo (el radio) hay una distancia de 2 metros, ¿Cuál es la velocidad tangencial a la que se mueve el caballo?
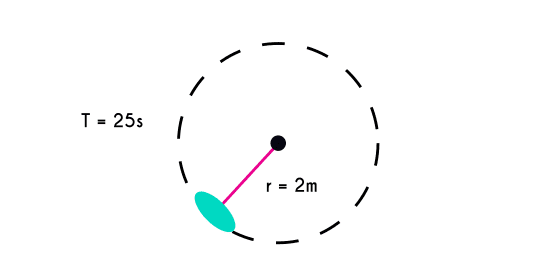
En este ejemplo se tienen dos datos, uno es el periodo T = 25s y el radio R=2, asi que se utilizará la fórmula de la velocidad tangencial con el periodo, en este caso las unidades ya están en metros y segundos por lo que no es necesario convertirlas.
- Vt = 2 * π * RT
- Vt = 2 * 3.1416 * 225
- Vt = 12.5725
- Vt = 0.502 m/s
Ejercicio 2: Cuál es la velocidad angular de las aspas de un ventilador si se sabe que el ventilador da un total de 200 vueltas por cada minuto
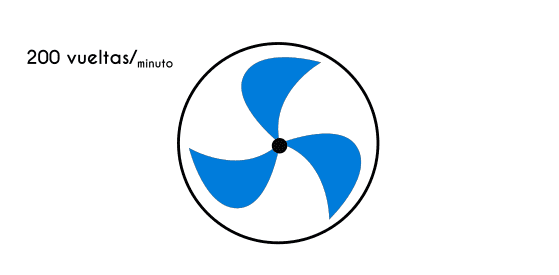
En este caso no se tiene ningún dato que se pueda utilizar directamente en las ecuaciones, pero con los datos que da el problema se puede encontrar ya sea el periodo o la frecuencia y con esto se puede calcular la velocidad angular.
- Primero se deben convertir los minutos en segundos
- tiempo = 1min
- tiempo (segundos) = 1min * 60 segundos
- tiempo (segundos) = 60 segundos
- Ahora se calcula la frecuencia
- f = vueltastiempo
- f = 20060
- f = 3.33 hz
Ahora conociendo la frecuencia se puede calcular la velocidad angular
- Ecuación de velocidad angular
- ω = 2 * π * f
- ω = 2 * 3.1416 * 3.33
- ω = 20.92 rad/s
Ejercicio 3: Calcular la aceleración centrípeta que tiene la punta de una manecilla que marca los segundos de un reloj, teniendo en cuenta que el tamaño de la manecilla es de 7 centímetros.

En este ejemplo se tienen dos datos, uno es el radio del circulo, porque la manecilla de los segundos mide 7 centímetros y como esta va desde el centro hasta la punta de la manecilla, entonces los 7 centímetros es el radio del circulo, otra cosa que se sabe es que da una vuelta cada 60 segundos, por lo que también se conoce el periodo.
- Se convierten los centímetros en metros
- R (metros) = 7cm / 100 cm/metros
- R (metros) = 0.07m
- T = 60s
Ahora se encontrará la velocidad angular para poder calcular luego la aceleración centrípeta
- se define la velocidad angular
- ω = 2 * πT
- ω = 2 * 3.141660
- ω = 6.2860
- ω = 0.105 rad/s
Y por último se calcula la aceleración centrípeta.
- Se encuentra aceleración centrípeta
- Ac = ω2R
- Ac = 0.10520.07m
- Ac = 0.0110.07m
- Ac = 0.157
Conclusión
El Movimiento Circular Uniforme (MCU) es un concepto fundamental en la física que desempeña un papel esencial en numerosas aplicaciones técnicas y científicas. A lo largo de este artículo, hemos explorado los conceptos básicos del MCU, incluyendo la aceleración centrípeta, la velocidad angular y la velocidad tangencial.
Hemos aprendido cómo el MCU se diferencia de otros tipos de movimiento, cómo se aplican las fórmulas correspondientes y cómo estas se utilizan para resolver problemas del mundo real. Además, hemos explorado las aplicaciones del MCU en campos tan variados como la ingeniería mecánica, la tecnología aeroespacial, la física de partículas, la medicina y la animación por computadora.
El MCU no solo es un concepto teórico, sino también una herramienta poderosa en la resolución de problemas prácticos y en la comprensión de fenómenos naturales y tecnológicos. Su capacidad para describir el movimiento en una trayectoria circular constante lo convierte en un pilar en la física y la ingeniería moderna.
En resumen, el MCU es un tema fascinante que combina conceptos matemáticos y físicos para explicar cómo objetos se mueven en círculos con velocidad constante. Su aplicabilidad en diversas disciplinas lo convierte en un tema de estudio valioso que sigue siendo relevante en la ciencia y la tecnología contemporáneas.
Artículos relacionados