The projectile motion with examples

This article will be about the projectile motion, the basic concepts, formulas, and examples.

Definition of the projectile motion

The projectile motion is a motion that is mainly characterized because it has a parabolic trajectory, this means that the object goes up and then it goes down, this meanwhile it advances in a straight line. This motion happens when we throw an object with a certain inclination degree, from the floor or from a platform, the object that will be thrown will move in two dimension, in the “x” and “y” axis.

(Representation of the projectile motion)

Composition of the projectile motion

As we said before, the projectile motion is a two dimensional motion, the union of this two dimensions is the product of the projectile motion, we can call this motion a compose motion, but the motion in both dimension is independent, the motion in the “x” axis is not the same motion as the motion in the “y” axis, this is why when we solve projectile motion problems we separate the motions, because it makes the work easier.

”X” axis motion: is a constant velocity motion, which means that the velocity in this axis will be always the same, and the gravity factor is not something to take into account.

”Y” axis motion: the motion in this axis is a uniformly accelerated motion, but with a little change, and is that the acceleration in this case will be the value of the gravity, and it will be the only acceleration affecting the object.

Projectile motion formulas

The formulas used in the resolution of projectile motion problems are the same as the constant velocity motion and the uniformly accelerated motion formulas, something that is important to know is that in most of the projectile motion problems we are going to have a general velocity, so we have to learn how to decompose the velocity.

Formulas for the x axis
t = x / v_x
v_x = x / t
x = v_x * t
Formulas for the y axis
v_y = vo_y - g * t
y = vo_y * t - 1/2g * t²
v_y² = vo_y² - 2g * y
y =
vo_y + v_y/2
* t

The formulas that are used in the “y” axis are the uniformly accelerated motion formulas, with the bit difference that the acceleration is the gravity, so instead of writing an “a” we are going to write a “g” making reference to gravity, but we also have to change the sign of the gravity because as we know, down and left directions are always taken as negative, and like the gravity is an acceleration that points down, the sign of the gravity will be negative.

The velocity of an object that is moving in 2 or more dimensions is the result of the union of the velocity in each dimension, in this case, the velocity is the union of the “x” and “y” velocity, so we have to learn how to decompose the velocity in this two axis, because we are going to work with this axis separately.

Like a velocity is a vector magnitude, this has direction, and magnitude, so it important to know the inclination degree of the velocity when the object is thrown.

Velocity vector
v_x = v * cos(Θ)
v_y = v * sen(Θ)
v = √v _x² + v _y²

Projectile motion examples

Example 1: An object is thrown from the floor at a velocity of 30 m/s with an inclination of 40 degrees, calculate the maximum height of the object and the total distance that it covered.

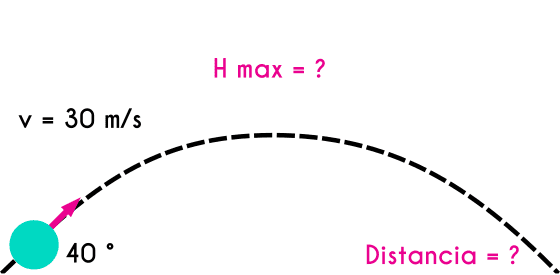
v = 30 m/s Θ = 40° Max height = ? Distance = ?

First we are going to calculate the maximum height, knowing that at a projectile motion the maximum height when the velocity in the y axis is equals to 0.

First we find the velocity on y
v_y = v * sen(Θ)
v_y = 30 * sen(40)
v_y = 19.28
Now we write the formula
v_y² = v_oy² - 2g * y
In this fomrula the variable "y" is the max height if the velocity is equals to 0
We clear "y" (max height)
Hmax =
v_y² - v_oy²/-2g
Hmax =
0² - 19.28²/-2(9.8)
Hmax =
-371/-19.6
Hmax = 18.96

Then we are going to calculate the range, for this we have to calculate the time in the x axis knowing that the object will impact with the same velocity as its initial velocity but in opposite direction (negative).

We write the formula and clear the time
v_y = vo_y - g * t
t max =
v_y - vo_y/-g
t max =
-19.28 - (19.28)/-9.8
t max =
-38.56/-9.8
t max = 3.93s

And now having this we can find the range in the x axis.

First we find the velocity on x
v_x = v * cos(Θ)
v_x = 30 * cos(40)
v_x = 22.98
and then we find the distance or range
d = v_x * t
d = 22.98 * 3.93
d = 90.31s

Example 2: A golf player hits the ball and it reaches a maximum height of 30 meters and it has a range of 90 meters, knowing this define the time of flight of the ball and the initial velocity of the ball.

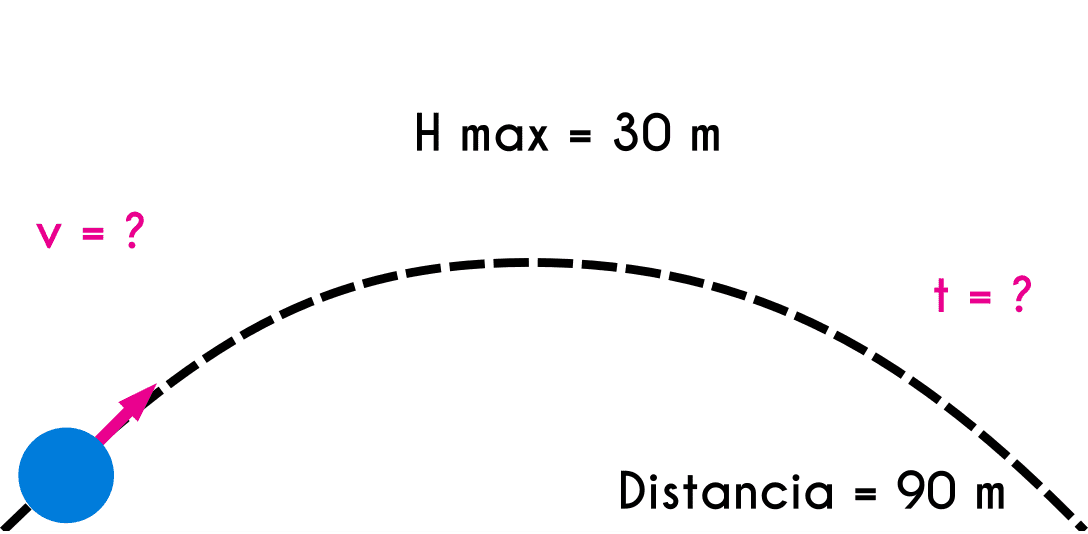
Max height = 30 mDistance = 90m t = ? Vo = ?

Knowing the max height first we are going to find the initial velocity in the y axis and then we find the time of flight.

First we clear vo_y
v_y ²= v_o - 2 * g * y
vo_y ²= v_y² - 2 * g * y
And we solve
vo_y ² = 0 - 2 * 9.8 * 30
vo_y ² = 19.6 * 30
vo_y ² = 588
vo_y = √ 588
vo_y = 24.25 m/s

Now we can find the time of flight

Write the equation and clear the time
v_y = vo_y - g * t
t max =
v_y - vo_y/-g
t max =
-24.25 - (24.25)/-9.8
t max =
-48.5/-9.8
t max = 4.95s

And last we have to find the initial velocity of the ball first we are going to find the x velocity and then find the total velocity.

First we find the x velocity
v_x = d / t
v_x = 90 / 4.95
v_x = 18.18s
And finally we find the total velocity
v = √ v_x² + vo_y²
v = √ 18.18² + 24.25²
v = √ 330.51 + 588.06
v = 30.3

Example 3: Someone hits a ball at a velocity of 40m/s, the time of flight was of 7.2 seconds, calculate the range of the ball.

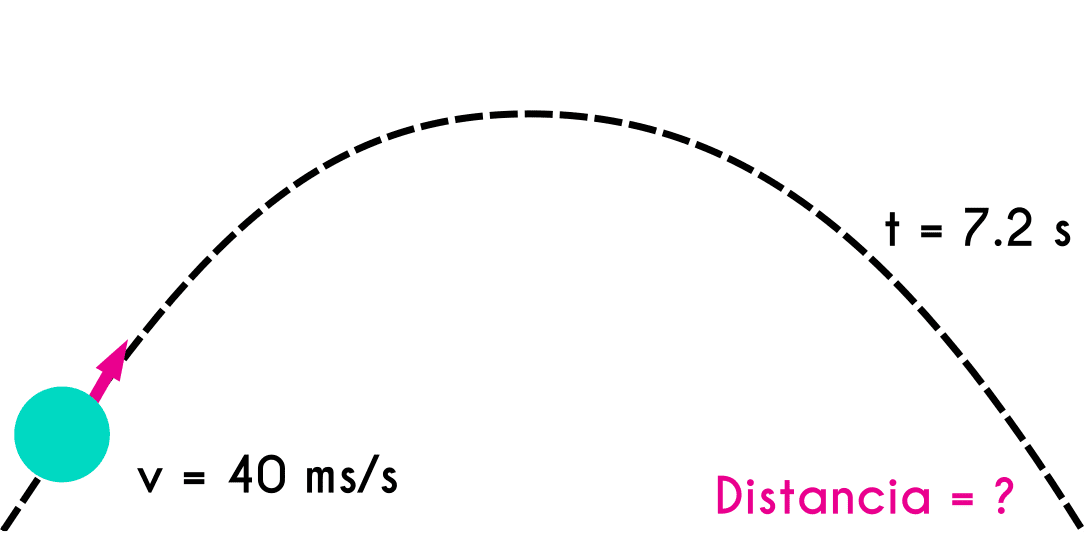
v = 40 m/s t = 7.2 s Distance = ?

In this problem we have to find a data that belongs to the x axis but we only have the time and just with this we can not find it directly, also, we can not decompose the velocity because we do not have the intial inclination angle of the ball, so here is what we are going to do.

The only data we have is the time of flight so we are going to work with it, so we are going to find the moment where the y velocity is equals to 0, and as we explained it is exactly in half of the motion, which means that is half of the time flight, so now we have the enough data to solve the problem.

We write the equation and clear voy
v_y = vo_y - g * t
vo_y = v_y + g * t
vo_y = 0 + 9.8 * 3.6
vo_y = 35.28

Now knowing the velocity on y and the total velocity we can find the velocity on x

We find velocity on x
vo² = vo_y² + v_x²
v_x² = vo² - vo_y²
v_x² = 40² - 35.28²
v_x² = 1600 - 1244.68
v_x² = 355.32
v_x = √ 355.32
v_x = 18.84 m/s

And last we find the range

d = v * t
d = 18.84 * 7.2
d = 135.64

Example 4: somebody throws an object at an initial velocity of 200m/s with an inclination of 45 degrees, calculate the time of flight and the range of the object.

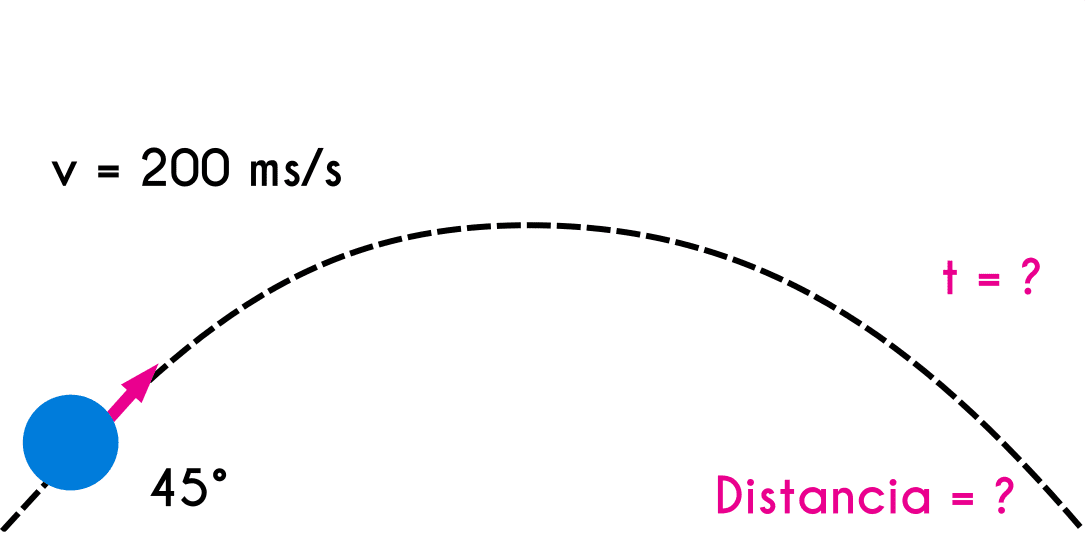
vo = 200 m/s Θ = 45° t = ? d = ?

First we are going to decompose the velocity on the axis "x" and "y"
vo_y = vo * sen(Θ)
vo_y = 200 * sen(45)
vo_y = 141.42
v_x = vo * cos(Θ)
v_x = 200 * cos(45)
v_x = 141.42

Now we can find the time of flight
v_y = vo_y - g * t
t =
v_y -vo_y/-g
t =
-141.42 - (-141.42)_y/-9.8
t =
-282.9_y/-9.8
t = 28.87

And finally we find the distance covered
d = v * t
d = 141.42 * 28.87
d = 4 828

Example 5: A ball is thrown at an initial velocity of 21m/s, if we know that it reached a 10 meters high, define the range and the time of flight.

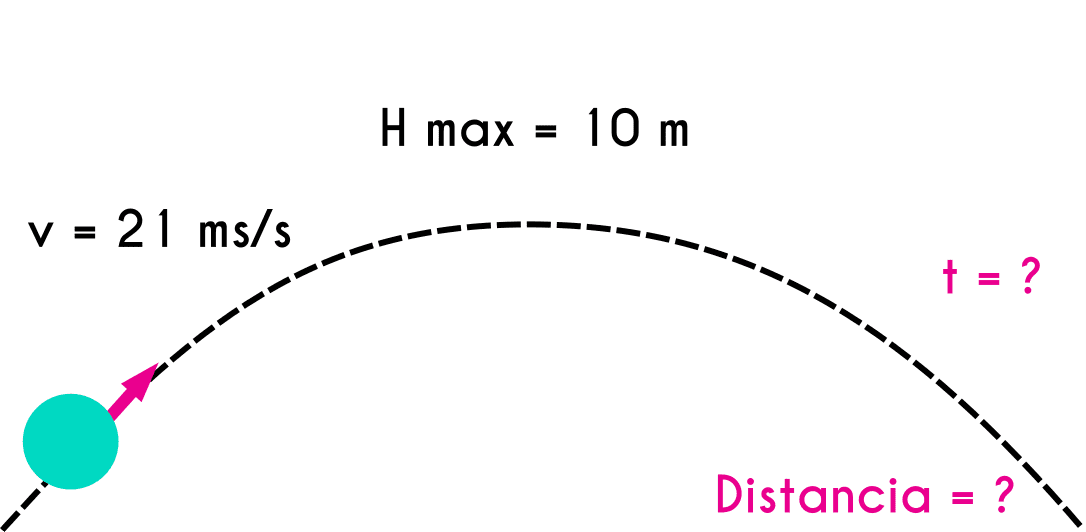
vo = 21 m/s Height max= 10 m d = ? t = ?

We find the initial velocity on y taking as reference when the velocity of the object is equals to 0 (is when the max height happens)
v_y² = vo_y² - 2 * g * y
vo_y² = v_y² - 2* g * y
vo_y² = 0² - 2(9.8)(10)
vo_y² = 196
vo_y = √196
v_y = 14

With the velocity we can now find the time of flight
v_y = vo_y - g * t
t =
v_y - vo_y/-g
t =
-14 - (-14)/-9.8
t =
28/-9.8
t = 2.86

Next we find the velocity on x
vo² = vo_y² + v_x²
v_x² = vo² - vo_y²
v_x² = 21² - 14²
v_x² = 441 - 196
v_x² = 245
v_x = √ 245
v_x = 15.64

And last we find the distance
d = v_x * t
d = 15.64 * 2.86
d = 44.73

Related articles

Constant velocity motion Uniformly accelerated motion Free fall Vertical motion Uniform circular motion Non uniform circular motion Kinematics Projectile motion calculator Uniformly accelerated motion calculator