Partes de un círculo
En este artículo se estudiarán las parte principales de un círculo, con la definición de cada una de las partes y como encontrarlas
Definición de un Círculo
Un círculo es una figura geométrica que se forma mediante una línea curvada que regresa al mismo punto donde comenzó. Aunque el círculo es un concepto fundamental en geometría, su influencia se extiende mucho más allá de esta disciplina. Incluso cuando no podemos trazar un círculo perfecto con precisión absoluta en la realidad, las operaciones y principios relacionados con los círculos tienen aplicaciones en diversas áreas del conocimiento. Por esta razón, es de vital importancia explorar en profundidad los componentes y propiedades fundamentales del círculo, ya que estos conceptos desempeñan un papel esencial en numerosas ramas del saber.
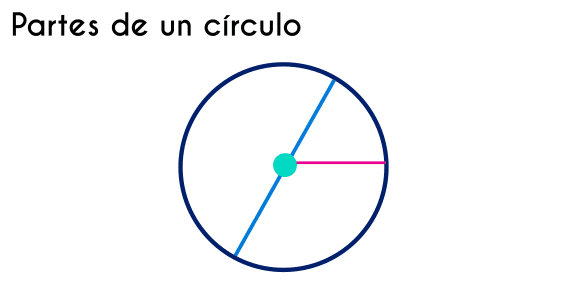
Un círculo se compone de varias partes distintivas, y cada una de ellas está interconectada, lo que significa que a partir del conocimiento de una de estas partes, es posible deducir el valor o las características de las demás, mediante el uso de las fórmulas apropiadas.
Partes de un Círculo
Las partes de un círculo no comparten las mismas dimensiones entre sí. Esto significa que si una parte del círculo tiene una longitud de "x" metros, no habrá otro círculo que tenga exactamente la misma longitud "x" en esa parte específica. Esta característica demuestra la estrecha interconexión entre cada componente del círculo, donde cualquier cambio en una parte afecta automáticamente a las demás.
Circunferencia
La circunferencia de un círculo es el perímetro del círculo, lo que significa que es la línea que abarca todo el borde o contorno del círculo. A menudo, la circunferencia puede ser confundida con el círculo en sí, y es común que se utilicen como sinónimos en algunos contextos. Sin embargo, es importante destacar que la circunferencia es específicamente la línea que rodea al círculo y no el área interior.
Propiedades adicionales de la circunferencia incluyen su simetría rotacional, lo que significa que cada punto de la circunferencia es equidistante del centro del círculo. Además, la longitud de la circunferencia se calcula utilizando fórmulas que dependen del radio o del diámetro del círculo, como Circunferencia = Diámetro * π o Circunferencia = 2 * Radio * π. Esto implica que la circunferencia es proporcional al tamaño del círculo, ya que su longitud aumentará o disminuirá en función de cambios en el radio o el diámetro del círculo. La relación entre la circunferencia y el diámetro es constante y está representada por el número π (pi), que es aproximadamente igual a 3.1416. Esta relación es un concepto fundamental en geometría y tiene aplicaciones en una amplia variedad de campos de la ciencia y la ingeniería.
- Circunferencia = diámetro * PI
- Circunferencia = 2radio * PI
Es importante tener en cuenta que no existe una circunferencia perfectamente precisa desde una perspectiva física o visual. La perfección de una circunferencia solo se puede lograr en la mente o la imaginación, ya que es prácticamente imposible dibujar, diseñar o construir una circunferencia que sea completamente perfecta en todas sus partes. Esto se debe a las limitaciones inherentes a la precisión en la representación física, donde siempre habrá pequeñas variaciones o imperfecciones en la forma de cualquier objeto circular que se materialice en el mundo real.
Centro
El centro de un círculo es un punto crucial en su estructura. Este punto se encuentra equidistante de todos los puntos de la circunferencia, lo que significa que cualquier línea trazada desde el centro hasta un punto en la circunferencia tendrá la misma longitud.
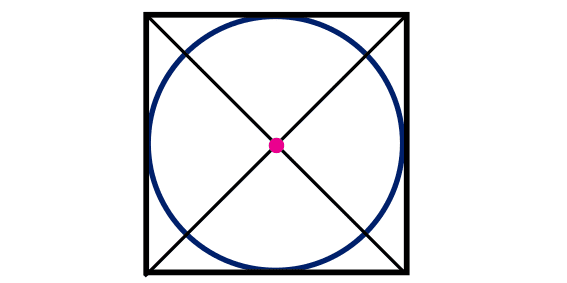
Determinar la posición exacta del centro de un círculo puede hacerse de varias formas, pero una de las técnicas más simples implica dibujar un cuadrado que enmarque al círculo. Una vez que se ha dibujado el cuadrado, trazar dos líneas diagonales desde las esquinas del cuadrado. El punto en el que estas dos líneas se cruzan será el centro del círculo.
Radio
El radio de un círculo es una línea que parte desde el centro del círculo y se extiende hacia cualquier punto en la circunferencia. En otras palabras, es como si estiraras una cuerda desde el centro del círculo hasta tocar uno de los puntos en el borde exterior. Lo interesante es que sin importar la dirección en la que traces esta línea desde el centro, siempre tendrás la misma longitud. Esto significa que si midieras la distancia desde el centro hasta cualquier punto en el círculo, obtendrás la misma medida, que llamamos el radio.
El radio es una característica fundamental del círculo y se representa comúnmente con la letra 'r'. Es importante destacar que el radio siempre es la mitad de la longitud del diámetro del círculo. Por lo tanto, si conoces el valor del diámetro, puedes calcular el radio dividiendo el diámetro entre 2. Esta relación simple entre el radio y el diámetro es esencial para comprender y resolver problemas relacionados con círculos en la geometría y otras disciplinas.
- Diametro = Circunferencia / PI
- Radio = Circunferencia / 2 PI
Diámetro
El diámetro es una línea que se extiende desde un punto en la circunferencia del círculo hasta otro punto en la circunferencia, pasando siempre por el centro del círculo. En otras palabras, es como si tomaras una cuerda larga y la colocaras de un extremo al otro del círculo de manera que pase por el punto central. Esto es importante, ya que una línea solo se considera el diámetro de un círculo si atraviesa el centro; de lo contrario, no se considera un diámetro.
El diámetro tiene una propiedad especial: divide al círculo en dos partes iguales, cada una con una medida idéntica. Esta característica lo convierte en una herramienta importante para comprender la simetría y las propiedades geométricas de los círculos. Además, el diámetro siempre es exactamente el doble de la longitud del radio del círculo. Es decir, si conoces el valor del radio, puedes encontrar el diámetro multiplicando el radio por 2.
- Diametro = 2 radio
Cuerda y arco
En contraste con elementos fijos como el radio, la circunferencia o el diámetro, las cuerdas y el arco de un círculo son componentes que varían y se adaptan según lo que se desee conocer o medir en el círculo.
Las cuerdas son segmentos de línea que conectan dos puntos en la circunferencia del círculo. Estos puntos pueden estar ubicados en cualquier lugar a lo largo del borde de la circunferencia. La longitud de una cuerda puede variar dependiendo de la distancia entre los puntos seleccionados. Las cuerdas son útiles para medir distancias en el círculo y para establecer relaciones geométricas entre diferentes puntos.
El arco, por otro lado, es una porción específica de la circunferencia que se encuentra entre dos puntos en el borde del círculo. A diferencia de las cuerdas, los arcos son una medida angular y se expresan típicamente en grados o radianes. La longitud de un arco depende de la cantidad de circunferencia que abarca y puede variar desde una pequeña fracción hasta la longitud total de la circunferencia. Los arcos se utilizan para medir ángulos en el círculo y son fundamentales en trigonometría y geometría.
PI (π)
π (pi) es un número ampliamente reconocido en el contexto de los círculos y la geometría. Se define como la relación entre la longitud de la circunferencia de un círculo y su diámetro. Aproximadamente, el valor de π es 3.1416, aunque en realidad es un número irracional, lo que significa que su representación decimal nunca se repite y nunca termina, y tiene infinitos decimales después del punto.
La presencia de π no se limita solo a los círculos. Este número especial aparece en numerosas ramas de las matemáticas y la física debido a su naturaleza única y constante. Algunos ejemplos de su relevancia incluyen:
Geometría: Como se mencionó anteriormente, π es fundamental en la geometría, ya que está directamente relacionado con las propiedades de los círculos, la medida de ángulos y las relaciones de áreas y volúmenes en formas circulares.
Trigonometría: π se utiliza en trigonometría para calcular funciones trigonométricas como el seno, el coseno y la tangente. Estas funciones son fundamentales en el estudio de triángulos y ondas, y π juega un papel clave en sus fórmulas.
Análisis Matemático: π es una constante esencial en análisis matemático, donde se utiliza en cálculos de límites, integrales y series. Aparece en numerosas identidades matemáticas y ecuaciones que son fundamentales para comprender el comportamiento de funciones y fenómenos matemáticos.
Física: En física, π se encuentra en numerosas ecuaciones que describen fenómenos naturales, como la ley de Coulomb en la electrostática, la ley de gravitación universal de Newton y las ecuaciones de ondas y oscilaciones. También se utiliza en la mecánica para describir el movimiento circular y angular.
Ingeniería y Tecnología: π se aplica en diversas disciplinas de ingeniería y tecnología, como la electrónica, la informática, la ingeniería civil y la aeronáutica, para resolver problemas relacionados con geometría, trigonometría y cálculos de diseño.
Ejercicios sobre partes de un círculo
Ejemplo 1: Encuentra la circunferencia de un círculo si el radio de este mide 5 centímetros
Datos del ejercicio 1
Radio = 5 cm Circunferencia = ?
- Se plantea la fórmula
- Circunferencia = 2 * π * Radio
- Se reemplazan los datos
- Circunferencia = 2 * π * 5 cm
- Se realizan las operaciones
- Circunferencia ≈ 31.42 cm
- Circunferencia ≈ 31.42 cm
Ejemplo 2: Encuentra el radio de un círculo sabiendo que su diámetro es de 12 centímetros
Datos del ejercicio 2
Diámetro = 12 cm Radio = ?
- Se plantea la fórmula
- Radio = Diámetro / 2
- Se reemplazan los datos
- Radio = 12 cm / 2
- Se realizan las operaciones
- Radio = 6 cm
- Radio = 6 cm
Ejemplo 3: Si la circunferencia de un círculo mide 25 centímetros, cuanto mide su diámetro?
Datos del ejercicio 3
Circunferencia = 25 cm Diámetro = ?
- Se plantea la fórmula
- Diámetro = Circunferencia / π
- Se reemplazan los datos
- Diámetro = 25 cm / π
- Se realiza la operación
- Diámetro ≈ 7.96 cm (aproximadamente)
- Diámetro ≈ 7.96 cm (aproximadamente)
Conclusión
El círculo es una figura geométrica aparentemente simple, pero su estudio detenido revela una riqueza de aplicaciones y conceptos en una amplia gama de campos. A pesar de su simplicidad aparente, el círculo se encuentra en el centro de la geometría y desempeña un papel fundamental en la ciencia y la tecnología.
Las partes de un círculo, como la circunferencia, el radio, el diámetro y más, tienen propiedades y relaciones que influyen en nuestra vida cotidiana. Ya sea en el diseño de ruedas de automóviles, la medición de distancias geodésicas (es la distancia más corta entre dos puntos en una superficie curva) o el cálculo de áreas en geometría, el círculo se presenta como una herramienta esencial.
Su presencia en campos tan diversos como la astronomía, la física, la ingeniería y la matemática demuestra su versatilidad y relevancia. Y la constante π (pi), que relaciona la circunferencia con el diámetro, se manifiesta en numerosos contextos.
Artículos relacionados