Caída libre
En este artículo se definira en que consiste el movimiento de caída libre, con las fórmulas para resolver problemas, ejermplos y ejercicios resueltos.
Definición de Caída Libre
La caída libre es un concepto fundamental en la física que se refiere al movimiento de un objeto cuando se deja caer desde cierta altura sin aplicarle ninguna fuerza inicial o velocidad. En este artículo, exploraremos en qué situaciones se considera un movimiento de caída libre, la importancia de su estudio y su relación con el famoso episodio de la manzana de Isaac Newton.
La caída libre es un fenómeno que ocurre cuando un objeto es liberado desde cierta altura y cae hacia la Tierra bajo la influencia exclusiva de la gravedad. En este contexto, es crucial destacar que la caída libre solo se manifiesta cuando no se le imprime al objeto ninguna velocidad inicial ni se le aplica ninguna fuerza adicional. Si se proporciona una velocidad inicial, estaríamos hablando de un tiro vertical en lugar de una caída libre. Este fenómeno es una variante de un movimiento rectilíneo uniformemente acelerado (MRUA), que se caracteriza por una aceleración constante debida a la gravedad.
Importancia y Aplicaciones de la Caída Libre
El estudio de la caída libre es esencial en la física y la ingeniería, ya que sienta las bases para comprender el comportamiento de los objetos en el campo gravitatorio de la Tierra. Esta comprensión es fundamental en una amplia variedad de aplicaciones, desde la física de partículas y la mecánica celeste hasta el diseño de paracaídas y sistemas de frenado en vehículos espaciales. Además, la caída libre es un concepto que desempeñó un papel clave en la revolución científica de los siglos XVII y XVIII, y su historia está intrincadamente relacionada con figuras como Isaac Newton y su famosa historia de la manzana.
Características de la Caída Libre
La caída libre es un movimiento rectilíneo uniformemente variado que ocurre únicamente a lo largo del eje vertical (eje "y"). Una condición esencial para que se considere una caída libre es que la velocidad inicial del objeto siempre debe ser igual a cero (0), mientras que la aceleración toma el valor de la gravedad local (aproximadamente 9.8 m/s^2). En condiciones ideales de caída libre, donde no hay presencia de aire u otros factores que afecten la trayectoria del objeto, este se desplaza exclusivamente a lo largo del eje "y".
Un objeto en caída libre comienza su movimiento con una velocidad inicial de 0 m/s, pero a medida que transcurre el tiempo y el objeto cae, su velocidad aumenta de manera progresiva hasta que impacta contra el suelo o cualquier objeto que se interponga en su trayectoria. Por lo tanto, a mayor altura desde la cual se deje caer un objeto, mayor será el impacto contra el suelo.
Factores a tener en cuenta en una caída libre
La trayectoria de un objeto en caída libre puede verse afectada por las masas de aire, un fenómeno también conocido como resistencia aerodinámica. Inicialmente, un objeto en caída libre se mueve únicamente verticalmente, pero debido a la presencia de masas de aire, este se puede desviar de su trayectoria, tanto vertical como horizontalmente. El grado en que afecta la resistencia aerodinámica a la trayectoria de un objeto depende de su peso; a mayor peso, menor será el efecto de las masas de aire en su trayectoria.
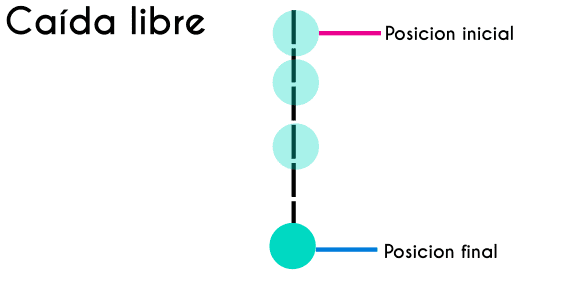
Tiro semi parabólico
Un tiro o movimiento semiparabólico es un tipo de caída libre con la diferencia de que este incluye movimiento en el eje horizontal. Este movimiento se produce cuando se lanza un objeto desde cierta altura aplicando fuerza horizontal. A pesar de que se ejerce una fuerza en el objeto, esta afecta solo al eje horizontal (eje "x"). En cambio, el eje vertical (eje "y") sigue moviéndose debido a la gravedad. Un ejemplo típico sería lanzar una flecha en línea recta desde un acantilado.
El movimiento semiparabólico constituye la segunda mitad de un movimiento parabólico. Es cuando el objeto alcanza una velocidad en el eje "y" igual a cero y comienza a descender debido a la influencia de la gravedad.
Fórmulas de caída libre
Como se mencionó anteriormente, una caída libre es un Movimiento Rectilíneo Uniformemente Variado (MRUV) con ciertas condiciones fijas, como la velocidad inicial y la gravedad. Por lo tanto, las fórmulas o ecuaciones utilizadas para resolver problemas son las mismas que en el MRUV, pero con algunas modificaciones. Las fórmulas que se presentan a continuación son las del MRUV simplificadas para reflejar las condiciones de una caída libre.
- vf = g . t
- y = 1/2g . t2
- vf2 = 2g . y
- y = ( vf /2) . t
Historia de la Caída Libre y su Impacto en la Física
La caída libre es uno de los fenómenos más antiguamente estudiados en la historia de la física. Uno de los primeros científicos en abordar este concepto fue el filósofo y científico griego Aristóteles, quien en el siglo IV a.C. sostenía que los objetos caían a una velocidad proporcional a su peso. Sin embargo, fue durante la Revolución Científica que la comprensión de la caída libre dio un salto significativo.
Uno de los hitos más notables en la historia de la caída libre es la leyenda de Isaac Newton y la famosa manzana. Aunque la historia de la manzana cayendo en la cabeza de Newton puede ser apócrifa, Newton realmente formuló la Ley de la Gravitación Universal, que proporcionó una explicación matemática precisa para el comportamiento de la gravedad y la caída de los objetos. Esta ley, publicada en su obra "Philosophiæ Naturalis Principia Mathematica" en 1687, revolucionó la comprensión de la caída libre y sentó las bases de la mecánica clásica.
A partir de la comprensión de la caída libre, se desarrollaron conceptos clave como el movimiento rectilíneo uniformemente acelerado (MRUA), que se aplican en numerosas áreas de la física y la ingeniería. Desde la dinámica de partículas hasta la física de fluidos y la ingeniería de estructuras, la caída libre sigue siendo un pilar fundamental en la física y ha influido en la evolución de la ciencia a lo largo de los siglos.
Ejemplos de la Importancia de la Caída Libre en la Práctica
El estudio de la caída libre tiene una amplia aplicación en diversas profesiones y situaciones prácticas. A continuación, se presentan algunos ejemplos que ilustran su relevancia:
- Paracaidismo: En deportes como el paracaidismo, entender la caída libre es esencial para calcular el tiempo de caída, la velocidad de apertura del paracaídas y la distancia de aterrizaje.
- Industria de la aviación: En la aviación, el estudio de la caída libre es fundamental para diseñar sistemas de seguridad, como los cinturones de seguridad y los sistemas de inflado de chalecos salvavidas.
- Construcción de edificios y puentes: Los ingenieros civiles utilizan los principios de la caída libre para calcular la resistencia de los materiales y diseñar estructuras capaces de soportar cargas en caída libre, como elevadores y ascensores.
- Física de partículas: En la investigación de partículas subatómicas, la caída libre se aplica para estudiar las trayectorias de partículas en aceleradores de partículas.
- Exploración espacial: En la exploración del espacio, el conocimiento de la caída libre es crucial para calcular órbitas y trayectorias de naves espaciales.
Estos ejemplos destacan cómo el estudio de la caída libre no solo es fundamental en la teoría física, sino que también tiene un impacto significativo en la práctica en una amplia variedad de campos y profesiones.
Ejemplos de Caída libre
A continuación unos ejemplos de movimientos que se clasifican como caída libre
- Un paracaidista que se lanza desde un helicoptero
- Una manzana que cae desde un árbol
- Dejar caer una piedra desde cierta altura
- Una gota que cae desde el techo de una casa
- Un vaso que cae desde una mesa
Ejercicios de caída libre
Ejercicio 1: una persona deja caer una piedra desde una altura de 1.75 metros ¿Cuánto tardo la piedra en tocar el suelo?
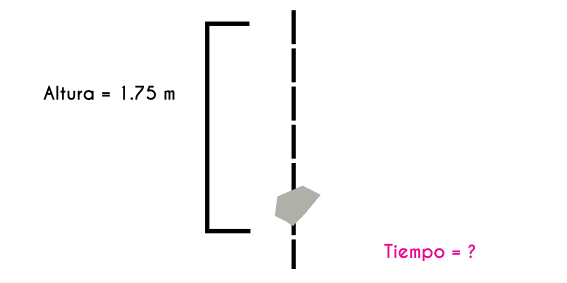
y = 1.75 m/s T = ?
- Se plantea la ecuación
- y = -1/2g * t2
- Se despeja el tiempo
-
t 2 =
y1/2 g
- Se cambian las variables
-
t 2 =
1.751/2 (9.8)
- Se realizan las operaciones
-
t 2 =
1.754.9
- t2 = 0.357
- t = √ 0.357
- t = 0.597
Ejercicio 2: Si se deja caer una bola de demolición desde una altura de 10 metros ¿Cuál será la velocidad con la que impactará la bola al suelo?
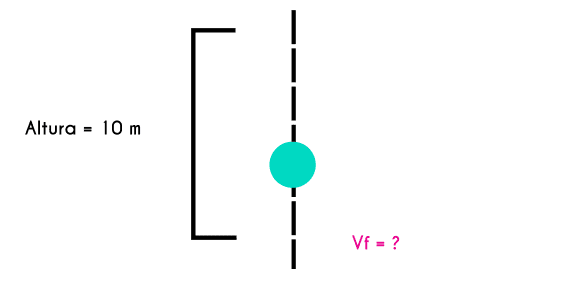
y = 10 m Vf = ?
- Se plantea la fórmula
- vf2 = 2g * y
- Se cambian las variables
- vf2 = 2(9.8) * 10
- Se realizan las operaciones
- vf2 = 196
- vf = √ 196
- vf = 14 m/s
Ejercicio 3: Un vaso necesita un impacto mínimo de 3.7 m/s, si este vaso cae desde una mesa de 0.8 metros de altura ¿Se quebró el vaso al golpear el suelo?
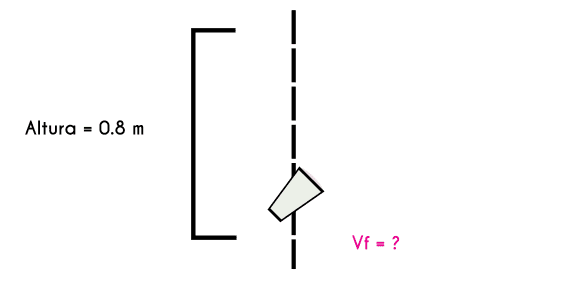
Vf = 3.7 m/s y = 0.8 m/s
- Se plantea la ecuación
- vf2 = 2g * y
- Se cambian las variables
- vf2 = 2(9.8) * 0.8
- Se realizan las operaciones
- vf2 = 19.6 * 0.8
- vf2 = 15.68
- vf = √ 15.68
- vf = 3.96 m/s
- Por lo que el vaso si se quebró
Ejercicio 4: Se deja caer un balón de baloncesto desde la azotea de un edificio de 44 metros si se desea hacer una canasta en un aro de baloncesto que está a 3 metros de altura ¿Cuánto tiempo tardara la bola en alcanzar el aro?
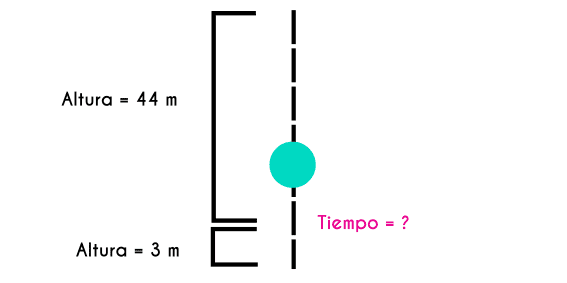
y = 44 m - 3m T = ?
- Primero se calcula la distancia que tendrá que recorrer la bola
- y = altura edificio - altura aro
- y = 44m - 3m
- y = 41m
- luego se plantea la ecuación
- y = 1/2 * g * t2
- Se despeja el tiempo
- t2 = y / (1/2 * g)
- Se cambian las variables
- t2 = 41 / (1/2 * 9.8 m/s)
- Se realizan las operaciones
- t2 = 41 / 4.6
- t2 = 8.91
- t = √ 8.91
- t = 2.98 s
Ejercicio 5: Un mango cae desde una rama de un árbol que está a 5 metros de altura, si justo bajo el mango se encuentra un señor de 1.78m de alto ¿A qué velocidad le cae el mango al señor?
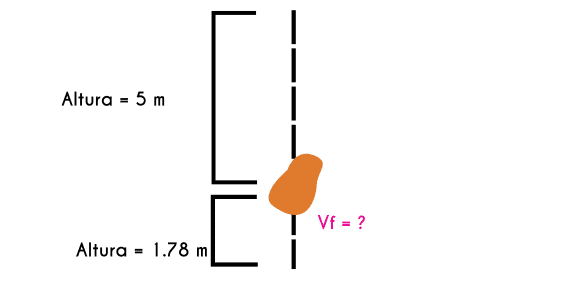
y = 5 m - 1.78m Vf = ?
- Primero se calcula la altura que caerá
- y = altura rama - altura señor
- y = 5m - 1.78m
- y = 3.22m
- luego se plantea la ecuación
- vf2 = 2g * y
- Se cambian las variables
- vf2 = 2(9.8) * 3.22
- Se realizan las operaciones
- vf2 = 19.6 * 3.22
- vf2 = 63.11
- vf = √ 63.11
- vf = 7.94 m/s
Ejercicio 6: Una pelota se deja caer desde una altura de 2.5 metros. ¿Cuánto tiempo tarda en llegar al suelo?
y = 2.5 m t = ?
- Se plantea la ecuación
- y = -1/2g * t2
- Se despeja el tiempo
-
t 2 =
y1/2 g
- Se cambian las variables
-
t 2 =
2.51/2 (9.8)
- Se realizan las operaciones
-
t 2 =
2.54.9
- t2 ≈ 0.5102
- t ≈ √0.5102
- t ≈ 0.714 segundos
Ejercicio 7: Un objeto cae desde una altura de 30 metros. ¿Cuál será su velocidad cuando toque el suelo?
y = 30 m vf = ?
- Se plantea la fórmula
- vf2 = 2gy
- Se cambian las variables
- vf2 = 2(9.8) * 30
- Se realizan las operaciones
- vf2 = 588
- vf ≈ √588
- vf ≈ 24.25 m/s
Conclusión
La caída libre es un fenómeno fundamental en la física que ha sido estudiado a lo largo de la historia y ha tenido un impacto significativo en la evolución de esta ciencia. Desde los tiempos de Aristóteles hasta los experimentos de Newton, la comprensión de la caída libre ha revolucionado nuestra percepción de la gravedad y el movimiento de los objetos.
A través de ejemplos resueltos, hemos demostrado cómo aplicar las ecuaciones de la caída libre para resolver problemas prácticos, desde calcular el tiempo de caída hasta determinar la velocidad de impacto de un objeto.
Además, hemos destacado la importancia de la caída libre en diversas profesiones y situaciones, desde el paracaidismo hasta la ingeniería y la investigación espacial. Su relevancia se extiende mucho más allá de la teoría física, influyendo en numerosas aplicaciones prácticas.
En resumen, la caída libre es un concepto clave que nos permite comprender cómo los objetos se mueven bajo la influencia de la gravedad. Su historia rica y su aplicación en la vida cotidiana subrayan su importancia en el mundo de la física y la ciencia en general.
Artículos relacionados