The Pythagorean Theorem explained with Examples

This article will be about the definition of the Pythagorean theorem, how to use it, when to use it, with formulas and examples.

Definition of the Pythagorean theorem

The Pythagorean theorem is perhaps the most famous theorem that exists, this theorem is an equation that allows us to find any side of a right triangle (a triangle that has one angle of 90°) as long as we know the length of the other two sides of the triangle. The Pythagorean theorem states that: “In a right triangle, the hypotenuse squared will be equals to the sum of the two legs”. Although the definition of this theorem is set to find the hypotenuse based on the length of the legs, we can easily find also the legs by just clearing the variable we need to find.

Reminder about the names of the sides of a right triangle: In a triangle that has an angle of 90°, it is not usual to name the sides of the triangle by letters like A, B, C, etc., but we name them by “hypotenuse” and “legs”, we call hypotenuse to the longest side of the triangle, this will always be in the opposite side to the 90° angle, and the other 2 sides are called “legs”, this can be differentiated by a letter, like “leg a” and “leg b”.

Pythagorean theorem

The Pythagorean theorem is only used when we want to focus only on the sides of the triangle, because this theorem does not involve any angle.

This theorem is used mainly in vectors, this is because when we have a vector it is really easy to find a right triangle based on a vector, where the vector itself is the hypotenuse of the triangle, while the legs are the components “x” and “y” of the vector. In general the Pythagorean theorem is use to find the resultant vector when we have its components.

To add, subtract, multiply and divide vectors, normally the vectors are decomposed, and then we work only with its components, because it makes the work more simple, and then when we make the operations with the components, we get the components of the resultant vector. And then is when we use the Pythagorean theorem, to find the value of the resultant vector.

Both, Pythagorean theorem and trigonometric ratios complete each other for many branches in mathematics and physics, the difference between these 2 is that the trigonometric ratios does work with sides and angles, while the Pythagorean theorem only works with sides.

Formula of the Pythagorean theorem

The Pythagorean theorem is actually only one equation or formula, but by clearing the equation for every variable the results are three different equation one for each side of the triangle. The variables used in the theorem are A, B and C, where C is commonly use for representing the hypotenuse and A and B represents the legs of the triangle.

  • Pythagorean theorem
  • C2 = B2 + A2
  • Equation with the C solved
  • C = √B2 + A2
  • Equation to find a leg
  • A2 = C2 - B2
  • Equation with a leg solved
  • A = √C2 - B2

Examples of the Pythagorean theorem

Example 1: A triangle has a hypotenuse that is 30 meters long, if we know that one of the legs is 12 meters long, calculate the length of the other leg

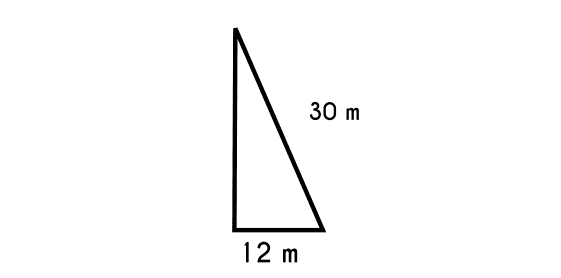
Example 1 of the pythagorean theorem

Example data

Hypotenuse C = 30mleg A = 12leg B = ?

  • First we write the equation
  • B2 = C2 - A2
  • B = √ C2 - A2
  • Then we change the data and solve.
  • B = √ 302 - 122
  • B = √ 900 - 144
  • B = √ 756
  • B = 27.49

Example 2: The hypotenuse of a triangle is 35.2 centimeters long and one of its legs is 22 centimeters long, knowing this, find the length of the other leg.

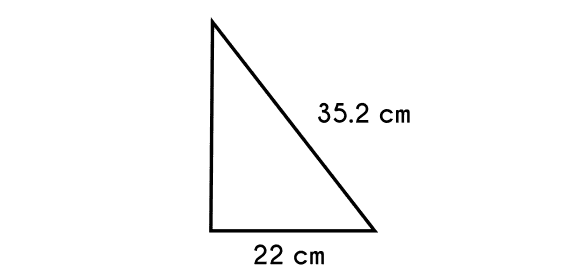
Example 2 of the pythagorean theorem

Example data:

Hypotenuse C = 35.2cmleg A = 22cmleg B = ?

  • First write the theorem
  • B2 = C2 - A2
  • B = √ C2 - A2
  • Then change the data and solve
  • B = √ 35.22 - 222
  • B = √ 1226.4 - 484
  • B = √ 742.4
  • B = 27.25

Example 3: if the two legs of a right triangle are 41.2 centimeters long, ¿What is the length of the hypotenuse?

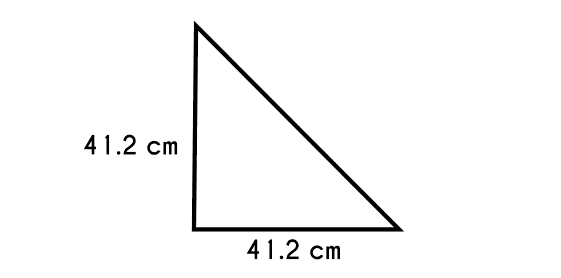
Example 3 of the Pythagorean theorem

Example data:

Leg A = 41.2cmLeg B = 41.2cmHypotenuse C = ?

  • Write the equation
  • C2 = A2 + B2
  • C = √ A2 + B2
  • And solve the operations
  • C = √ 41.22 + 41.22
  • C = √ 16097.44 + 1687.44
  • C = √ 3394.88
  • B = 58.27

Example 4: ¿What is the length of a leg if we know that the hypotenuse is 105 cm long, and the other leg is half the length of the hypotenuse?

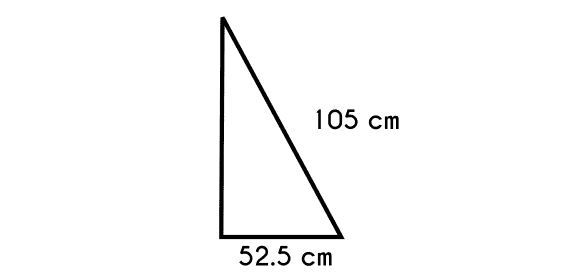
Example 4 of the Pythagorean theorem

Example data:

Hypotenuse C = 105 cmLeg A = 52.5cmLeg B = ?

  • First, write the formula
  • B2 = C2 - A2
  • B = √ C2 - A2
  • And then change the data and solve the operations
  • B = √ 1052 - 52.52
  • B = √ 11025 - 2756.25
  • B = √ 8268.75
  • B = 90.93

Example 5: Calculate the hipotenuse of a right triangle that has a 20cm leg, and a 37cm leg.

Example 5 of the pythagorean theorem

Example data:

Leg A = 20cmLeg B = 37cmHypotenuse C = ?

  • First we write the theorem
  • C2 = A2 + B2
  • C = √ A2 + B2
  • And we change the data and solve
  • C = √ 202 + 372
  • C = √ 400 + 1369
  • C = √ 1769
  • B = 42.05

Example 6: Find the value of a the other leg of a triangle if we know that it has an hypotenuse of 30cm long and a leg of 5cm long.

Example 6 of the pythagorean theorem

Example data:

Hypotenuse C = 30 cmLeg A = 5cmLeg B = ?

  • First we write the equation
  • B2 = C2 - A2
  • B = √ C2 - A2
  • And then we solve
  • B = √ 302 - 52
  • B = √ 875
  • B = 29.58

Example 7: A man is on a tree that is 3 meters long, if another man is 4 meters away on the ground, define the distance between the two.

Example 7 of the pythagorean theorem

Example data:

Leg A = 4 mLeg B = 3 mHypotenuse C = ?

  • First we write the formula
  • C2 = A2 + B2
  • C = √ A2 + B2
  • And then we solve
  • C = √ 42 + 32
  • C = √ 25
  • B = 5

Example 8: two men start from the same point at the same time, one of them started walking north, and he advanced 2km, meanwhile the other man started walking east and he advanced 1.7k, define the distance between the 2 at the end of their walks.

Example 8 of the pythagorean theorem

Example data:

Leg A = 2kmLeg B = 1.7kmHypotenuse C = ?

  • We write the formula to find the hypotenuse
  • C2 = A2 + B2
  • C = √ A2 + B2
  • And then we solve
  • C = √ 22 + 1.72
  • C = √ 6.84
  • B = 2.62

Example 9: if we know that an object moves at 2m/s on the x axis, and 3m/s on the y axis, ¿At what resultant velocity is it moving?

Example 9 of the pythagorean theorem

Example data:

Leg A = 2 m/sLeg B = 3 m/sHypotenuse C = ?

  • First, write the formula to find the hypotenuse
  • C2 = A2 + B2
  • C = √ A2 + B2
  • And then we solve the operations
  • C = √ 22 + 32
  • C = √ 13
  • B = 3.6

Example 10: A model is at on top of a wall that is 3 meters tall, if her and the photographer are 8 meters apart, and the photographer is on the ground, calculate the distance between the photographer and the wall

Example 10 of the pythagorean theorem

Example data:

Hypotenuse C = 8 mLeg A = 3 mLeg B = ?

  • First we write the equation to find a leg
  • B2 = C2 - A2
  • B = √ C2 - A2
  • And change the data, and solve
  • B = √ 82 - 32
  • B = √ 55
  • B = 7.42

Related articles

Trigonometric ratios Special right triangles