The Sines law, with examples

This article will be about The sines law, how to use this law with solved examples.

Theory of the sines law

The sines law is an equation that is in general applied in oblique triangles (triangles that does not have a 90° angle), this law is used to calculate both sides and angles of an oblique triangle. The law of the sines is mainly use in oblique triangles, but it can also be used in right triangles, but it is more recommended to use the theorems and equations that are specially for right triangles.

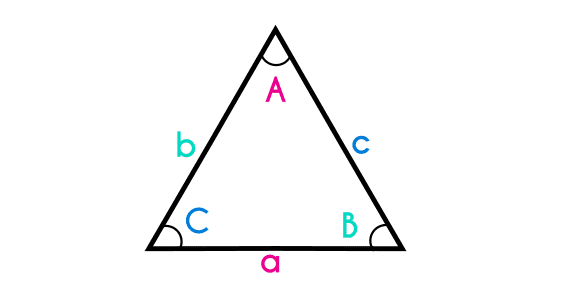
Law of the sines

The sines law establishes a relation between the sides and their opposite angles, where each side is named the same way as its opposite angle but in lower case.

The sines law is formed by three parts, one for each pair of side and angle, but to solve problems with this law we only use 2 parts at a time, but if we apply the law multiple times, we would be using the whole equation, but not at once.

Formula

  • a/sen(A)
    =
    b/sen(B)
    =
    c/sen(C)
  • ó
  • sen(A)/a
    =
    sen(B)/b
    =
    sen(C)/c

As we can see above this law equals the divisions of the sides between the angles and vice versa, no matter if the division is side/angle or angle/side, as long as every part is written the same way. The angles are named by an upper case (normally A, B and C) and the sides are named with the same letter as their opposite side but in lowercase.

To find the sides and angles of a triangle we just have to know an angle and its opposite side, and another variable, this could be an angle or a side, so to make use of this law we must know a complete part and any extra variable of the other 2 parts, so what we have to do is clear the variable we do not now and solve.

Examples of the sines law

Example 1: A triangle has a side that is 45cm long and the opposite angle to this side has an inclination of 110°, if we know that the other angle (A) has an inclination of 33 degrees, find the opposite side to this angle (a).

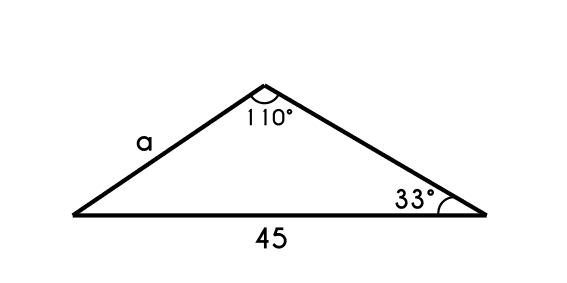
Example 1 of the sines law
  • First we write the formula
  • a/sen(A)
    =
    b/sen(B)
  • Now we replace the data
  • 45/sen(110)
    =
    a/sen(33)
  • Now we clear "a"
  • 45 * sen(33)/sen(110)
    = a
  • a = 26.08

Example 2: There is a triangle that has an angle of 45 degrees, if we now that the opposite side to this angle is of 12cm, and other of the sides (c) is of 10cm, what is the opposite angle to this (C).

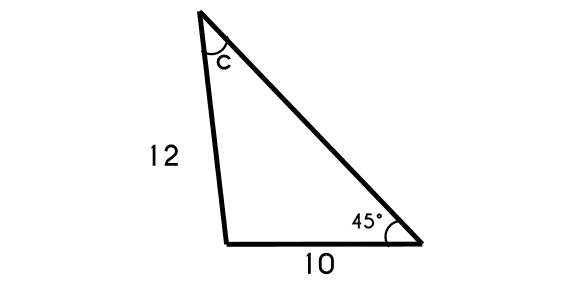
Example 2 of the sines law
  • We write the part of the formula
  • a/sen(A)
    =
    c/sen(C)
  • Now we write the data in the formula
  • 12/sen(45)
    =
    10/sen(c)
  • And last we solve C
  • C = sen-1 (
    sen(45) * 10/12
    )
  • C = 36.1

Example 3: A triangle has a side of 25 cm, and its opposite angle is of 20°, if this triangle also have a 35cm side (d), calculate the opposite angle to this side (D)

Example 3 of the sines law
  • We write the formula
  • a/sen(A)
    =
    d/sen(D)
  • Now replace the data in the formula
  • 25/sen(20)
    =
    35/sen(D)
  • And now we clear D
  • D = sen-1 (
    sen(20) * 35/25
    )
  • D = 28.61

Example 4: If there is a triangle that has an 86° angle which opposite side is of 100cm, and we know that other side of the triangle is of 45cm (h), find the opposite angle to this side (H).

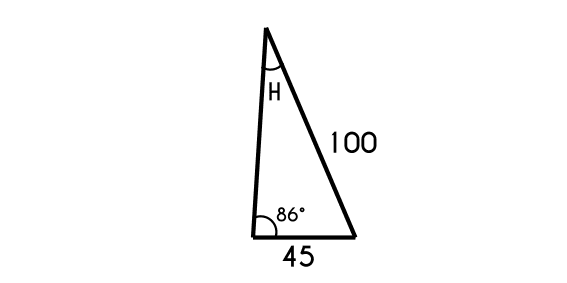
Example 4 of the sines law
  • We write a part of the equation
  • a/sen(A)
    =
    h/sen(H)
  • Now we place the data
  • 100/sen(86)
    =
    45/sen(H)
  • And solve H
  • H = sen-1 (
    sen(86) * 45/100
    )
  • H = 26.67

Example 5: If we have a triangle that has a 50cm side and its opposite anlge is of 30°, calculate the opposite side (b) to the 60° angle (B).

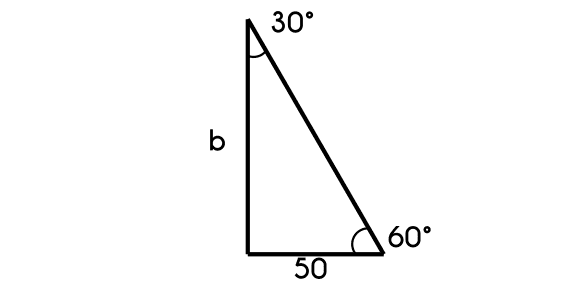
Example 5 of the sines law
  • We write the formula
  • a/sen(A)
    =
    b/sen(B)
  • Replace the data
  • 50/sen(30)
    =
    b/sen(60)
  • Clear "b" and solve
  • b =
    50 * sen(60)/sen(30)
  • b = 86.6

Related articles

Trigonometric ratios Special right triangles Pythagorean theorem