The law of the cosines, definition, formula and examples.

This article will be about The cosines law, definition, the formula to solve problems, with solved examples.

The law of the cosines is a formula that is used to determine the sides and angles of any type of triangles, but this law is mainly use in oblique triangles (triangles with a 90° angle), because for right triangles there are specifics theorems and ratios to work with.

Law of the cosines

There are two situations where we can make use of the cosines law, one of them is when we have the 3 sides of the triangle, and the other one is when we have 2 sides of the triangle and we know the angle that form these two sides, only in these two scenarios is where we can use this formula.

When we use the cosines law we are going to find one data at a time (either an angle or a side), so it is necessary to apply the law multiple times to solve the full triangle.

Formula of the cosines law

The cosines law is only one, but in the section below we show 3 variants of the formula, the only thing that changes is the position of the variables to show that we can find any angle or side.

  • c2 = a2 + b2 - 2 * a * b * cos(C)
  • b2 = a2 + c2 - 2 * a * c * cos(B)
  • a2 = b2 + c2 - 2 * b* c * cos(A)

In the cosines law is very common to clear a variable, so it is important to know how to clear variables, however, in the examples made below in this article, there are examples of how to clear a variable..

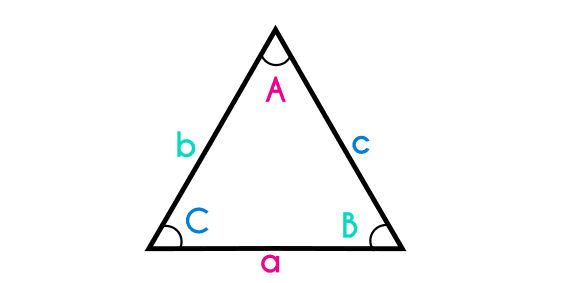
Name of angles and sides to use the law of the cosines

Something that is important to remember is the way the sides and angles are called, in general both angles and sides of a triangle are named by the first 3 letters of the alphabet, both sides and angles are named with the same three letters, the difference is that the sides are named with lower cases (a, b, c) and the angles are written with upper cases (A, B, C) where the angles of the triangle are named the same way as their opposite side.

The previous thing is the general way to name the parts of a triangle, but there are people that use a different way to name these parts, but it does not mean that it is wrong, but this way is the simplest.

Examples of the law of the cosines

Example 1: There is a triangle that has an (a) side that is 30 meters, and other side (b) is of 40 meters, if the angle that these two sides form is of 23°(C), find the longitude of the remaining side (d).

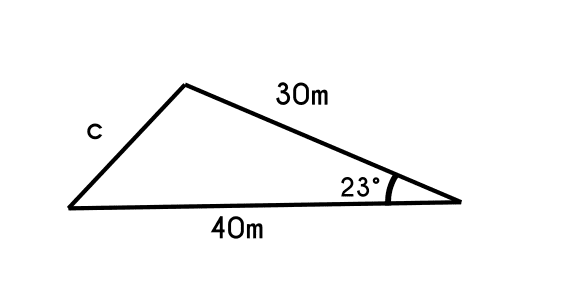
Example 1 of the law of the cosines
  • First we have to write the formula
  • c2 = a2 + b2 - 2 * a * b * cos(C)
  • In this case is not necessary to clear any variable, so we only change the data
  • c2 = 302 + 402 - 2 * 30 * 40 * cos(23°)
  • And solve
  • c2 = 2 500 - 2 400 * cos(23°)
  • c2 = 2 500 - 2209.21
  • c2 = 290.79
  • c = √290.79
  • c = 17.05

Example 2: There is a triangle that has an angle (A) of 45°, if we know that the sides that form this angle are of 12 cm (b) and 22cm (c), calculate the other side of the triangle (a).

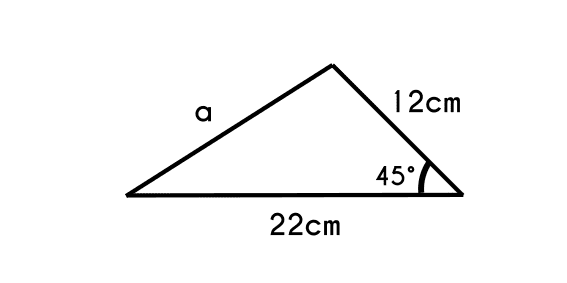
Example 2 of the law of the cosines
  • We write the cosines law
  • a2 = b2 + c2 - 2 * b * c * cos(A)
  • Change the data and solve
  • a2 = 122 + 222 - 2 * 12 * 22 * cos(45)
  • a2 = 144 + 484 - 373.35
  • a2 = 254.65
  • a = √254.65
  • a = 15.96

Example 3: Calculate the angle C of a triangle that has the following sides: a=20c, b=23cm and c=10cm.

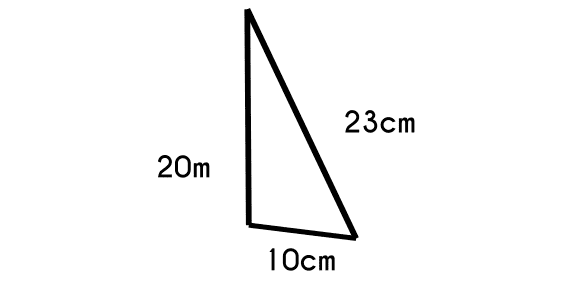
Example 3 of the law of the cosines
  • We write the equation
  • c2 = a2 + b2 - 2 * a * b * cos(C)
  • Now we clear cos(C)
  • c2 = a2 + b2 - ( 2 * a * b * cos(C) )
  • c2 - a2 - b2 = - ( 2 * a * b * cos(C) )
  • c2 - a2 - b2 = (- 2 * a * b ) * cos(C)
  • cos(C) =
    c2 - a2 - b2/- 2 * a * b
  • And replace the data and solve
  • cos(C) =
    102 - 202 - 232/- 2 * 20 * 23
  • cos(C) =
    100 - 400 - 529/- 920
  • cos(C) =
    -829/- 920
  • cos(C) = 0.901
  • C = cos-1(0.901)
  • c = 25.71

Example 4: What is the length of the remaining side (g) of a triangle that has the sides (e) and (f) of 30m each and the angle these two sides form (G) is of 45 degrees.

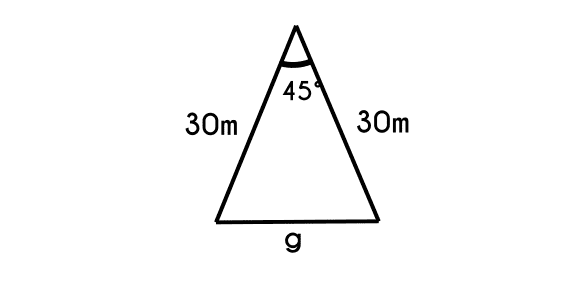
Example 4 of the law of the cosines
  • Write the equation
  • g2 = e2 + f2 - 2 * e * f * cos(G)
  • Now change the data and solve
  • g2 = 302 + 302 - 2 * 30 * 30 * cos(45)
  • g2 = 1 800 -1 272.79
  • g2 = 1 800 -1 272.79
  • g = √ 527.21
  • g = 22.96

Example 5: Find every angle of a triangle that has the following sides: a=40cm, b=50cm and c=44cm.

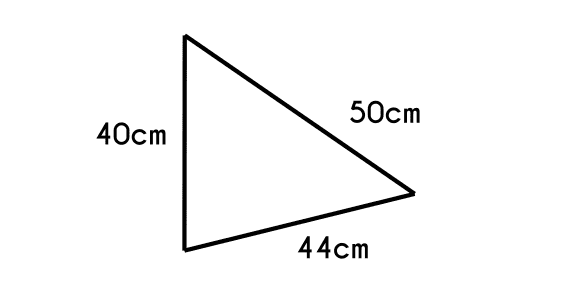
Example 5 of the law of the cosines

First we are going to find the C angle

  • Write the equation
  • c2 = a2 + b2 - 2 * a * b * cos(C)
  • Now we clear(C)
  • c2 = a2 + b2 - ( 2 * a * b * cos(C) )
  • c2 - a2 - b2 = - ( 2 * a * b * cos(C) )
  • c2 - a2 - b2 = (- 2 * a * b ) * cos(C)
  • cos(C) =
    c2 - a2 - b2/- 2 * a * b
  • Change the data and solve
  • cos(C) =
    442 - 402 - 502/- 2 * 40 * 50
  • cos(C) =
    1 936 - 1 600 - 2 500/- 4 000
  • cos(C) =
    -2 164/- 4 000
  • cos(C) = 0.541
  • C = cos-10.541
  • C = 57.25

Now we find the angle B

  • We make the same steps as in the previous angle
  • cos(B) =
    b2 - a2 - c2/- 2 * a * c
  • Change the data
  • cos(B) =
    502 - 402 - 442/- 2 * 40 * 44
  • cos(B) =
    2 500 - 1 600 - 1936/- 3 520
  • cos(B) =
    -1 036/- 3 520
  • cos(B) = 0.2943
  • B = cos-10.2943
  • B = 72.88

And last we find the angle A: we could do it using the law of the cosines, but we can also use the property of the triangles that says that the the sum of the three angles is equals to 180, so we are going to subtract to 180 the sum of the two angles we have.

  • A + B + C = 180
  • A + 57.25 + 72.88 = 180
  • A = 180 - 57.25 - 72.88
  • A = 49.87

Artículos relacionados

Trigonometric ratios Special right triangles Pythagorean theorem Law of the sines