The conditional probability - Definition and Examples
This article will be about The conditional probability, the formula, how to apply this probability with examples.
Conditional probability
The conditional probability is used when there is a probability that an outcome will occur knowing that another outcome already happened previously, this means that most of the problems where we are going to use the conditional probability will be written the following way: “¿What is the probability that the outcome ‘A’ happens, knowing that the outcome B already happened?” or “What is the probability of A given that B happened”.
To understand better how does the conditional probability works we are going to demonstrate it with a Venn diagram, as we said before, this probability is useful when there are 2 outcomes, supposing that this are “A” and “B” and what we want to find the probability of an outcome to happen knowing that the other one already happened. It is important to say that we do not want to find A intersection B (AnB), but we are looking for the probability of “A” taking as reference everything that has to do with “B”, including here (AnB).

For example, If both “A” and “B” have the same chances of happening and the probability of both of them to happen at the same time is 25%, what we are looking for with the conditional probability is the probability of “A” when “B” already happened, the answer to this is not 25%, because this 25% represents when the two happen at the same time and what we want to find is that first “B” happens and from that find the probability of “A”.
Example of the conditional probability
If the previous explanation was not that clear, we are going to focus in the next example: There is a belief in most of the youth and adults that the teenagers that are good students in general are bad for practicing sports, and that the teenagers that are good in sports are bad in school, based on this belief a school made a study about it and the results where the following: 30% of the students are good at school, while 20% of the students are good at sports, but there is also a short 5% of the students that are good at sports and are good students. This example could be represented in a Venn diagram: D=good students, E=good at sports.
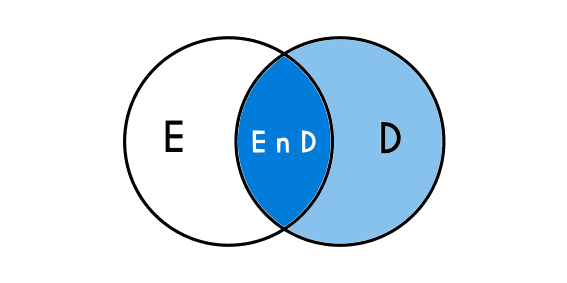
Now, if based on this data we ask ¿What is the probability that a student that is a good student is also good at sports? Then we would have to use conditional probability. The answer to the previous question is not 5% because 5% is the percentage of students that are good at both, but the objective here is that a good student is also a good athlete.
Conditional probability formula
In this formula it does not matter if we use percentages or a probability between 0 and 1, at the end the answer will be exactly the same because it uses proportions, but to obtain the results in percentage we have to multiply the answer by 100%.
- Formula of the conditional probability
- p(a | b) = p(a n b)p(b)
- Formula of the conditional probability in percentage
- p(a | b) = p(a n b)p(b)* 100%
Examples of the conditional probability
Example 1: we are going to solve the example proposed previously: if 30% are good students and 20% are good in sports and only a 5% are good at both, find the probability that a good sportman is also a good student.
st = good students sp = good at sports
- p(st | sp) = p(st n sp)p(sp)
- p(st | sp) = 5%20%
- p(st | sp) = 0.25 * 100%
- p(st | sp) = 25%
Example 2: In an aquarium there are fishes of various colors and sizes, if we know that 30% of the fishes are red and 42% of the fishes are big and we also know that 20% of the fishes are both red a big ¿What is the probability that when we pick a big fish this is also red?
r = red fishes b = big fishes
- p(r | b) = p(r n b)p(b)
- p(r | b) = 20%42%
- p(r | b) = 0.4762 * 100%
- p(r | b) = 47.62%
Example 3: we know that 20% of families of a country have at least on vehicle and 70% of the families have at least 2 children and we also know that 19% of the families have both vehicles and at least 2 children ¿what is the probability that a family that have a car have 2 kids or more?
2c = two children or more v = have a vehicle
- p(2c | v) = p(2c n v)p(v)
- p(2c | v) = 19%20%
- p(2c | v) = 0.95 * 100%
- p(2c | v) = 95%
Example 4: In a dog pound there are 50% of hairy dogs and 10% of white dogs, if we know that 2% of the dogs are hairy and white ¿What is the probability that a hairy dog is also white?
w = white dog h = hairy dog
- p(w | h) = p(w n h)p(h)
- p(w | h) = 2%50%
- p(w | h) = 0.04 * 100%
- p(w | h) = 4%
Example 5: In a company there is a 3% of the employees that are green eyed and a 20% of the workers have curly hair, if we know that 1% of the workers have green eyes and curly hair ¿What is the probability that a person with curly hair has also green eyes?
g = green eyes c = curly hair
- p(g | c) = p(g n c)p(c)
- p(g | c) = 1%20%
- p(g | c) = 0.05
- p(g | c) = 5%